Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики двумерных случайных величин.Содержание книги
Поиск на нашем сайте
Для одномерной случайной величины числовые характеристики представляют собой начальный и центральный моменты, причем наиболее существенными из них являются Для двумерной случайной величины так же существуют начальный и центральный моменты. Начальный момент порядка k, l - Центральный момент порядка k, l - Запишем формулы для вычисления этих моментов. Если случайная величина дискретная
Центральный момент Если же двумерная случайная величина непрерывна, то моменты вычисляются следующим образом:
Наиболее важными из этих моментов являются:
Особое место среди моментов играет смешанный второй центральный момент.
который обозначается Теорема. Если случайные величины X и Y независимы, то корреляционный момент равен 0. Доказательство.
Замечание: обратное утверждение, что если корреляционный момент равен 0, то случайные величины независимы – неверно. Можно лишь утверждать, что между этими случайными величинами отсутствует линейная связь. Дело в том, что может быть и нелинейная связь. Часто вместо корреляционного момента рассматривают нормированную величину, так называемый коэффициент корреляции
Этот коэффициент удовлетворяет условию
15. Основные понятия МАТЕМАТИЧЕСКой СТАТИСТИКи Математическая статистика – наука, занимающаяся установление закономерностей которым подчинены массовые однородные случайные явления. Перед математической статистикой стоят две задачи: правильно указать способы сбора информации; правильно указать способы анализа и обработки информации. Основные понятия математической статистики Пусть требуется изучить совокупность N однородных объектов относительно некоторого признака. Можно поступить двояко: произвести сплошное обследование (обследовать каждый объект относительно этого признака) или мы можем взять некоторую часть объектов, исследовать их и полученные результаты распространить на всю совокупность. Выборка – обследуемые объекты. Генеральная совокупность - вся совокупность объектов.. Объем выборки – число объектов в выборке. Существуют разные виды выборки: повторная, если объект после исследования возвращается в генеральную совокупность. не повторная, если объект не возвращается в генеральную совокупность. На практике, как правило, пользуются бесповторной выборкой. Выборка должна достаточно объективно отражать все особенности исследуемых объектов. Способы отбора. Простой случайный отбор – объекты извлекаются по одному из всей генеральной совокупности. Осуществить такой отбор можно пользуясь таблицами или датчиками случайных чисел. Типический отбор – объекты отбирают не из всей генеральной совокупность, а из некоторой ее части. Пример: Изделия изготавливают на нескольких станках, а проверяют изделия с одного станка. Серийный отбор – объекты отбирают из генеральной совокупности сериями (пачками). Пример: Выпускают лампочки и проверяют сразу ящик. Статистический ряд. Пусть из генеральной совокупности извлечена выборка объема n, причем значение
Обычно эти значения располагают в порядке возрастания и записывают в виде таблицы. - значение вариантов - частоты - относительные частоты
Размах выборки – разность Такой рая – статистический вариационный ряд. Однако если объем выборки очень большой, то в этом случае вместо статистического ряда составляют интервальный статистический ряд. Для этого всю выборку разбивают на K интервалов при помощи формулы
Наряду с интервальным рядом пользуются расширенным интервальным рядом.
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.87 (0.005 с.) |

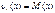 и
и 

 .
. ,
,  , а
, а  , то начальный момент
, то начальный момент .
.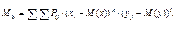
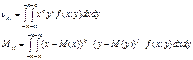
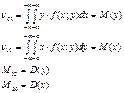
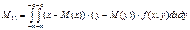 ,
,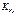 и называется корреляционным моментом. Этот момент служит для характеристики зависимости между случайными величинами X и Y.
и называется корреляционным моментом. Этот момент служит для характеристики зависимости между случайными величинами X и Y.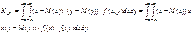

 .
. . Он точно также как и
. Он точно также как и  служит для характеристики зависимости случайных величин.
служит для характеристики зависимости случайных величин.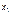 наблюдалось
наблюдалось  раз,
раз, 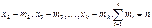 . Значения
. Значения 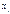 - варианты.
- варианты.

 . Составляют интервалы:
. Составляют интервалы:


 - число – вариант X значений, которые попали в i-ый интервал.
- число – вариант X значений, которые попали в i-ый интервал.