
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический метод решения задач линейного программирования.Содержание книги
Поиск на нашем сайте
Графический метод применяется для решения задач линейного программирования, когда число переменных равно 2 и задача линейного программирования записана в нормальной форме. В этом случае задача линейного программирования имеет вид:
При ограничениях
Решение каждого из неравенств представляет собой полуплоскость, определяющую данное неравенство. Нам нужно провести прямую Крайние точки – вершины этой области. Область допустимых решений – данная область. Область допустимых решений может представлять собой: Пустое множество
О
Причем значения целевой функции возрастают в направлении возрастания градиента Построить многоугольник допустимых решений; Построить прямую построить из начала координат вектор N; передвигать прямую в направлении вектора N (или в направлении –N, если ищем min) до тех пор, пока область допустимых значений D не окажется по одну сторону от прямой, и будет иметь с прямой хотя бы одну общую точку (такая прямая – опорная прямая или гиперплоскость) координаты этой прямой удовлетворяющие опорной прямой и области допустимых решений и будут являться оптимальным решением данной задачи.
В зависимости от области допустимых решений и целевой функции возможны следующие случаи:
решений нет
5)
6)
25. Симплекс метод Когда число переменных больше двух, то графический метод не работает, и переходят к другим аналитическим методам решения. Одним из основных аналитических методов решения задач линейного программирования является симплекс метод. Свое название он получил от латинского слова “простой”. Теория и алгоритм симплекс метода строятся для канонической формы задач линейного программирования. Как вытекает из графического метода решения задачи линейного программирования, оптимальное решение находится среди крайних точек (вершин) многоугольника допустимых решений. В общем случае, когда число переменных больше двух ограничения задают некоторую многогранную область. Известно, что экстремум (решение задачи линейного программирования) линейная функция достигает среди крайних точек этого многогранника. Это решение можно найти путем перебора всех этих крайних точек. Однако из-за большого числа вычислений такой путь практически невозможен. В симплекс методе используется целенаправленный перебор, когда переход от одной вершины в соседнюю происходит в направлении скорейшего возрастания целевой функции, поэтому при решении задачи линейного программирования симплекс методом выделяются следующие три этапа: отыскание какой-либо крайней точки; проверка оптимальности; указание процедуры целенаправленного перехода к следующей крайней точке. В этом состоит эвалистическое обоснование симплекс метода. Рассмотрим основные понятия симплекс метода. Пусть задача линейного программирования задана в канонической форме: План задачи линейного программирования – вектор, Базисный план Невырожденный базисный план – базисный план, содержащий ровно m ненулевых компонентов.
Оптимальный план задачи линейного программирования – план, составляющий максимальное значение целевой функции.
25 Первый этап: построение первоначального базисного плана. Пусть задача линейного программирования задана в канонической форме, причем среди векторов
Другими словами матрица условий имеет вид:
Полагая, что в системе (4) 25
|
||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.77.231 (0.009 с.) |

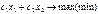 (1)
(1)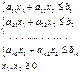 (2)
(2)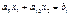 , после чего взять произвольную точку не лежащую на данной прямой. Обычно в качестве такой точки берут начало координат. Если координаты этой точки удовлетворяют заданному неравенству, то решением является полуплоскость от проведенной прямой, в которой лежит данная точка. Если же координаты не удовлетворяют неравенству, то решением является противоположная полуплоскость. А решением всей системы неравенств является выпуклая многоугольная область на плоскости.
, после чего взять произвольную точку не лежащую на данной прямой. Обычно в качестве такой точки берут начало координат. Если координаты этой точки удовлетворяют заданному неравенству, то решением является полуплоскость от проведенной прямой, в которой лежит данная точка. Если же координаты не удовлетворяют неравенству, то решением является противоположная полуплоскость. А решением всей системы неравенств является выпуклая многоугольная область на плоскости. Одна точка
Одна точка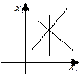 граниченный многоугольник
граниченный многоугольник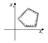 Неограниченная область
Неограниченная область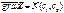 . Если мы будем двигаться в направлении вектора N, то значения целевой функции возрастают и наоборот. Таким образом, чтобы решить задачу линейного программирования нам надо найти такую точку области допустимых решений, через которую проходит прямая вида
. Если мы будем двигаться в направлении вектора N, то значения целевой функции возрастают и наоборот. Таким образом, чтобы решить задачу линейного программирования нам надо найти такую точку области допустимых решений, через которую проходит прямая вида  соответствующая наибольшему значению Z. Следовательно, для графического метода решения задачи линейного программирования нужно:
соответствующая наибольшему значению Z. Следовательно, для графического метода решения задачи линейного программирования нужно: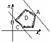 1)
1) 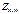 в т. A
в т. A на отрезке BC
на отрезке BC 2)
2)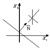 3)
3) в т. А
в т. А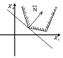 4)
4)
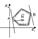
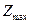 в т. В
в т. В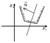
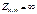
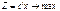 (1) при ограничениях Ax=b (2),
(1) при ограничениях Ax=b (2),  . Здесь матрица
. Здесь матрица 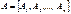 представляет собой набор векторов условий.
представляет собой набор векторов условий.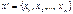 удовлетворяющий ограничениям (2).
удовлетворяющий ограничениям (2).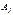 , соответствующие ненулевым компонентам, которого являются линейно независимыми.
, соответствующие ненулевым компонентам, которого являются линейно независимыми.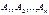 условий найдутся m линейно независимых единичных векторов, образующих единичный базис. Соответствующие им компоненты вектора x – базисные компоненты, а оставшиеся – свободные компоненты. И пусть вектор
условий найдутся m линейно независимых единичных векторов, образующих единичный базис. Соответствующие им компоненты вектора x – базисные компоненты, а оставшиеся – свободные компоненты. И пусть вектор 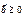 . Неограничивая общности, будем считать, что единичными базисными векторами будут первые m векторов. Тогда задача линейного программирования примет следующий вид:
. Неограничивая общности, будем считать, что единичными базисными векторами будут первые m векторов. Тогда задача линейного программирования примет следующий вид: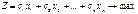 (3)
(3)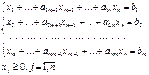 (4)
(4)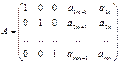
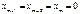 мы получим что
мы получим что 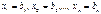 , и первоначальный базис угла будет
, и первоначальный базис угла будет 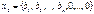 . Если же задача задана в нормальной форме, то всегда легко найти первоначальный базисный план.
. Если же задача задана в нормальной форме, то всегда легко найти первоначальный базисный план.


