
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения для совместных событий.Содержание книги
Поиск на нашем сайте
Вероятность суммы двух совместных событий равна сумме их вероятностей минус вероятность их совместного появления.
4. Формула полной вероятности. Следствием теоремы сложения и умножения вероятностей является формула полной вероятности. Теорема: Пусть событие A может произойти с одним из событий
Доказательство: События
Поскольку события
5. Схема Бернулли. Пусть производится серия из n испытаний, причем в каждом из испытаний событие A может появиться с постоянной вероятностью P и не появиться с вероятностью Теорема: формула Бернулли. Вероятность того, что в серии из n опытов событие A появится k раз, вычисляется по формуле Вывод формулы Бернулли. Вероятность одного сложного события состоит в том, что в серии n из испытаний событие A появится, раз и не появится n-k равно Пример: Пусть проводится серия из 4 испытаний. Причем будем рассматривать событие, когда A появляется три раза. Таких событий будет:
Формулой Бернулли удобно пользоваться в тех случаях, когда число испытаний небольшое. Если же число испытаний большое, то в этих случаях пользуются формулами Лапласа и Пуассона. 6. Локальная и интегральная теоремы Лапласа. Если вероятность P в схеме Бернулли не близка к 0 и единице, а число испытаний большое, то тогда вероятность того, что в серии из n испытаний событие появиться K раз вычисляется по формуле:
Для данной функции имеются специальные таблицы значений. Интегральная теорема Лапласа. Пусть в схеме Бернулли вероятность P отлична от 0 и не близка к 1, а число испытаний
Функция Ф(X) интегральная функция Лапласа. Для нее имеются специальные таблицы значений.
Формула Пуассона. В случае если в схеме Бернулли число испытаний большое, а вероятность стремиться к 0, то в этом случае пользуются формулой Пуассона:
где 7.
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.175 (0.005 с.) |


 Доказательство:
Доказательство: , образующих полную группу событий, называемых гипотезами. Тогда вероятность события A равна сумме произведений вероятности каждой гипотезы на условную вероятность события A при этой гипотезе.
, образующих полную группу событий, называемых гипотезами. Тогда вероятность события A равна сумме произведений вероятности каждой гипотезы на условную вероятность события A при этой гипотезе.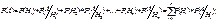
 .
. ;
; несовместны то и события
несовместны то и события  также будут несовместны и тогда, применяя теорему сложения, можно записать:
также будут несовместны и тогда, применяя теорему сложения, можно записать:
 . В этом случае говорят, что у нас действует схема Бернулли.
. В этом случае говорят, что у нас действует схема Бернулли.
 . Таких сложных несовместных событий будет столько, сколько можно сделать сочетаний из n элементов по k равно
. Таких сложных несовместных событий будет столько, сколько можно сделать сочетаний из n элементов по k равно  . Отсюда вытекает формула.
. Отсюда вытекает формула. .
.

 - дифференциальная функция Лапласа.
- дифференциальная функция Лапласа.
 , то тогда вероятность события
, то тогда вероятность события  состоящего в том, что событие A появится не менее,
состоящего в том, что событие A появится не менее,  раз и не более,
раз и не более,  раз вычисляется по формуле:
раз вычисляется по формуле: где
где

 .
.


