
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сумма событий. Теорема сложения вероятностей.Содержание книги
Поиск на нашем сайте
Сумма двух событий A и B – событие, состоящее в появлении события A или B одновременно. Оно обозначается Геометрическое растолкование суммы событий. Рассмотрим плоскость, на которую случайным образом точка, причем точка всегда попадает в плоскость. Тогда событие попадания точки в квадрат - достоверное. Площадь квадрата равна 1, тогда вероятность попадания точки в квадрат равна 1. А – вероятность попадания точки в область А.Вероятность равна В – вероятность попадания точки в область В. Вероятность равна Событие A+B означает, что точка попадет в эту область. Примеры:
А - попадание в цель при первом выстреле; В – попадание в цель при втором выстреле. A+B- вероятность попадания в цель: первый раз попал, второй промазал; первый раз промазал, второй попал; первый и второй попал. Основные свойства суммы событий.
4) если события 5) 3. Произведение событий. Теорема умножения вероятностей.
Произведение двух событий A и B – событие, состоящее в совместном появлении событий A и B. Замечание: когда речь идет о произведении событий, тогда используется союз и. Основные свойства произведения событий: 1) 2) 3) 4) если A и B несовместные события, то 5)
Теорема сложения вероятности несовместных событий. Вероятность суммы несовместных событий равна сумме их вероятностей.
Обычно для сокращения записи рассматривают два несовместных события.
Пусть пространство элементарных событий состоит из n элементарных исходов. Причем событию A благоприятствует Тогда сумме событий
Следствия: Если события Вероятность суммы противоположных событий равна 1.
Замечание: обычно вероятность события A обозначают p, тогда Теорема умножения. Событие A зависимое от события B, если его вероятность зависит от того, произошло ли событие B. Условная вероятность – вероятность появления события A при условии, что произошло событие B.
Основные свойства условной вероятности: Если событие A зависит (не зависит) от события B, то и событие B зависит (не зависит) от события A. Если события A и B независимы, то независимы Если события A и B независимы, то вероятность
Теорема: Вероятность произведения двух зависимых событий равна вероятности первого события умноженной на вероятность второго события, при условии, что первое произошло.
Доказательство: Доказательство приведем для двух событий, сводящихся к схеме случая. Пусть у нас имеется n элементарных исходов. Из них m - благоприятных событию A, L – событию B, k – их совместному появлению.
Замечание: теорема обобщается на случай произвольного числа событий.
Теорема: Вероятность произведения двух независимых событий равна произведению их вероятностей.
Независимые в совокупности события – несколько событий, вероятность которых не зависит от того какова совокупность других событий. Следствие: вероятность произведения независимых в совокупности событий равна произведению их вероятностей. 1) 2) Если события
Совместные события – события, появление одного и которых не исключает появления другого.
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.125.137 (0.005 с.) |

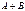 . Когда речь идет о сумме событий, то всегда ставится союз или.
. Когда речь идет о сумме событий, то всегда ставится союз или.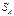 .
.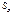 .
.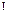 . Производится два выстрела про цели.
. Производится два выстрела про цели.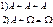
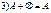
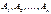 образуют полную группу, то
образуют полную группу, то 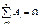
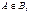 то A+B=B
то A+B=B
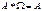
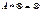
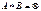

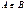 , то
, то 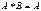
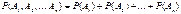

 Доказательство:
Доказательство: элементарных исходов, а событию B -
элементарных исходов, а событию B - 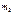 элементарных исходов. Поскольку события A и B – несовместные, то среди этих исходов нет общих.
элементарных исходов. Поскольку события A и B – несовместные, то среди этих исходов нет общих.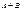 благоприятствует
благоприятствует 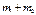 исходов.
исходов.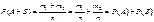
 образуют полную группу несовместных событий, то вероятность
образуют полную группу несовместных событий, то вероятность 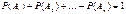 ;
;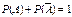
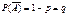

 и
и  ,
, 











