Основные уравнения движения подземных вод

Линейный закон фильтрации (закон Дарси) и пределы его применения

 

Движение подземных вод в пористых горных породах, как правило, характеризуется ламинарным режимом. Ламинарное движение подчиняется линейному закону фильтрации. Этот закон был установлен в 1856 г. Дарси на основании опытов по фильтрации в песке. Опыты производились в приборе, показанном на рис. 6.1.

 

 

Рис. 6.1. Прибор Дарси

 

В цилиндр загружался песок, который насыщался наливаемой сверху водой. Уровень воды поддерживался постоянным при помощи боковой отводной трубки. Вода просачивалась через песок и выливалась через кран внизу цилиндра. Для измерения потери напора при фильтрации вверху и внизу цилиндра вставлялись ртутные ма­нометры.

Опыты показали, что зависимость между расходом воды и потерей напора на единицу пути фильтрации выражается следующей формулой:

 

Q = k·(h/l)·w, (6.1)

 

где Q – количество воды, просачивающейся через песок в единицу времени; h – потеря напора; l – длина фильтрующей колонны песка; k – коэффициент фильтрации (постоянная величина, зависящая от физических свойств породы и фильтрующейся жидкости); w – площадь поперечного сечения фильтрующей колонны песка.

Разделим расход Q на площадь w и обозначим результат буквой v:

 

v =Q/w = k·(h/l), (6.2)

Величина v носит название скорости фильтрации. Она не представляет собой действительной скорости движения воды в порах, но есть некоторая приведенная величина, отнесенная ко всему сечению фильтрующей породы. С такой скоростью вода двигалась бы в том случае, если бы ею было занято все сечение пласта, как в трубах или каналах.

Величину действительной скорости движения воды в порах можно получить, разделив расход Q на площадь сечения пор, которая равна произведению общей площади w на коэффициент пористости р:

u =Q/w p, (6.3)

Сопоставляя выражения (6.2) и (6.3), получаем:

v = up (6.4)

Следовательно, скорость фильтрации равна произведению средней скорости движения воды в порах на коэффициент пористости. Так как р всегда меньше единицы, то скорость фильтрации всегда меньше средней скорости движения воды в порах.

Отношение (h/l) выражает собой величину падения напора на единицу длины пути фильтрации, т. е. величину напорного градиента, или пьезометрического уклона.

Обозначая (h/l) через I, имеем:

v = k·I. (6.5)

Эта формула показывает, что, по закону Дарси, при ламинарном движении скорость фильтрации пропорциональна напорному градиенту в первой степени.

Если принять I =1, то уравнение (6.5) примет вид:

v = k, (6.5а)

т. е. при напорном градиенте, равном единице, величина коэф­фициента фильтрации равна скорости фильтрации. Следовательно, коэффициент фильтрации должен выражаться в линейных единицах, отнесенных к единице времени: в м/сутки, м/сек или см сек.

По данным Г. Н. Каменского, линейный закон фильтрации применим с достаточной для практики точностью не только для мелкозернистых песков, но и для крупных песков и песчано-галечных образований при действительных скоростях движения подземных вод до 1000 м/сутки. Большей скоростью подземные воды обладают лишь в карстах и крупных трещинах. Следовательно, для решения гидрогеологических задач в большинстве случаев можно пользоваться линейным законом фильтрации.

Скорость движения, при которой происходит отклонение от закономерностей, установленных Дарси, называется критической скоростью. Для определения критической скорости v _кр можно пользоваться формулой Н. Н. Павловского:

v _кр = (1/6,5) · (0,75 p + 0,23) · (µ /ρ) · (Re/d), (6.6)

 

где v_кp – критическая скорость в см/сек; р – пористость породы; µ – вязкость воды; ρ – плотность воды; d – действующий диаметр зерен в см; Re – постоянное число; по определениям Н. Н. Павловского, для песков значение Re колеблется от 50 до 60.

 

Закон турбулентного движения и формула Краснопольского

В крупнообломочных и трещиноватых породах сохраняется ламинарный режим движения воды, если движение происходит с малой скоростью. Но при значительных скоростях (которые вполне возможны в указанных породах при относительно небольших градиентах) этот режим нарушается и развивается турбулентное движение.

Закон турбулентного движения воды в проницаемых породах выражается формулой Краснопольского:

 

Q = k _к ·w · √I, (6.7)

где k _к – коэффициент фильтрации породы.

 

Разделив расход Q на площадь поперечного сечения w, получим:

v = · k _к √I, (6.8)

Из уравнения (6.8) видно, что при турбулентном движении скорость потока пропорциональна квадратному корню из его уклона.

 

Уравнение Смрекера и его приложение

 

При смешанном или переходном режиме от ламинарного к турбулентному можно пользоваться формулой Смрекера:

Q = k _с ·w · , (6.9)

 

где k _с – коэффициент фильтрации породы; т — величина, зависящая от характера потока и свойств грунта, изменяющаяся от 1 до 2.

Эмпирические формулы для определения коэффициента фильтрации по механическому составу пород

Механический состав пород изображается в виде так называемых логарифмических кривых состава. Для построения кривых по оси абсцисс откладываются логарифмы диаметров частиц, а по оси ординат – суммарное содержание частиц от самых мелких до данного диаметра (рис. 6.2).

Рис. 6.2. График механического состава

По логарифмической кривой можно определить действующий диаметр и коэффициент неоднородности породы. Под действующим диаметром частиц d_e понимается такой диаметр, меньше которого имеют частицы, составляющие в породе 10%. Коэффициентом неоднородности k_n называется отношение диаметров частиц, соответствующих на оси ординат 60%, к действующему диаметру, т. е.

 

k_n = d₆₀/d_e, (6.10)

 

Формула Хазена. Для пород с коэффициентом неоднородности менее 5,0 и действующим диаметром в пределах от 0,1 до 3,0 мм при определении коэффициента фильтрации можно применять эмпирическую формулу Хазена:

 

k = Cd_е² (0,7 + 0,03 t), (6.11)

 

диаметр в мм; t – температура фильтрующейся воды в °С [(0,7 + 0,03 t)

– температурная поправка]; С – эмпирический коэффициент, изменяющийся от 400 до 1200 в зависимости от гранулометрического состава песка (чем крупнее зерна песка, тем больше числовой коэффициент).

Практическая работа № 7

Определение коэффициента фильтрации в естественных условиях методом инфильтрации воды из шурфа

Для определения коэффициента фильтрации грунтов, не насыщенных водой, в случаях, когда зеркало грунтовых вод находится на глубине не менее 2–3 м, проводят опыты по инфильтрации воды из шурфа, так как величина инфильтрации находится в прямой зависимости от водопроницаемости грунта.

Методика производства опытов и расчетов чрезвычайно многообразна. Наиболее часто применяют способы А. К. Болдырева, Г. Н. Каменского, Е. А. Замарина, Н. Н. Биндемана и Н. С. Нестерова и др.

 

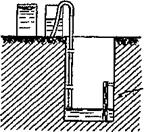
Способ А.К. Болдырева. В испытуемой породе вырывается шурф, не доходящий до уровня грунтовых вод на 1 м или более. На поверхности земли у бровки шурфа устанавливаются два сосуда определенной емкости (10–20 л), наполненные водой. Из этих сосудов по опущенной вниз трубке непрерывно подается вода на дно шурфа так, чтобы уровень воды в нем оставался все время постоянным – около 10 см над дном. Для наблюдения за уровнем воды на дне шурфа устанавливается рейка с делениями через 1 см (рис. 7.1).

 

Рис. 7.1. Схема установки для опытов по инфильтрации из шурфа по способу Болдырева

 

Определив количество воды Q, поступающей в шурф в единицу времени, и разделив его на площадь дна шурфа w, получим среднюю скорость инфильтрации:

 

v = Q/w, (7.1)

 

Коэффициент фильтрации определим по формуле (6.5):

 

k = v /·I.

 

А. К. Болдырев допускает, что при небольшой величине столба воды на дне шурфа, не более 10 см, создающийся при достаточно длительной инфильтрации напорный градиент равен единице и, следовательно,

k = v (7.2)

 

Таким образом, определяя непосредственно, опытным путем, скорость инфильтрации, тем самым получают величину коэффициента фильтрации.

Способ Болдырева дает преувеличенное значение коэффициента фильтрации, так как он не учитывает бокового растекания и капиллярных сил, производящих всасывание воды. Наиболее верные результаты он дает в песчаных грунтах, где влияние капиллярных сил не так велико.

Практическая работа № 8