
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы решения задачи КошиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
При использовании численных методов выполняется замена отрезка [ x0, X ] – области непрерывного изменения аргумента х множеством При этом xi называют узлами сетки. Во многих методах используются равномерные сетки с шагом
Задача Коши, определённая ранее на непрерывном отрезке [ x0, X ], заменяется её дискретным аналогом – системой уравнений, решая которую можно последовательно найти значения y1, y2, …, yn – приближённые значения функции в узлах сетки.
Численное решение задачи Коши широко применяется в различных областях науки и техники, и число разработанных для него методов достаточно велико. Эти методы могут быть разделены на следующие группы: · Одношаговые методы, в которых для нахождения следующей точки на кривой y = f(x) требуется информация лишь об одном предыдущем шаге. Одношаговыми являются метод Эйлера и методы Рунге – Кутта. · Методы прогноза и коррекции (многошаговые), в которых для отыскания следующей точки кривой y = f(x) требуется информация более чем об одной из предыдущих точек. Чтобы получить достаточно точное численное значение, часто прибегают к итерации. К числу таких методов относятся методы Милна, Адамса – Башфорта и Хемминга. · Явные методы, в которых функция Ф в выражении (1) не зависит от yn+1. · Неявные методы, в которых функция Ф зависит от yn+1.
Метод Эйлера Иногда этот метод называют методом Рунге-Кутта первого порядка точности. Данный метод одношаговый. Табулирование функции происходит поочередно в каждой точке. Для расчета значения функции в очередном узле необходимо использовать значение функции в одном предыдущем узле. Пусть дано дифференциальное уравнение первого порядка
с начальным условием y(x0) = y0. Выберем шаг h и введём обозначения: xi = x0 + i.h и yi = y(xi),,
где i = 0, 1, 2, … xi – узлы сетки, yi- значение интегральной функции в узлах. Иллюстрации к решению приведены на рисунке 2. Проведем прямую АВ через точку (xi,yi) под углом α. При этом tgα = f(xi,yi) (2) В соответствии с геометрическим смыслом задачи, прямая АВ является касательной к интегральной функции. Произведем замену точки интегральной функции точкой, лежащей на касательной AB. Тогда yi+1 = yi+Δy (3) Из прямоугольного треугольника АВС
Отсюда
Рисунок 2 - Метод Эйлера
Подставим в это выражение формулу (3), а затем преобразуем его. В результате получаем формулу расчета очередной точки интегральной функции:
Блок-схема процедуры решения дифференциального уравнения методом Эйлера приведена на рисунке 3.
Метод Эйлера – один из простейших методов численного решения обыкновенных дифференциальных уравнений. Но существенным его недостатком является большая погрешность вычислений. На рисунке 2 погрешность вычислений для i-го шага обозначена ε. С каждым шагом погрешность вычислений увеличивается.
|
|||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.60.144 (0.01 с.) |

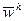 , состоящего из конечного числа точек x0 < x1 < … < xn = X – сеткой.
, состоящего из конечного числа точек x0 < x1 < … < xn = X – сеткой.
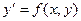
 (1)
(1) (4) Приравняем правые части (2) и (4). Получим
(4) Приравняем правые части (2) и (4). Получим  .
.

 (5) Из формулы (5) видно, что для расчета каждой следующей точки интегральной функции необходимо знать значение только одной предыдущей точки. Таким образом, зная начальные условия, можно построить интегральную кривую на заданном промежутке.
(5) Из формулы (5) видно, что для расчета каждой следующей точки интегральной функции необходимо знать значение только одной предыдущей точки. Таким образом, зная начальные условия, можно построить интегральную кривую на заданном промежутке.
 Рисунок 3 - Блок-схема процедуры решения дифференциального уравнения методом Эйлера
Рисунок 3 - Блок-схема процедуры решения дифференциального уравнения методом Эйлера


