
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка точности геодезических засечекСодержание книги
Поиск на нашем сайте Для определения координат пунктов маркшейдерских съемочных сетей широкое применение нашли геодезические засечки – прямые и обратные угловые, линейные и линейно-угловые. На точность определения положения определяемого пункта P влияет вид засечки, количество исходных пунктов и геометрия треугольников, образующихся между определяемым и исходными пунктами. Средняя квадратическая ошибка положения пункта P определяется по формуле
где h1 и h2 – диагональные элементы обратной весовой матрицы координат определяемого пункта Матрица N выглядит следующим образом
поэтому
где Таким образом, подставляя в формулу (4.29) элементы матрицы N, получаем формулу определения средней квадратической ошибки положения пункта P в общем виде
где m – ошибка единицы веса. При оценке точности пунктов маркшейдерских съемочных сетей за ошибку единицы веса в формуле (4.31) принимается средняя квадратическая ошибка измерения горизонтальных углов m b = 20². В линейной засечке m = ml и значения mP принимаются в метрах, поэтому необходимо произвести переход от угловых величин к линейным, воспользовавшись отношением (4.13)
где ml – средняя квадратическая ошибка линейных измерений, мм. Подкоренное выражение формулы (4.31) зависит от вида и геометрии засечек. Для вывода формул ошибки положения пункта P по каждой засечке приведем исходные данные к общему виду. При 3-х исходных пунктах засечки можно представить в виде двух треугольников (рис. 4.40). Так как ошибка положения пункта не зависит от направления осей прямоугольной системы координат, направим ось х по линии 2-Р так, как это показано на рис. 4.47. Используем теорию параметрического уравнивания. Обозначим координаты пункта Р через параметры:
ХР = Т 1 ; YP = Т 2.
Рассмотрим сначала однократные засечки.
Рис. 4.47. Общая схема засечек
Прямая угловая засечка При прямой угловой засечке измеряются углы β1 и β2 . Выразим эти углы через координаты исходных пунктов и параметры:
(4.33)
Дифференцируя выражения (4.33) по параметрам, найдем элементы матрицы А:
Введем обозначения:
Так как углы измерены равноточно, матрица весов Р – единичная, и элементы матрицы N вычислены по формулам:
По формуле (4.31) получим ошибку положения пункта
Линейная засечка При линейной засечке измеряются стороны l 1 и l 2 . Выразим их через координаты исходных пунктов и параметры:
(4.35)
Дифференцируя выражения (4.35) по параметрам, найдем элементы матрицы А:
Матрица весов Р – не единичная, т. к. линейные измерения – неравноточные. Примем за ошибку единицы веса
Элементы матрицы N вычисляем по формулам:
По формуле (4.31) получим ошибку положения пункта
Если ошибки линейных измерений имеют вид
то ошибка положения пункта Р
Прямая линейно-угловая засечка. Прямая линейно-угловая засечка заключается в измерении углов β1, β2 и сторон l 1, l 2. Используя решения угловой и линейной засечек, запишем матрицы А и Р:
После преобразований получим
Обратная угловая засечка. При обратной угловой засечке измеряются углы γ1 и γ2 . Для обратных засечек при выводе формул удобно центр системы координат поместить в пункт Р, а ось х направить вдоль стороны Р 2 (см. ось х1 на рис. 4.46). Выразим углы γ1 и γ2 через координаты исходных пунктов и параметры:
(4.39)
Дифференцируя выражения (4.39) по параметрам, найдем элементы матрицы А:
Матрица весов Р – единичная, ошибка единицы веса
или
или
Ошибка положения определяемого пункта при однократной обратной угловой засечке (в случае измерения углов γ1 и γ2)
Обычно при точке Р измеряются не углы γ1 и γ2, а направления NP 1, NP 2 и NP 3 и μ = mN =
где Тр – третий параметр (ориентирный угол) [26]. Дифференцируя выражения (4.43) по параметрам, найдем элементы матрицы А:
Последняя строка матрицы А (элементы а 41 и а 42) вводится в связи с переходом к эквивалентной системе уравнений поправок для исключения третьего параметра Тр [26]. Матрица весов теперь не будет единичной, т. к. р 4 = р S = – 1 / 3:
Далее получим:
или
или
Ошибка положения определяемого пункта при однократной обратной угловой засечке (в случае измерения направлений NP 1, NP 2 и NP 3)
Формулы оценки точности обратной угловой засечки содержат некий графический смысл. Если отложить на направлениях Р -1, Р -2, Р -3 (см. рис. 4.48) градиенты r 1, r 2, r 3, получим так называемый обращенный треугольник АВС [30] со сторонами с 12, с 13, с 23. Используя тригонометрические соотношения, в формулах (4.40), (4.41), (4.44), (4.45) можно записать:
где S – площадь обращенного треугольника.
Рис. 4.48. Построение обращенного треугольника
Формулы для определения ошибки положения определяемого пункта через элементы обращенного треугольника имеют вид: для засечек с измеренными углами
для засечек с измеренными направлениями
Несмотря на простой вид формул (4.47) и (4.48) для расчетов они неудобны, и лучше пользоваться формулами (4.42) и (4.46).
|
||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

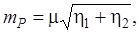 (4.29)
(4.29)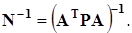
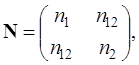 (4.30)
(4.30)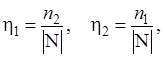
 – определитель матрицы N.
– определитель матрицы N.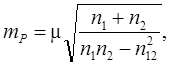 (4.31)
(4.31)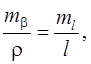 (4.32)
(4.32)
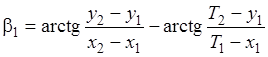 ;
;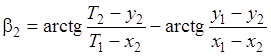 .
.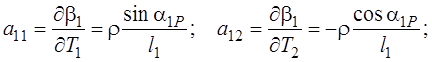
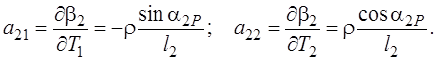
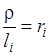 – градиенты направлений [30]. Учтем, что:
– градиенты направлений [30]. Учтем, что: 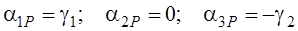 . Тогда для матрицы А получим:
. Тогда для матрицы А получим: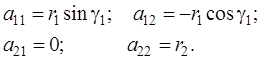
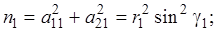
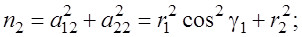
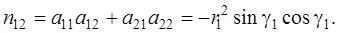
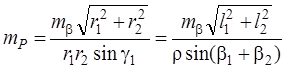 .
.  (4.34)
(4.34)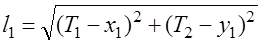 ;
;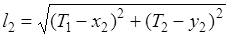 .
.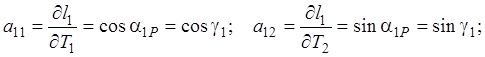
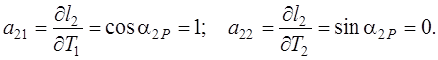
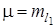 . Матрица весов измеренных длин
. Матрица весов измеренных длин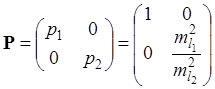 .
.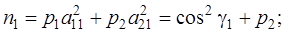
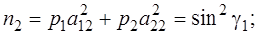
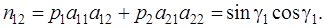
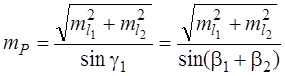 .
. 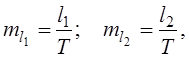 (4.37)
(4.37)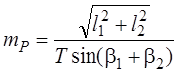 . (4.38)
. (4.38)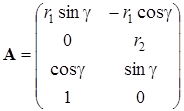 ;
; 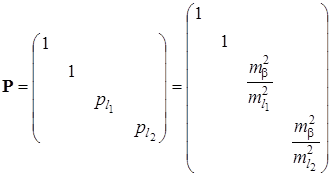 .
.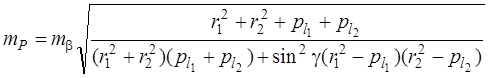 .
.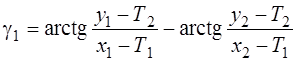 ;
;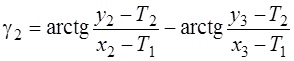 .
.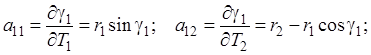
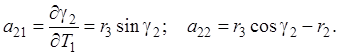
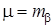 . Далее получим:
. Далее получим: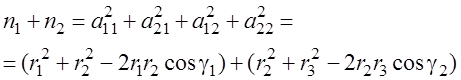 , (4.40)
, (4.40)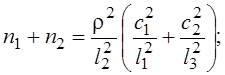
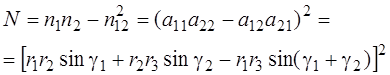 , (4.41)
, (4.41)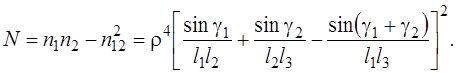
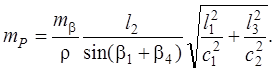 (4.42)
(4.42)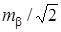 [29]. Уравнения связи для измеренных направлений будут иметь вид:
[29]. Уравнения связи для измеренных направлений будут иметь вид: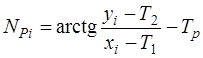 , (4.43)
, (4.43)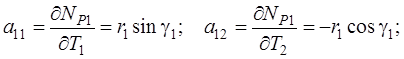
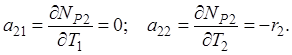
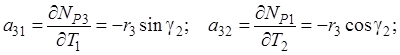
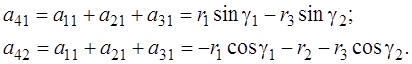
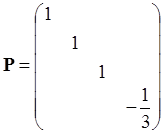 .
.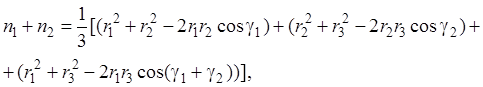 (4.44)
(4.44)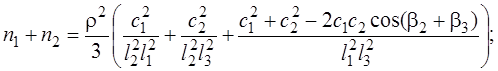
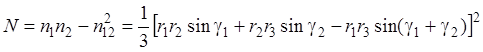 , (4.45)
, (4.45)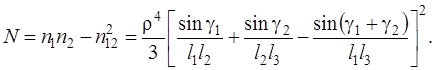
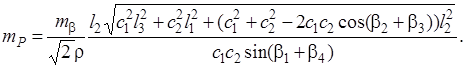 (4.46)
(4.46)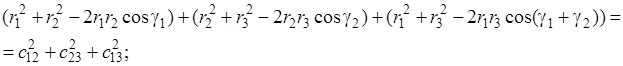
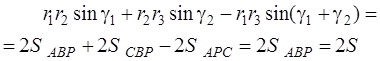 ,
,
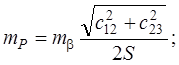
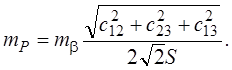 (4.48)
(4.48)


