
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проектирование и уравнивание маркшейдерских сетейСодержание книги
Поиск на нашем сайте
Построение маркшейдерских опорных и съемочных сетей выполняется по техническому проекту, разработанному на основе технического задания. Техническое задание составляется главным маркшейдером предприятия и утверждается главным инженером. В техническом задании указывается: ·цель проектируемых работ – создание или реконструкция сети (в т.ч. развитие существующей сети); ·тип проектируемой сети – маркшейдерская опорная сеть или маркшейдерская съемочная сеть; ·назначение сети; ·класс точности проектируемой сети или предельные ошибки положения новых пунктов сети относительно исходных; ·характеристика исходных пунктов государственной геодезической сети или маркшейдерской опорной сети на территории предприятия – их местоположение, каталог координат, класс точности, наружное оформление знаками. При выполнении работ силами сторонних организаций согласовываются сроки и стоимость работ по проектированию и созданию сети. Технический проект построения сети разрабатывается исполнителем работ. Технический проект может содержать текстовую, графическую и сметную части [33]. В текстовой части проекта отражаются следующие вопросы: · тип и назначение проектируемой сети; · краткая физико-географическая характеристика района работ; · сведения о геодезической обеспеченности района работ; · определение метода построения сети и выбор необходимых приборов; · предварительный расчет ожидаемой точности плановых координат и высот пунктов сети; · организация и сроки выполнения полевых работ, мероприятия по технике безопасности и охране труда; · перечень материалов, подлежащих сдаче по окончании работ. Графическая часть проекта составляется на плане масштаба принятого на горном предприятии. На план наносятся: исходные пункты и стороны, определяемые пункты и схема построения сети. В сметной части проекта производится расчет необходимых затрат на выполнение проектируемых работ в соответствии с действующими нормами выработки (времени). Выбор метода построения сети зависит: от имеющихся в распоряжении исполнителя работ приборов; от формы и размеров участка проектирования; рельефа местности и застроенности территории, условий видимости; наличия и расположения исходных пунктов.
Различают необходимые и избыточные исходные данные. Например, для центрирования, ориентирования и масштабирования сети триангуляции необходимо располагать четырьмя (КМ = 4) исходными данными – плановыми координатами двух пунктов сети или координатами одного пункта, дирекционным углом и длиной одной стороны сети. В трилатерации и полигонометрии КМ = 3 (координаты пункта и дирекционный угол стороны сети), в высотных сетях КМ = 1 (высотная отметка одного из реперов сети). Все остальные исходные данные будут избыточными. Если число исходных данных в сети равняется необходимому числу исходных данных, т. е. L = КМ, сеть называется нуль-свободной. При L < КМ сеть называется свободной, при L > КМ – несвободной сетью. При проектировании сети следует иметь в виду, что включаемые в сеть исходные пункты должны быть взаимно увязаны – координаты их должны быть вычислены в одной системе и не вызывать сомнений у работников маркшейдерской службы по результатам выполненных ранее работ. Класс точности исходных пунктов должен быть выше точности развиваемой сети. В этом случае координаты исходных пунктов можно принять безошибочными (истинными) и ошибки исходных данных не учитывать при предварительной оценке точности и при уравнивании результатов полевых работ. К измеряемым величинам в маркшейдерско-геодезической практике относятся направления, углы, азимуты, длины сторон, приращения координат (при спутниковых наблюдениях) и т.д. В плановой сети для определения координат новых пунктов от исходных достаточно выполнить два измерения – двух сторон, двух углов или угла и стороны сети. В высотной сети достаточно одного измерения – превышения. Поэтому число необходимых измерений в плановых сетях К = 2 р, в высотных сетях К = р, где р – число определяемых пунктов. При спутниковом позиционировании К = 3 р, т. к. определяются координаты (приращения координат) по всем трем осям. Если измерено N величин Х 1, …, ХN, то число избыточно измеренных величин R = N – K.
Каждое избыточное измерение влечет появление математических отношений между измеренными или измеренными и исходными величинами. Избыточные исходные данные математических условий не образуют.
Геодезические и маркшейдерские сети обязательно должны содержать избыточные измерения. Они нужны для своевременного обнаружения грубых ошибок, а также для производства уравнительных вычислений и оценки качества выполненных работ. Кроме того, точность элементов сети после уравнивания повышается в среднем в Избыточность измерений достигается: в триангуляции, трилатерации и спутниковых наблюдениях – построением замкнутых геометрических фигур – треугольников и цепочек треугольников, многоугольников с диагоналями, центральных фигур и т. д., в вершинах которых должно быть не менее двух исходных пунктов; в полигонометрии и высотных ходах – проложением замкнутых ходов, ходов между двумя исходными пунктами, ходов с узловыми точками и проч. Схема проектируемой сети переносится на план местности для определения объемов работ и проверки выполнения требований инструкций к элементам сети – углам фигур, длинам сторон и ходов. Выполняется предварительный расчет ожидаемой точности плановых координат и высот пунктов сети. Для простых фигур и несложных сетей – засечек, вытянутых полигонов и разомкнутых высотных ходов – можно применить формулы, рассмотренные в главе. Сложные построения анализируются при помощи специальных компьютерных программ. При анализе проекта можно решать задачи двух основных типов: прямая задача – по заданной точности измерений и геометрии сети находят ожидаемую точность элементов сети – ошибки положения новых пунктов относительно исходных; ошибки взаимного положения новых пунктов; линейные и угловые ошибки наиболее слабых сторон сети; обратная задача – по нормативным значениям ошибок элементов сети и ее геометрии определяют необходимую точность измерений. Для решения этих задач применяются формулы из теории параметрического уравнивания. В случае проектирования плановых сетей обозначим координаты новых (определяемых) пунктов:
Для каждого из N запроектированных измерений составляется параметрическое уравнение связи Xi = j i (T 11, …, Tp 2). Затем формируется матрица коэффициентов системы нормальных уравнений поправок А =
где
где μ – априорное значение ошибки единицы веса (принимается μ = m β при полигонометрии и триангуляции и μ = ml при трилатерации и спутниковых наблюдениях). Априорная точность измерений устанавливается в проекте в соответствии с применяемыми приборами и методиками измерений. Обратный вес функции, описывающей оцениваемый элемент сети, определяется по формуле
где: матрица N = A T PA; P – матрица весов измеряемых величин; s – вектор-строка производных функции F по параметрам T 11, …, Tp 2. Если определяется ошибка положения i -го пункта сети (xi = Ti 1, yi = Ti 2), то
qF = h i 1 + h i 2, (4.58)
где h i 1 и h i 2 – диагональные элементы обратной весовой матрицы координат определяемого пункта Если определяется ошибка стороны lij, то
s =
Если определяется ошибка взаимного положения i -го пункта сети (xi = Ti 1, yi = Ti 2) и j -го пункта сети (xj = Tj 1, yj = Tj 2), то
qF = w1 + w2, (4.59)
где w1 и w2 – диагональные элементы матрицы
W = SN-1S T,
S = Полученные значения ошибок сравниваются с нормативными значениями, приведенными в инструкциях по производству маркшейдерских и геодезических работ. При этом от предельных ошибок, указанных в инструкции, необходимо перейти к средним квадратическим ошибкам, разделив их на 3 (двумерный случай – ошибки положения на плоскости) или на 2,5 (одномерный случай). Если проект не обеспечивает необходимую точность элементов сети, следует повысить точность измерений или изменить геометрию сети. В случае проектирования высотных сетей обозначим координаты новых (определяемых) пунктов:
Для каждого из N запроектированных ходов между реперами составляется параметрическое уравнение связи Xi = j i (T 1, …, Tp). Матрица коэффициентов системы нормальных уравнений поправок
А =
где Априорное значение ошибки единицы веса принимается μ = m 1 км , а элементы весовой матрицы pi = 1/ L км , где L км – длины ходов, км. Если определяется ошибка положения i -го пункта сети (zi = Ti), то
qF = h i, (4.60)
где h i – диагональный элемент обратной весовой матрицы Если определяется ошибка превышения между пунктами – взаимного положения i -го пункта сети (xi = Ti) и j -го пункта сети (xj = Tj), то
s = При решении обратной задачи находят ошибку единицы веса
где DF – допуск, установленный инструкцией для точностной характеристики элемента сети; kз – коэффициент перехода от допуска к средней квадратической ошибке (3 или 2,5). Точность любого проектируемого измерения в сети находят по формуле
По найденным значениям точности отдельных измерений подбираются приборы для выполнения работ по созданию сети. После выполнения полевых работ и первичной обработки результатов измерений выполняется уравнивание сети. В зависимости от вида сети и числа избыточных измерений применяется коррелатный или параметрический способы уравнивания. Коррелатный способ уравнивания применяется при уравнивании полигонов, когда число избыточных измерений R много меньше числа достаточных измерений K. Сложные построения уравниваются параметрическим способом. Современный уровень вычислительной техники позволяет отказаться от приближенных способов уравнивания, который не обеспечивает строгий анализ точности сети. Анализ точности по результатам параметрического уравнивания выполняется по формулам (57) – (60), но ошибка единицы веса рассчитывается по формуле
где μ1 – апостериорная ошибка единицы веса, vi – поправки в результаты измерений. Качество работ оценивается близостью априорной и апостериорной ошибок единиц веса, чем меньше отличие, тем лучше качество. Результаты оценки точности выполненных работ по материалам уравнивания приводятся в отчете, передаваемом исполнителем работ предприятию, и являются основанием для приемки выполненных работ.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.103.151 (0.012 с.) |

 раз [4].
раз [4].
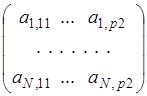 ,
, , I = 1 … N, k = 1 … 2 p. Для вычисления значений элементов матрицы А используются приближенные значения координат новых пунктов, дирекционных углов и длин сторон проектируемой сети, снимаемые с плана. Оценка точности элементов сети производится по формуле
, I = 1 … N, k = 1 … 2 p. Для вычисления значений элементов матрицы А используются приближенные значения координат новых пунктов, дирекционных углов и длин сторон проектируемой сети, снимаемые с плана. Оценка точности элементов сети производится по формуле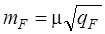 , (4.57)
, (4.57) qF = sN-1s T,
qF = sN-1s T,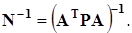
 .
. .
.
 ,
, .
. , (4.61)
, (4.61) . (4.62)
. (4.62) ,
,


