
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрического нивелированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Важной характеристикой точности работ по геометрическому нивелированию является средняя квадратическая ошибка двойного нивелирования 1 км хода Для расчета СКО на 1 км двойного хода применяется формула
Для высотных маркшейдерских опорных и съемочных сетей получим: III класс – IV класс – техническое нивелирование – Эти значения хорошо согласуются с нормативными характеристиками (см. табл. 4.7). В табл. 4.9 приведены современные нивелиры, точность которых отвечает требованиям, предъявляемым к маркшейдерским высотным сетям. Формула (4.21) получена для свободных ходов. Ошибка положения любой k -ой точки хода определяется по этой же формуле, но с заменой n = k. С увеличением номера точки возрастает ошибка положения точки.
Таблица 4.9 Современные нивелиры, точность которых отвечает требованиям, предъявляемым к маркшейдерским высотным сетям
На практике часто ходы прокладываются между реперами более высокого разряда. Если полученная при этом невязка не превысила допустимые значения, то выполняется уравнивание хода – невязка распределяется с обратным знаком поровну на все превышения. Погрешностями исходных реперов пренебрегают. Рассмотрим нивелирный ход, проложенный между двумя реперами А и В (рис. 4.45).
Рис. 4.45. Нивелирный ход между реперами А и В
Поправка в превышение вычисляется по формуле
где невязка После введения поправок в превышения, высотная отметка k-ой точки хода равна
С учетом принятых допущений (
Заметим, что первые k производных равны
Функция (4.25) достигает максимум при k = 0,5 n, т. е. наибольшую ошибку имеет пункт, находящийся в середине хода. Причем эта ошибка в 2 раза меньше ошибки последнего пункта свободного хода (при той же длине хода). На рис. 4.46 представлено распределение ошибок положения пунктов в высотных ходах – свободном и несвободном. Расчеты выполнены по формулам (4.21) и (4.25) для n = 10, средние квадратические ошибки пунктов выражены в средних квадратических ошибках превышений mh, т. е по оси ординат даны значения подкоренных выражений в расчетных формулах.
Рис. 4.46. Распределение ошибок положения пунктов в высотных ходах
Появление светодальномеров, а в последние годы электронных тахеометров способствовало широкому внедрению в практику построения планово-высотных сетей метода тригонометрического нивелирования. Превышение между двумя пунктами при тригонометрическом нивелировании
где l – измеренная наклонная длина линии; δ – вертикальный угол (или зенитное расстояние); i и v – высоты инструмента и визирной цели. Дифференцируем формулу (4.26) и найдем дисперсию превышения по правилам теории ошибок
Для хода, состоящего из n вершин, погрешность высотной отметки последнего пункта определится из формулы
Примем закон ошибок линейных измерений в форме
Приравняем в соответствии с принципом равных ошибок
или
Опыт тригонометрического нивелирования с помощью электронных тахеометров показывает, что оптимальными можно считать длины сторон тригонометрического хода 300-400 м. При больших сторонах начинает сказываться ошибка наведения, и точность измерения вертикального угла снижается. Меньшие стороны приводят к росту числа стоянок. Сравнивая формулы (4.22) и (4.28), найдем при l = 0,4 км и Т = 100 000 (4-й класс полигонометрии) предельное значение для μ (kз = 2): μпред
что соответствует точности геометрического нивелирования III класса. Аналогично получится, что если приборы и методика обеспечивают точность полигонометрии 1-го разряда, то тригонометрическое нивелирование обеспечит точность геометрического нивелирования IV класса. Второму разряду полигонометрии будет соответствовать тригонометрическое нивелирование технической точности.
В табл. 7 приведены сведения о современных электронных тахеометрах, применяемых при создании маркшейдерских опорных сетей.
Таблица 4.10
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 1100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.127.77 (0.011 с.) |


 или средняя квадратическая ошибка среднего из прямого и обратного ходов длиной 1 км. Именно эта характеристика является паспортной точностью нивелиров и служит для выбора нивелира при проектировании работ.
или средняя квадратическая ошибка среднего из прямого и обратного ходов длиной 1 км. Именно эта характеристика является паспортной точностью нивелиров и служит для выбора нивелира при проектировании работ.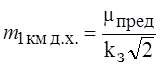 . (4.24)
. (4.24) = 3,5 мм (μ = 10 мм, kз = 2);
= 3,5 мм (μ = 10 мм, kз = 2); = 7 мм (μ = 20 мм, kз = 2);
= 7 мм (μ = 20 мм, kз = 2);

 ,
, .
.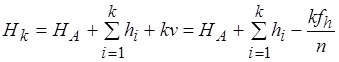 .
. ) найдем среднюю квадратическую ошибку высотной отметки k-ой точки хода
) найдем среднюю квадратическую ошибку высотной отметки k-ой точки хода .
. , а следующие (n – k) производных равны
, а следующие (n – k) производных равны  . Поэтому получим
. Поэтому получим

 , (4.26)
, (4.26)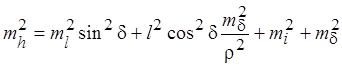 .
. .
.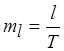 и пусть mi = mv. Тогда
и пусть mi = mv. Тогда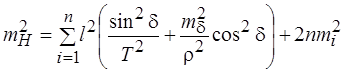 . (4.27)
. (4.27) и пренебрежем вторым слагаемым. Для двойного равностороннего хода получим
и пренебрежем вторым слагаемым. Для двойного равностороннего хода получим ,
, . (4.28)
. (4.28) 9 мм,
9 мм,


