
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка точности двукратных засечекСодержание книги
Поиск на нашем сайте
В табл. 4.14 приведены значения коэффициента k, полученные при m b = 20² и различных значениях горизонтальных углов b.
Таблица 4.14 Значения коэффициента k для двукратных засечек
Из таблиц 4.13 и 4.14 можно заключить: при равных условиях наиболее высокую точность обеспечивает обратная угловая засечка, уравненная по направлениям, а при γ < 55º – прямая угловая засечка; ошибка положения пункта принимает наименьшее значение при следующих значениях угла γ – 122º и 128º (соответственно, прямая угловая и линейная засечки); точность обратной угловой засечки с измеренными направлениями выше точности засечки с измеренными углами (при γ < 110º); повышение точности двукратных засечек относительно точности однократных засечек происходит не просто в Точность засечек прямо пропорционально зависит от точности угловых (и линейных) измерений m b и от длины базисной стороны c. Это позволяет с помощью таблиц 4.12 и 4.14 выполнять оценку точности засечек при других условиях измерений. При этом значения коэффициента k будут пропорционально изменяться в зависимости от точности угловых измерений m b. Пример. Оценить ошибку положения пункта P, определяемого с помощью обратной угловой засечки по измеренным направлениям с 4-х исходных пунктов (двукратная засечка). Значения базисов c 1 = 0,2 км, c 2 = 0,4 км, c 3 = 0,6 км. Среднее значение горизонтального угла при исходных пунктах Значение коэффициента k = 0,046 (при m b = 20²) определяется из таблицы 4.14 (для двукратных засечек) при b = 40°. Для заданных условий коэффициент k определяется из выражения
Тогда
Ответы, получаемые по формулам (табл. 4.11 и табл. 4.13), имеют некоторую погрешность, обусловленную тем, что вместо точных значений геометрических элементов принимались средние их значения, и расчет формул выполнялся по упрощенному принципу (b = b1 = b2 = b3 = b4, l = l 1 = l 2 = l 3).
Точность спутниковых геодезических Технологий Наряду с традиционными методами создания маркшейдерских опорных и съемочных сетей в последние десятилетия все более широкое применение на карьерах находят спутниковые геодезические технологии. В геодезическом смысле они реализуют принцип пространственной обратной линейной засечки – когда пространственные координаты (x, y, z) пункта наземной сети определяются по расстояниям, измеренным от этого пункта до четырех и более спутников, положение которых известно с достаточной точностью. Основным достоинством спутниковых систем является их оперативность, всепогодность, оптимальная точность и эффективность. Для измерений не нужна видимость между определяемыми пунктами. Метод определения координат геодезических пунктов с помощью спутниковых систем называют позиционированием. Анализ точности позиционирования начнем с простой схемы (рис. 4.49). Пусть определяются координаты XP, YP, ZP по измеренным расстояниям (дальностям) от определяемого пункта P до трех спутников – 1, 2 и 3. Рассмотрим пирамиду 123Р, для которой примем два условия: основание пирамиды равносторонний треугольник 123, расположенный в горизонтальной плоскости, а ребра – l 1, l 2 , l 3 – равны между собой и наклонены к горизонту (как и к основанию пирамиды) под углом δ. Центр системы координат поместим в точку Р, ось z направим по высоте пирамиды вверх к основанию, а ось х – через точку 1. В равностороннем треугольнике 123 точка О – место пересечения медиан – отстоит от вершин треугольника на расстояние R (радиус описанной окружности), а от сторон треугольника на расстояние R/2. Учитывая, что в равностороннем треугольнике медиана – и биссектриса, и высота треугольника – она делит внутренние углы треугольника (60º) пополам.
Рис. 4.49. Позиционирование от трех спутников
Запишем в принятой системе координаты вершин пирамиды:
Обозначим координаты определяемого пункта Р через параметры:
ХР = Т 1 ; YP = Т 2; ZP = T 3.
Выразим измеренные величины через координаты исходных пунктов и параметры:
Дифференцируя выражения (4.55) по параметрам, найдем элементы матрицы А:
Примем линейные измерения равноточными и матрицу весов Р – единичной, примем за ошибку единицы веса
Диагональные элементы матрицы Q P используются для расчета ошибки положения пункта P:
в плане в пространстве по высоте
Элементы матрицы Q P определяются только геометрией засечки. В теории анализа точности спутниковых геодезических измерений используется понятие геометрического фактора (ГФ) – отношение ошибки положения пункта к ошибке единицы веса [31] ГФ В зависимости от вида ошибки положения (в плане, по высоте или в пространстве) геометрический фактор имеет следующие обозначения:
Из формулы (56) следует связь
PDOP 2 = HDOP 2 + VDOP 2. Для нашего примера: q 11 = q 22 =
Таблица 4.15 Влияние угла возвышения δ на точность позиционирования
Из таблицы следует, что хорошие результаты получаются при небольших углах возвышения спутников – 30º… 40º. Вообще геометрический фактор зависит также от широты местности, количества наблюдаемых спутников и других факторов. ГФ становится меньше при наблюдении более 4 спутников, достаточно хорошим считается наблюдение шести спутников. Основным показателем ГФ является PDOP. Для оценки качества засечки пользуются следующей шкалой:
Геометрический фактор – не единственный источник ошибок при спутниковых геодезических измерениях. Источниками формирования ошибки определения расстояния от приемника до спутника являются также [32, 33]: оборудование космического аппарата и наземный контрольно-измерительный комплекс; среда распространения сигнала от спутника к приемнику станции наблюдения; приемная станция; методика наблюдений и обработки результатов измерений. Ошибки от первого источника обусловлены неидеальностью частотно-временного и эфемероидного обеспечения спутников. Погрешности частотно-временного обеспечения возникают при сверке и хранении бортовой шкалы времени. Наблюдение и корректировку часов на спутнике ведут наземные контрольно-измерительные комплексы. Эфемериды (координаты) спутника в момент отправки сигнала содержат ошибки вследствие влияния внешних факторов – Солнца, Земли, Луны и проч. Корректировка координат спутника производится также контрольно-измерительными комплексами. Перечисленные ошибки практически исключаются при дифференциальных наблюдениях. При распространении радиосигнала от спутника к приемной станции скорость его не остается постоянной, а меняется на различных участках атмосферы – особенно в ионосфере и тропосфере. Снижение влияния ионосферы на результаты позиционирования происходит за счет использования двух несущих частот и работы на двухчастотных приемных станциях. Задержка радиосигналов в тропосфере наиболее сказывается при наблюдениях за спутниками, имеющими угол возвышения над горизонтом δ < 10º – 15º. Поэтому спутники с малым углом возвышения не отслеживаются. Эта мера направлена и на снижение влияния ошибок за счет изменения пути радиосигнала вследствие отражения от поверхности земли, зданий и других объектов, находящихся поблизости от приемной станции. Для снижения влияния многолучевости (многопутности) радиосигнала рекомендуется: выбирать место наблюдений вдали от отражающих объектов; устанавливать дополнительные экранирующие приспособления; увеличивать время работы на станции. Инструментальные ошибки или ошибки работы на приемной станции в большинстве своем исключаются при дифференциальных наблюдениях. К таким ошибкам относятся погрешности хода часов в приемнике, временные задержки в многоканальных приемниках. Неустраняемыми являются ошибки измерения высоты и центрирования прибора и антенны. Их значения составляют первые миллиметры и входят в составляющую a средней квадратической ошибки GPS-измерений. Общая ошибка спутникового позиционирования описывается линейной функцией
где для высокоточных моделей приемников и методов измерений а составляет 2…5 мм, а b – 1 … 3 мм/км. При этом точность координаты z в 2 – 3 раза ниже точности определения плановых координат. Тип приемника, методика наблюдений и последующей обработки результатов измерений (постобработка) являются определяющими при оценке точности позиционирования. Современные кодово-фазовые многоканальные двухчастотные приемники позволяют работать как в кодовом, так и в более точном – фазовом режиме. Кодовым методом проводят абсолютные наблюдения – определяют непосредственно координаты пункта, на котором установлен приемник. Фазовый метод применяют при относительных (дифференциальных) измерениях, когда определяют приращения координат между пунктами-станциями, на которых одновременно работают GPS-приемники, причем одна из этих станций – базовая, с известными координатами. Из этих относительных измерений образуют разности трех типов: простые, сдвоенные и строенные. Разности практически свободны от большинства погрешностей. Так первые или простые разности (разности измерений между приемниками) не содержат искажений аппаратуры спутника, ослаблены влияния атмосферных воздействий и погрешности эфемерид. Чем ближе расположены станции A и B, тем полнее компенсированы искажения. Вторые разности (разности измерений между спутниками) свободны как от искажений на спутнике, так и от искажений на наземных станциях. Вторые и третьи разности используются в постобработке и уравнительных вычислениях для оценки фактической точности измерений.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.60 (0.007 с.) |




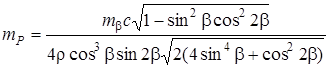

 раз, а зависит от геометрии засечки.
раз, а зависит от геометрии засечки. . СКО угловых измерений m b = 5².
. СКО угловых измерений m b = 5².


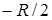



 (4.55)
(4.55)



 . Обратная весовая матрица координат определяемого пункта
. Обратная весовая матрица координат определяемого пункта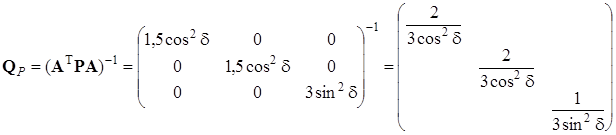 .
.


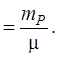


 (4.56)
(4.56) ; q 33 =
; q 33 = 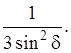 В табл. 4.15 приведены значения геометрического фактора при различных углах возвышения спутников над горизонтом.
В табл. 4.15 приведены значения геометрического фактора при различных углах возвышения спутников над горизонтом. ,
,


