
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжения в наклонной площадке. Главные напряжения при изгибе и их эпюры.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
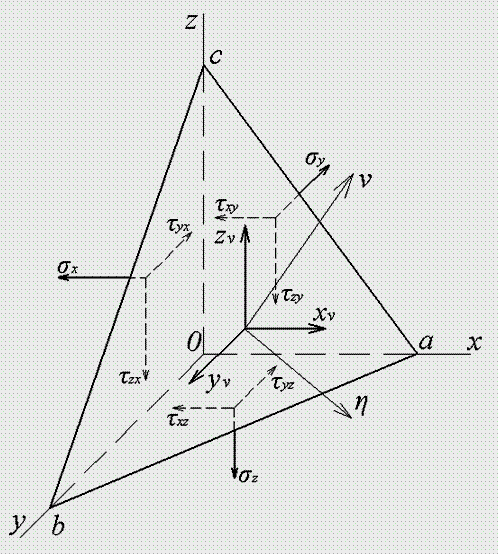
Для исследования напряженного состояния тела в любой его точке нужно уметь определять напряжения не только на площадках, параллельных координатным плоскостям, но и на наклонных. Положение бесконечно малой наклонной площадки
Рис.1.2. Напряжения на наклонной площадке Наклонная площадка и координатные плоскости образуют бесконечно малый тетраэдр Рассмотрим силы, действующие на тетраэдр. На координатных площадках это будут силы от шести составляющих напряжений Спроектируем действующие силы на ось х: Опуская слагаемое третьего порядка малости и разделив все на Аналогичным образом можно получить еще два уравнения, и тогда уравнения равновесия элементарного тетраэдра имеют вид
Уравнения (1.4) позволяют выразить напряжения на любой наклонной площадке с нормалью Если наклонная площадка совпадает с поверхностью тела, то составляющие Главные напряжения. Инварианты напряженного состояния При помощи уравнений (1.4) можно вычислить напряжения на любой наклонной площадке в любой точке внутри тела, если известны составляющие напряжения Равнодействующая составляющих напряжения
Разложим полное напряжение на две составляющих — по нормали к площадке и в ее плоскости (соответственно нормальное и касательное напряжения). Нормальное напряжение равно сумме проекций составляющих полного напряжения, параллельных координатным осям, на направление нормали:
Подставляя значения из (1.4), получим
Выражение (1.7) позволяет определять нормальные напряжения на любой наклонной площадке с помощью шести составляющих напряжений на трех площадках, параллельных координатным плоскостям. При этом касательные напряжения на этой площадке будут
Формула (1.8) дает величину касательного напряжения, но не позволяет определить его направление в плоскости площадки. Определим составляющую касательного напряжения в плоскости площадки с нормалью
Искомое касательное напряжение равно сумме проекций составляющих напряжений Подставим в это выражение составляющие напряжения из (1.4):
Выражение (1.10) позволяет определить касательные напряжения на любой наклонной площадке в заданном направлении с помощью шести составляющих напряжений на трех площадках, параллельных координатным плоскостям. Площадка, на которой касательные напряжения равны нулю, называется главной. Для такой площадки ( Из условия Сравнивая эти соотношения с (1.4), получим:
Из аналитической геометрии известно соотношение между направляющими косинусами:
Уравнения (1.11) и (1.12) содержат четыре неизвестных: главное напряжение и три его направляющих косинуса. Преобразуем (1.11) к виду
Эта система имеет ненулевое решение (нулевое решение невозможно в силу (1.11)) тогда и только тогда, когда ее определитель равен нулю: Раскрывая определитель и группируя по степеням
или
где
Решение уравнения (1.14) всегда дает три действительных корня. Наибольший по алгебраическому значению корень обозначается через
Подставляя значение одного из главных напряжений в (1.13), можно найти направляющие косинусы Обозначим два главных напряжения через
Умножим уравнения (1.16) на Т.к. Аналогично можно доказать ортогональность главных площадок, на которых действуют другие пары главных напряжений. Таким образом, в каждой точке тела можно выделить по крайней мере три главных площадки, которые взаимно перпендикулярны друг другу. Величины главных напряжений не зависят от положения координатных осей Если их выразить через главные напряжения (а для этого в (1.15) нужно касательные напряжения принять равными нулю), то получим
В теории напряжений инварианты рассматриваются как основные характеристики напряженного состояния тела в данной точке.
Изгиб прямого бруса: построение эпюр поперечных сил и изгиб моментов (правила построения и контроля эпюр; эпюры при нагружении однопролетной балки сосредоточ силой; эпюры при нагружении однопролетной балки распредел нагрузкой) 1)сосредоточ сила, прилож на конце консоли дает на эп Q скачек на велич силы, а на эп М наклон линию 2) на участках где прилож равномерно распредел нагрузка, эп Q всегда наклонная линия, а эп М квадратич парабола. Эп М на встречу стрелкам, как зонтик.
1) Сосред сила прилож к балке(посреди) на Q дает скачек на велич силы, а на М излом выпуклостью на встречу силе
2) см вопр 5 3) сечение в кот эп Q пересек ось, эп М приним экстимальное значение
0) Определ. реакции опор и считаем число учстков 1) строим эпюры поперечных сил и изгибающих моментов и на эпюре изгиб моментов находи опасные моменты. Под опасным понимается сечение в которых изгиб момент принимает макс. Значение, это справедливо для изотропных и анизотропных материалов с симметричным сечением. 2) Производим расчет по формуле Для анизотропных симметричных материалов в качесвте допуск. Напряжения берется наименьшее. Для нессиметр. Анизотропных материалов надо производить отдельно расчет, как по допускаемым напряжениям сжатия и на разжатие.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.227.125 (0.01 с.) |

 (рис.1.2) определяется нормалью
(рис.1.2) определяется нормалью  с направляющими косинусами
с направляющими косинусами
 Обозначим площадь наклонной площадки через
Обозначим площадь наклонной площадки через  и свяжем с ней площади остальных граней тетраэдра:
и свяжем с ней площади остальных граней тетраэдра: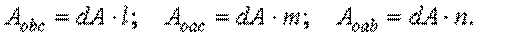
 а на наклонной — силы от трех составляющих полного напряжения
а на наклонной — силы от трех составляющих полного напряжения 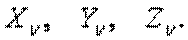 Кроме того, по всему объему тетраэдра действуют составляющие
Кроме того, по всему объему тетраэдра действуют составляющие  объемной силы.
объемной силы.
 получим
получим


 через шесть направляющих напряжений, параллельных координатным плоскостям.
через шесть направляющих напряжений, параллельных координатным плоскостям. полного напряжения соответствуют составляющим внешних сил, действующих на поверхности тела. Тогда уравнения (1.4) будут называться условиями на поверхности тела и свяжут внешние силы с внутренними.
полного напряжения соответствуют составляющим внешних сил, действующих на поверхности тела. Тогда уравнения (1.4) будут называться условиями на поверхности тела и свяжут внешние силы с внутренними. по трем взаимно перпендикулярным площадкам, параллельным координатным плоскостям.
по трем взаимно перпендикулярным площадкам, параллельным координатным плоскостям. на наклонной площадке называется полным напряжением на этой площадке и определяется как геометрическая сумма
на наклонной площадке называется полным напряжением на этой площадке и определяется как геометрическая сумма



 с направляющими косинусами
с направляющими косинусами 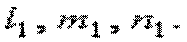 Направления
Направления 
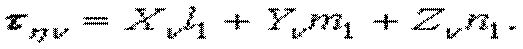

 ) из (1.8) следует
) из (1.8) следует  т.е. на главной площадке полное напряжение совпадает с нормальным как по величине, так и по направлению.
т.е. на главной площадке полное напряжение совпадает с нормальным как по величине, так и по направлению. , спроектируем его на координатные оси и найдем составляющие главного напряжения, параллельные координатным осям:
, спроектируем его на координатные оси и найдем составляющие главного напряжения, параллельные координатным осям:




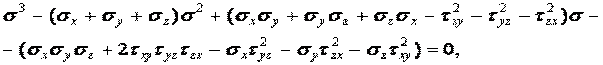


 наименьший —
наименьший —  Таким образом
Таким образом
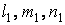 соответствующей главной площадки.
соответствующей главной площадки. ,
,  , а их направляющим косинусам придадим значения с соответствующими индексами и дважды запишем уравнения (1.13):
, а их направляющим косинусам придадим значения с соответствующими индексами и дважды запишем уравнения (1.13):
 соответственно и сложим их:
соответственно и сложим их:
 то получаем условие ортогональности главных площадок, на которых действуют
то получаем условие ортогональности главных площадок, на которых действуют 

 следовательно, корни кубического уравнения (1.14) не зависят от выбора координатной системы и коэффициенты этого уравнения должны сохранять постоянные значения при преобразовании осей, т.е. они являются инвариантами, поэтому величины
следовательно, корни кубического уравнения (1.14) не зависят от выбора координатной системы и коэффициенты этого уравнения должны сохранять постоянные значения при преобразовании осей, т.е. они являются инвариантами, поэтому величины  называются соответственно первым, вторым и третьим инвариантами напряженного состояния.
называются соответственно первым, вторым и третьим инвариантами напряженного состояния.






