Распределение напряжений в грунтах (основные случаи)

σ_z = P*(α+sinα*cos2β)/π = P*K_z

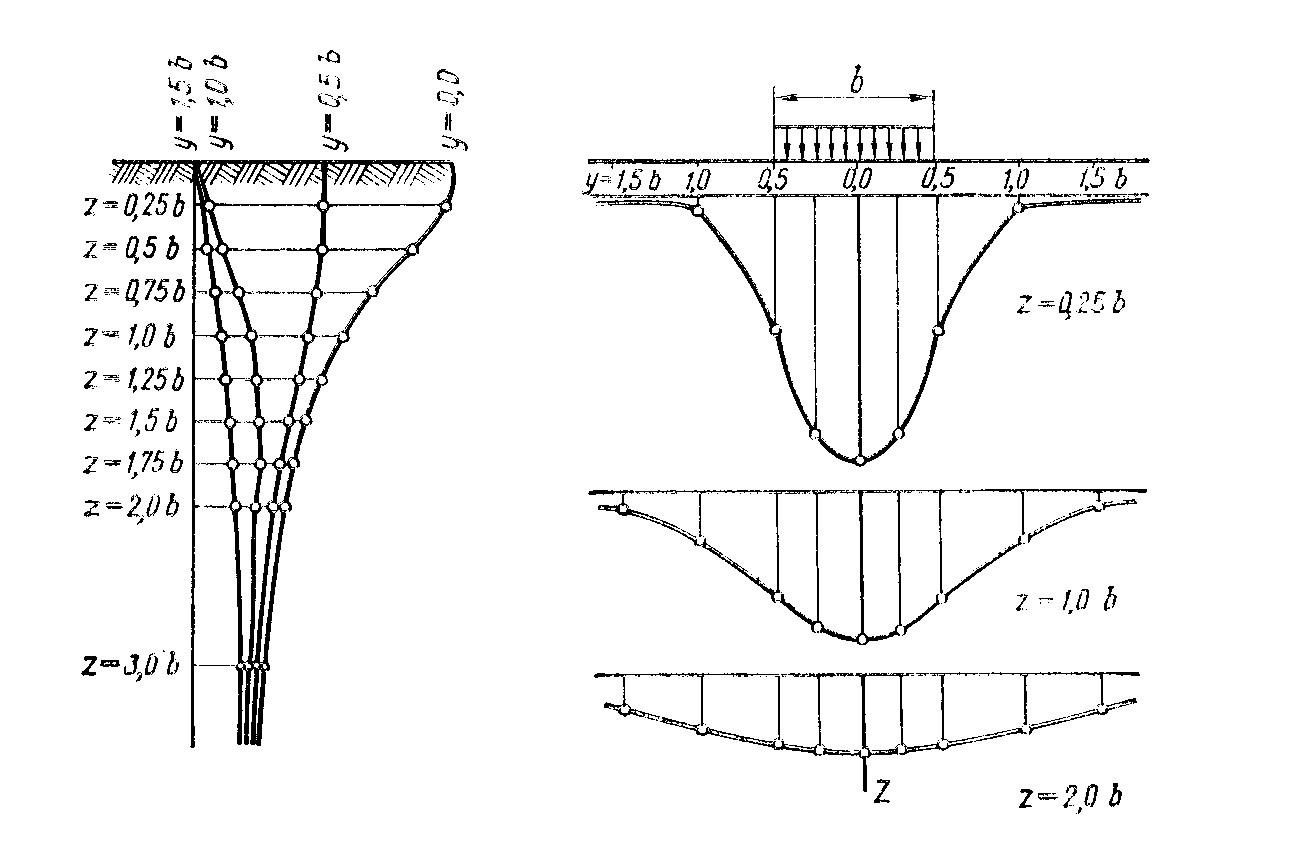
σ_y = P*(α-sinα*cos2β)/ π = P*K_y

τ = P*(sinα*cos2β)/ π = P*K_yz

K= f(z/b, y/b)

Использую табл. и фор-лы можно построить эпюры напряжений по

 

Главные напряжения, т.е. наибольшие и наименьшие нормаль­ные напряжения, будут для площадок, расположенных по вертикаль­ной оси симметрии нагрузки. Действительно, для таких площадокугол β' = -α/2и, след-но, угол β = α/2 - α/2 = 0.

Тогда сдвигающее напря­жение будет равно τ = 0, т. е. площадки будут главными.

Можно показать, что главными площадками будут также площадки, расположенные по биссектрисам углов видимости и площадкам, им перпендикулярным.

Величину главных напряжений, полагая в них β = 0:

σ₁ = P*(α+sinα)/π

σ₂ = P*(α-sinα)/ π

Эти формулы весьма часто применяют при оценке напряжен­ного состояния в основаниях сооружений, особенно предельного.

Они дают также возможность построить эллипсы напряжений для различных точек напряженного линейно деформируемого полупрост­ранства, наглядно иллюстрирующих изменение напряже­ний в грунте под полосообразной нагрузкой.

 

При определении напряжений в основаниях сооружений массива грунта обычно рассматривают как полупространство 0 ≤ z < ∞, ограниченное горизонтальной плоскостью z = 0. Грунт считают находящимся в сложном напряженно-деформированном состоянии и линейно-деформированном, поэтому для него справедливо основное положение закона Гука — линейность связи между напряжениями и деформациями.

Однако при действии внешних сил с давлениями, превышающими структурную прочность грунта, возникают не только упругие, но и значительно большей величины остаточные (пластические) деформации.

Напряжения в массивах грунтов возникают как под действием внешних нагрузок, так и от собственного веса грунта. Знание напряжений необходимо для расчетов деформаций грунтов, обусловливающих осадки и перемещения зданий и сооружений для оценки прочности, устойчивости грунтов и давления на ограждения.

Без учета распределения напряжений в грунте невозможно, например, рассчитать осадки насыпей, устоев мостов, акведуков, лотков, фундаментов искусственных и других сооружений.

Распределение напряжений в грунтовой толще зависит от следующих факторов: характера и режима нагружения массива, инженерно-геологических и гидрогеологических особенностей площадки строительства, состава и физико-механических свойств грунтов.

Давление от нагрузки, приложенной к поверхности грунтового массива, передается в грунте частицами или структурными агрегатами через точки контакта, распределяясь по мере углубления в грунт на все большую площадь.

При оценке напряжений, действующих в грунтах, реальные силы, приложенные к отдельным грунтовым частицам, заменяют воображаемыми силами, распределенными по всему объему или сечению грунтового массива.

Величину этих сил, отнесенных к единице площади сечения массива, и принимают условно за величину напряжений в грунте.

Формирование напряжений в грунтовой толще происходит не мгновенно при приложении нагрузки, а может развиваться весьма длительное время. Это связано со скоростью проектирования деформаций и особенно сильно проявляется в глинистых грунтах, где процессы фильтрационной консолидации (консолидация — процесс уплотнения грунта по мере удаления воды из его пор) и ползучести развиваются очень медленно.

Изучение напряженного состояния грунта можно проводить по двум направлениям:

· экспериментальным путем, измеряя непосредственно давления в грунте при помощи специального оборудования;

· теоретическим путем, используя методы теории упругости, так как здесь мы имеем дело с объемным напряженным состоянием грунтов.

Работа грунта основания существенно отличается от работы материала строительной конструкции, сооружений и т.д. Отличия состоят в следующем:

· грунты имеют малую прочность и большую деформируемость по сравнению с материалами конструкций; прочность их в десятки и сотни раз больше по сравнению с грунтом основания, а деформируемость, наоборот, меньше;

· деформация грунта во времени при постоянной нагрузке возрастает (например, для глинистых грунтов процессы консолидации и ползучести) (рис. 6.2).

Рис. Деформация грунта во времени

Как было сказано выше, деформация глинистых грунтов может длиться годами и даже десятки лет;

· неоднородность грунтов и их свойств в основании фундаментов, а следовательно, прочности и деформируемости (понятие анизотропность), т.е. неодинаковые свойства грунтов в различных направлениях;

· неоднородность напряжений в грунтовой толще в естественных условиях и сложность их изменений под действием внешней нагрузки;

· различие закономерностей изменения напряженного состояния грунтов, однородных по составу, но при различной величине внешней нагрузки (график Герсеванова).