
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пассивные дифференцирующие цепиСтр 1 из 9Следующая ⇒
10, 11. Единичная ступенчатая функция. Единичная импульсная функция Единичная ступенчатая функция (синонимы: единичная функция, единичный скачок, единичное ступенчатое воздействие, функция включения, функция Хевисайда) изображена на рис. 3.1, а
а) б) в) Математическая запись единичной ступенчатой функции
Единичная импульсная функция (синонимы: единичный импульс, дельта-функция
Выражения (3.4) и (3.5) описывают фильтрующее (стробирующее) свойство функции Единичная ступенчатая функция и единичная импульсная функция относятся к семейству разрывных или особых функций и используются для идеализированного представления сигналов. Эти сигналы, часто называемые в теории цепей единичный скачок напряжения и единичный импульс, обычно выбираются в качестве типового внешнего воздействия (возмущения), приложенного ко входу цепи (системы), при котором переходный процесс носит наиболее неблагоприятный характер. Кроме того, при помощи интеграла Дюамеля и интеграла свёртки они позволяют вычислить реакцию цепи на любое внешнее возмущение. Пример 3.6
На входе цепи (рис. 3.8) действует экспоненциальное напряжение
Рис. 3.8 Найти напряжение на индуктивности
Используя (3.16), найдём
25,
27,
28,
29, Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону. Действующие значения несинусоидального тока и несинусоидального напряжения. По определению, квадрат действующего значения тока I выражают через мгновенное значение тока i следующим образом:
Поэтому
Следовательно, действующее значение несинусоидального тока равно корню квадратному из суммы квадратов постоянной составляющей тока и действующих значений отдельных гармоник. От углов сдвига фаз j действующее значение тока не зависит.
Активная и полная мощности несинусоидального тока.
Подставить эти ряды под знак интеграла и проинтегрировать, то можно получить
Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник.
где
30, Единичная ступенчатая функция (синонимы: единичная функция, единичный скачок, единичное ступенчатое воздействие, функция включения, функция Хевисайда) Законы коммутации Ток в индуктивности и напряжение на ёмкости в момент коммутации не могут изменяться скачком, а являются непрерывными функциями времени, т.е.
На основании первого закона коммутации,
На рис. 1.2 б показан постепенный, непрерывный процесс установления тока в цепи после замыкания ключа S.
На рис. 1.3 поясняется второй закон коммутации.
В момент переключения в цепи при t=0 должен выполняться второй закон коммутации
С физической точки зрения законы коммутации являются частными проявлениями общего закона природы – закона непрерывности энергии. Энергия магнитного поля, запасённая в индуктивности Заметим, что ток в ёмкости и напряжение на индуктивности не являются носителями энергии, поэтому законам коммутации не подчиняются и могут изменяться скачком. Малый сигнал. В тех случаях когда изменение токов и напр. Нелин. элементов происходит в окресности некот. Ра. точки О. на узком участке ВАХ достаточно ограничиться аппроксимацией ВАХ лишь в окрестности выбранной раб. точки. Пусть I0, U0 ток и напр. в раб. точке лежащей на ВАХ линейного элемента i=f(u). Значение тока i соответствует нек. новому знач. напр u можно представить в виде ряда Тейлора
Если приращение напр.
т.е. ВАХ линиаризирован в близи раб. точки. Такой режим назыв. режимом малого сигнала. I0 – ток покоя;
1. В режиме малого сигнала Rст и rдиф рассматриваются как линейные, а нелинейность цепи проявляется при выборе рабочей точки от кот. зависит Rст и rдиф. 2. В режиме малого сигнала отдельно по постоянному и переем. току. Сопр. пост. току рассматривается как статич. а переем. току как диф. Результат представляют в виде суперпозиций решений для перемен тока. Большой сигнал: В режиме большого сигнала постоянная составляющая тока отличается от тока покоя и переменная составляющая содержит гармоники высших порядков, причем амплитуда первой гармоники токов Im1 не пропорциональна Um1 и раздельный анализ цепи по постоянному и переменному току становится невозможен.
37, РАСЧЁТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ОПЕРАТОРНЫМ МЕТОДОМ Преобразование Лапласа и его свойства Основой операторного метода является интегральное преобразование Лапласа
Что касается ограничений, налагаемых на Найдём изображения для простейших функций времени (напряжений). 1.
2.
4. откуда 5. Подробные таблицы изображений функций приведены в [1,4,13]. Рассмотрим без вывода два важных свойства преобразования Лапласа. 1. Теорема дифференцирования. Изображение первой производной функции равно изображению функции, умноженному на
В частном случае, когда Теорема интегрирования. Изображение интеграла функции равно изображению этой функции, делённому на
Пассивные дифференцирующие цепи Линейные пассивные четырёхполюсники при определённых условиях могут использоваться для получения сигналов требуемой формы. Наиболее широкое применение получили четырёхполюсники, называемые д и ф ф е р е н ц и р у ю щ и м и и и н т е г р и р у ю щ и м и ц е п я м и. У первых напряжение на выходе приблизительно пропорционально производной, у вторых - интегралу от входного напряжения. Простейшие дифференцирующие цепи изображены на рис. 4.1, а и 4.1 б.
Изображение напряжения на выходе обеих схем
Четырёхполюсник с передаточной функцией (4.1) и (4.2) не является дифференцирующим звеном, однако при выполнении условия
и в соответствии с теоремой дифференцирования (2.11),
т.е. цепи на рис. 4.1 и 4.2 будут практически дифференцирующими. Точность дифференцирования зависит от степени выполнения неравенства (4.4) или при В другом предельном случае при При исследовании переходных процессов в цепях при воздействии импульсных сигналов удобно верхнюю граничную частоту спектра выразить через длительность входного импульса
Теоретически спектр импульса любой формы является бесконечным, однако на практике его ограничивают диапазоном частот, в пределах которого сосредоточена подавляющая часть энергии сигнала. Так, спектр прямоугольного импульса ограничивают частотой
или Таким образом, с учётом формулы (4.8) условие точного дифференцирования
Формула (4.10) применима для периодической последовательности прямоугольных импульсов, а также для сигналов амплитудно-импульсной модуляции (АИМ), так как ширина их спектра определяется только длительностью импульсов Теоретически постоянная времени цепи Пример 4.1
В примере 3.5 рассчитан ток в цепи. Выражения для выходного напряжения в схеме (рис. 4.1 а) имеют вид при При
Формулы (4.11) и (4.12) и графики RL-цепи (рис. 4.1 б) при Временные диаграммы (рис. 4.2) наглядно показывают преобразование формы сигнала на выходе цепи во всем диапазоне изменения отношения При При
Обратимся к области применения четырехполюсников, приведенных на рис. 4.1 и 4.4. Дифференцирующие цепи, отвечающие условию (4.7)
Длительность выходного импульса
Разделительные цепи, удовлетворяющие неравенству Цепь на рис. 4.1 а используется для разделения переменной и постоянной составляющих сигнала, например в цепях межкаскадной связи в усилителях переменного тока. Импульсный трансформатор на рис. 4.4 применяется в качестве согласующего; для изменения полярности импульсов; обеспечивает гальваническую развязку входной и выходной цепей и т. д. Переходные искажения разделительных четырёхполюсников характеризуются относительным спадом вершины импульса (
Разложив
Сравнивая RC-цепь с RL-цепью (рис. 4.1 а, б), отметим, что конструкция и настройка первой схемы при её реализации проще, чем схемы с индуктивной катушкой, и RC-цепь имеет преимущественное применение. Тем не менее можно привести ряд примеров использования дифференцирующей RL-цепи. Так, в импульсных усилителях применяется простая и эффективная ВЧ индуктивная коррекция, расширяющая полосу пропускания усилительного каскада в области верхних частот и уменьшающая искажения фронта импульса [8]. В импульсной технике находят применение дифференцирующие трансформаторы (пример 4.3).
В схеме интегратора на рис. 4.9 б смещение нуля выходного напряжения из-за разбаланса ОУ, а также наличие входных токов смещения, обусловленных конечным значением входного сопротивления, ограничивают максимальную длительность интегрирования, так как с течением времени напряжение ошибки будет нарастать. Из-за конечного значения коэффициента усиления ОУ напряжение на выходе интегратора изменяется по экспоненциальному закону, а не строго линейно (при интегрировании перепада напряжения), однако при этом постоянная времени экспоненты и выходное напряжение приблизительно в На практике применяют модифицированные схемы дифференцирующего устройства и интегратора (рис. 4.10 а, б).
Такой четырёхполюсник, представляющий собой интегродифференцирующее звено, можно использовать в качестве полосового фильтра. Улучшенная схема интегратора показана на рис. 4.10 б. Резисторы Интеграторы широко применяют при создании генераторов линейно изменяющегося и синусоидального напряжений, точных фазосдвигающих устройств, в качестве ARC - фильтров нижних частот и др. Изображение напряжения на выходе обеих схем
Четырёхполюсник с передаточной функцией (4.1) и (4.2) не является дифференцирующим звеном, однако при выполнении условия
и в соответствии с теоремой дифференцирования (2.11),
т.е. цепи на рис. 4.1 и 4.2 будут практически дифференцирующими. Точность дифференцирования зависит от степени выполнения неравенства (4.4) или при В другом предельном случае при При исследовании переходных процессов в цепях при воздействии импульсных сигналов удобно верхнюю граничную частоту спектра выразить через длительнь входного импульс Теоретически спектр импульса любой формы является бесконечным, однако на практике его ограничивают диапазоном частот, в пределах которого сосредоточена подавляющая часть энергии сигнала. Так, спектр прямоугольного импульса ограничивают частотой или 4
. Закон Ома для участка цепи, не содержащего источника ЭДС: Устанавливает связь между током и напряжением на этом участке. Uab=IR Закон Ома для участка цепи, содержащего источник ЭДС. Обобщенный закон Ома: Закон (правило) Ома для участка цепи содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов концах участка цепи и имеющейся на этом участке ЭДС. 2) сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов. Второй закон Кирхгофа алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. R и некоторую мнимую часть jX: Закон Ома в операторной форме. Внутренние ЭДС. На
Перейдём к изображениям:
Первый закон Кирхгофа в операторной форме: 1) алгебраическая сумма мгновенных значений токовсходящихся в любом узле схемы, равна нулю:
Второй закон Кирхгофа в операторной форме:
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.163 (0.119 с.) |
 (3.1)
(3.1)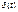 , единичное импульсное воздействие, функция Дирака) определяется как производная по времени от единичной ступенчатой функции
, единичное импульсное воздействие, функция Дирака) определяется как производная по времени от единичной ступенчатой функции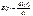 (3.2)
(3.2) 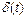 не является функцией в обычном смысле, а рассматривается как обобщённая, обладающая интегральными свойствами
не является функцией в обычном смысле, а рассматривается как обобщённая, обладающая интегральными свойствами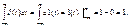 (3.3)Единичная импульсная функция- чётная функция, равная нулю при всех значениях
(3.3)Единичная импульсная функция- чётная функция, равная нулю при всех значениях  , кроме точки
, кроме точки  , в которой она имеет бесконечное значение (рис. 3.1, б); площадь
, в которой она имеет бесконечное значение (рис. 3.1, б); площадь  равна единице. Так как
равна единице. Так как  везде, кроме
везде, кроме  ,то
,то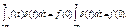 (3.4)В бесконечно малой окрестности точки
(3.4)В бесконечно малой окрестности точки  непрерывная функция
непрерывная функция  постоянна и равна
постоянна и равна  ; вынося
; вынося  за знак интеграла и используя формулу (3.3), получим (3.4). Можно также записать, что
за знак интеграла и используя формулу (3.3), получим (3.4). Можно также записать, что  (3.5)где
(3.5)где 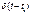 -единичная импульсная функция, смещённая на время
-единичная импульсная функция, смещённая на время 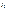 (рис. 3.1, в).
(рис. 3.1, в). .
.

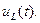
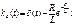
 , где
, где 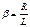
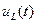

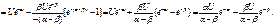 (3.18)
(3.18)



 26,
26,



















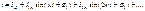 Если ток
Если ток 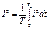
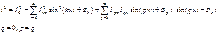 то
то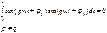 но
но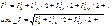
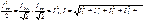 Так как амплитуда k-гармоники тока Ikm в Ö2 раз больше действующего значения тока k-гармоники Ik, то
Так как амплитуда k-гармоники тока Ikm в Ö2 раз больше действующего значения тока k-гармоники Ik, то Аналогично, действующее значение несинусоидального напряжения U равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений отдельных гармоник:
Аналогично, действующее значение несинусоидального напряжения U равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений отдельных гармоник:
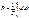 Под активной мощностью P несинусоидального тока понимают среднее значение мгновенной мощности за период первой гармоники:
Под активной мощностью P несинусоидального тока понимают среднее значение мгновенной мощности за период первой гармоники: Если представить напряжение u и ток i рядами Фурье:
Если представить напряжение u и ток i рядами Фурье:
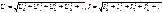 Полная мощность S равна произведению действующего значения несинусоидального напряжения на действующее значение несинусоидального тока: S=U*I
Полная мощность S равна произведению действующего значения несинусоидального напряжения на действующее значение несинусоидального тока: S=U*I
 Равенства (1.1) и (1.2) выражают аналитически соответственно первый и второй законы коммутации.
Равенства (1.1) и (1.2) выражают аналитически соответственно первый и второй законы коммутации. В схеме на рис. 1.2 а происходит коммутация в цепи постоянного тока, содержащей индуктивность. Ток в цепи до коммутации
В схеме на рис. 1.2 а происходит коммутация в цепи постоянного тока, содержащей индуктивность. Ток в цепи до коммутации  ; ток в установившемся режиме после окончания переходного процесса
; ток в установившемся режиме после окончания переходного процесса 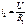 .
.
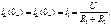
 В схеме на рис. 1.3 а за время переходного процесса напряжение на ёмкости непрерывно изменяется от значения
В схеме на рис. 1.3 а за время переходного процесса напряжение на ёмкости непрерывно изменяется от значения  до
до  (рис. 1.3 б).
(рис. 1.3 б).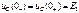 .
. , и энергия электрического поля, запасённая в ёмкости
, и энергия электрического поля, запасённая в ёмкости  , не могут изменяться скачком. Действительно, скачкообразное изменение
, не могут изменяться скачком. Действительно, скачкообразное изменение  или
или  влечёт за собой скачкообразное изменение
влечёт за собой скачкообразное изменение  или
или  . В этом случае мгновенные мощности в индуктивности
. В этом случае мгновенные мощности в индуктивности  в ёмкости
в ёмкости  равны бесконечности, что лишено физического смысла, так как реальные источники энергии не могут развивать бесконечно большую мощность. С другой стороны, если допустить, что в момент коммутации ток
равны бесконечности, что лишено физического смысла, так как реальные источники энергии не могут развивать бесконечно большую мощность. С другой стороны, если допустить, что в момент коммутации ток  (или напряжение
(или напряжение  ) изменяется скачком, то напряжение на индуктивности
) изменяется скачком, то напряжение на индуктивности  (ток в ёмкости
(ток в ёмкости  ) примет бесконечно большое значение, и в цепи не будет выполняться второй (или соответственно первый) закон Кирхгофа.
) примет бесконечно большое значение, и в цепи не будет выполняться второй (или соответственно первый) закон Кирхгофа.
 и тока
и тока  весьма малы, то можно ограничиться полиномом 1й степени
весьма малы, то можно ограничиться полиномом 1й степени
 - статическое вопр. в раб. точке.
- статическое вопр. в раб. точке.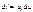
 -диф. сопр. перем. току в режиме малого сигнала
-диф. сопр. перем. току в режиме малого сигнала Нелин. сопр при одновременном воздействии 2х гармонических сигналов различн. частот.
Нелин. сопр при одновременном воздействии 2х гармонических сигналов различн. частот.  ост. с частотами
ост. с частотами  и
и  назыв. колеб. комбинационных частот. Способность нелин. резистивных элем. преобразовывать частоту сигналов с обр. пост. сост. и колебаний кратных и комбинационных частот шиороко используется для получения различных радио устр-в, а именно преобр. частоты, смесителей, модуляторов и демодуляторов. (Выражение выше получается по формуле
назыв. колеб. комбинационных частот. Способность нелин. резистивных элем. преобразовывать частоту сигналов с обр. пост. сост. и колебаний кратных и комбинационных частот шиороко используется для получения различных радио устр-в, а именно преобр. частоты, смесителей, модуляторов и демодуляторов. (Выражение выше получается по формуле 
 , где
, где  – вещественная функция времени (напряжение или ток), удовлетворяющая условиям Дирихле и равная нулю при
– вещественная функция времени (напряжение или ток), удовлетворяющая условиям Дирихле и равная нулю при  , называемая оригиналом;
, называемая оригиналом;  – функция комплексной переменной (комплексной частоты)
– функция комплексной переменной (комплексной частоты)  , называемая изображением по Лапласу. Сокращённо формулу (2.1) (прямое преобразование Лапласа функции
, называемая изображением по Лапласу. Сокращённо формулу (2.1) (прямое преобразование Лапласа функции  ) записывают в виде
) записывают в виде  . Связь между
. Связь между  и
и  обозначают также, как
обозначают также, как 
 , где «
, где « » – знак соответствия.
» – знак соответствия. условиями Дирихле, то реальные напряжения и токи им всегда удовлетворяют.
условиями Дирихле, то реальные напряжения и токи им всегда удовлетворяют. ;
; . Таким образом
. Таким образом 

 .
. ;
; .3.
.3. 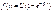

 .
.
 , (2.5)
, (2.5)
 ; (2.6)
; (2.6) 
 . (2.7)
. (2.7)
 . (2.8)6.
. (2.8)6. 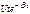
 . (2.9)
. (2.9)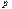 , минус значение функции при
, минус значение функции при  .
.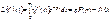 . (2.10)
. (2.10)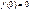 ,
,  . (2.11)
. (2.11) .
. . (2.12)
. (2.12)
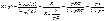 где
где 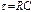 Для цепи на рис. 4.1 б
Для цепи на рис. 4.1 б 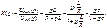 где
где 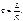
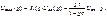 (4.3)
(4.3)
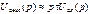 ,
,
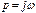 неравенства
неравенства 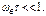 Она тем выше, чем меньше постоянная времени цепи
Она тем выше, чем меньше постоянная времени цепи  (
(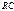 или
или 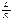 ) и чем ниже
) и чем ниже  - верхняя частота спектра входного сигнала. Выходное напряжение
- верхняя частота спектра входного сигнала. Выходное напряжение  , как следует из выражения (4.6), снижается пропорционально уменьшению
, как следует из выражения (4.6), снижается пропорционально уменьшению 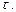
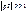
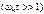 напряжение на выходе цепей рис. (4.1) и (4.2) мало отличается от входного. Такие цепи называют р а з д е л и т е л ь н ы м и.
напряжение на выходе цепей рис. (4.1) и (4.2) мало отличается от входного. Такие цепи называют р а з д е л и т е л ь н ы м и.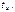
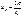 при этом в полосе частот от 0 до
при этом в полосе частот от 0 до 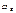 заключено 90,2% его энергии [7]. Примерно такую же ширину спектра имеет другой импульс со скачком – экспоненциальный. У импульсов плавной формы (синусоидальной, треугольной) спектр несколько меньшей протяжённости, однако для ориентировочных оценок граничную частоту спектров импульсов любой формы обычно принимают равной (с запасом)
заключено 90,2% его энергии [7]. Примерно такую же ширину спектра имеет другой импульс со скачком – экспоненциальный. У импульсов плавной формы (синусоидальной, треугольной) спектр несколько меньшей протяжённости, однако для ориентировочных оценок граничную частоту спектров импульсов любой формы обычно принимают равной (с запасом)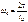 (4.8)
(4.8)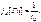 (4.9)
(4.9)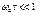 примет вид
примет вид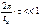 или
или  (4.10)
(4.10)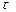 может быть выбрана сколь угодно малой, однако в реальных схемах величина
может быть выбрана сколь угодно малой, однако в реальных схемах величина  ограничена снизу внутренним сопротивлением источника входного сигнала
ограничена снизу внутренним сопротивлением источника входного сигнала  и паразитной ёмкостью нагрузки
и паразитной ёмкостью нагрузки 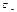 , шунтирующий выход цепи;
, шунтирующий выход цепи; 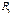 и
и 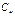 необходимо учитывать при выборе параметров дифференцирующей
необходимо учитывать при выборе параметров дифференцирующей  -цепи (рис. 4.1 а, б) [5].
-цепи (рис. 4.1 а, б) [5]. На вход цепи (рис. 4.1 а) подаётся сигнал в виде одиночного прямоугольного импульса (рис. 4.2 а). Построить временные диаграммы выходного напряжения для различных отношений
На вход цепи (рис. 4.1 а) подаётся сигнал в виде одиночного прямоугольного импульса (рис. 4.2 а). Построить временные диаграммы выходного напряжения для различных отношений  к длительности
к длительности 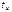 входного импульса.
входного импульса.

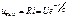 . (4.11)
. (4.11)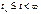
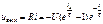 . (4.12)
. (4.12)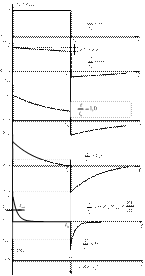 На рис. 4.2 а-е по формулам (4.11) и (4.12) построены кривые
На рис. 4.2 а-е по формулам (4.11) и (4.12) построены кривые 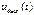 для значений
для значений 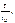 равных: а)
равных: а)  ; б)10; в)1,0; г)0,3; д)0,05; е)0.
; б)10; в)1,0; г)0,3; д)0,05; е)0.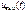 справедливы также для
справедливы также для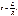
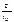 от
от 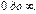
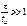 (рис. 4.2 б) цепь является разделительной; её назначение– пропускать сигнал без существенных переходных искажений.
(рис. 4.2 б) цепь является разделительной; её назначение– пропускать сигнал без существенных переходных искажений.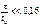 (рис. 4.2 д)
(рис. 4.2 д)  - цепь приближается к дифференцирующей. Чем меньше отношение
- цепь приближается к дифференцирующей. Чем меньше отношение 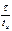 , тем короче экспоненциальные импульсы на выходе цепи в моменты скачков входного напряжения. Результат идеального дифференцирования прямоугольного импульса в виде двух дельта-функций
, тем короче экспоненциальные импульсы на выходе цепи в моменты скачков входного напряжения. Результат идеального дифференцирования прямоугольного импульса в виде двух дельта-функций  показан на рис. 4.2 е.
показан на рис. 4.2 е.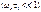 , обычно используют для получения коротких импульсов с крутыми фронтами, а не для аналогового дифференцирования в установившемся режиме. Они работают в режиме наибольших переходных искажений, поэтому более точное название таких цепей укорачивающие (о б о с т р я ю - щ и е), а в импульсной технике – у с к о р я ю щ и е (ф о р с и р у ю щ и е) цепи.
, обычно используют для получения коротких импульсов с крутыми фронтами, а не для аналогового дифференцирования в установившемся режиме. Они работают в режиме наибольших переходных искажений, поэтому более точное название таких цепей укорачивающие (о б о с т р я ю - щ и е), а в импульсной технике – у с к о р я ю щ и е (ф о р с и р у ю щ и е) цепи.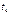 , обычно отсчитываемая на уровне 0,5
, обычно отсчитываемая на уровне 0,5 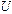 , называется а к т и в н о й (
, называется а к т и в н о й (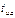 на рис. 4.2 д).
на рис. 4.2 д). Для экспоненциального импульса
Для экспоненциального импульса 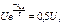 откуда
откуда 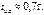
 , где
, где 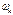 - нижняя частота спектра входного сигнала, предназначены для передачи сигналов через четырёхполюсник с допустимыми переходными искажениями.
- нижняя частота спектра входного сигнала, предназначены для передачи сигналов через четырёхполюсник с допустимыми переходными искажениями.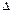 ):
):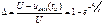 (4.16)
(4.16) в степенной ряд (1.23) и ограничившись двумя членами этого ряда, что справедливо для малых
в степенной ряд (1.23) и ограничившись двумя членами этого ряда, что справедливо для малых 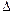 (
(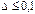 ), получим приближённую формулу для
), получим приближённую формулу для 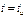
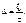 В примере 4.1 на рис. 4.2 б показан спад вершины импульса для случая
В примере 4.1 на рис. 4.2 б показан спад вершины импульса для случая 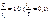 При этом
При этом 
 и погрешность формулы (4.16) составляет 5%. Для сигнала на рис. 4.2 в
и погрешность формулы (4.16) составляет 5%. Для сигнала на рис. 4.2 в 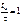 формула (4.17) не пригодна:
формула (4.17) не пригодна: 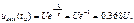
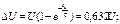
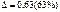 .
. Передаточная функция идеального дифференцирующего усилителя не может быть реализована из-за ограниченной полосы пропускания и конечного коэффициента усиления реального ОУ. Кроме того, схема на рис. 4.9 а может самовозбудиться из-за спада коэффициента усиления ОУ на высоких частотах и дополнительных фазовых сдвигов, вносимых цепью ОС [5]. Уменьшение
Передаточная функция идеального дифференцирующего усилителя не может быть реализована из-за ограниченной полосы пропускания и конечного коэффициента усиления реального ОУ. Кроме того, схема на рис. 4.9 а может самовозбудиться из-за спада коэффициента усиления ОУ на высоких частотах и дополнительных фазовых сдвигов, вносимых цепью ОС [5]. Уменьшение 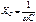 с увеличением частоты приводит к тому, что схема дифференцирующего усилителя имеет высокий коэффициент усиления на верхних частотах, даже за пределами полосы частот полезного сигнала. Поэтому, наряду с ВЧ составляющими спектра входного сигнала, схема усиливает собственные шумы и внешние помехи, которые накладываются на полезный сигнал и искажают его.
с увеличением частоты приводит к тому, что схема дифференцирующего усилителя имеет высокий коэффициент усиления на верхних частотах, даже за пределами полосы частот полезного сигнала. Поэтому, наряду с ВЧ составляющими спектра входного сигнала, схема усиливает собственные шумы и внешние помехи, которые накладываются на полезный сигнал и искажают его. раз больше, а погрешность интегрирования в
раз больше, а погрешность интегрирования в 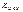 раз меньше, чем у пассивной интегрирующей цепи при тех же номиналах R и C.
раз меньше, чем у пассивной интегрирующей цепи при тех же номиналах R и C. Чтобы избежать проявления нежелательных свойств четырёхполюсника на рис. 4.9 а, используют скорректированную схему (рис. 4.10 а), которая дифференцирует сигналы до частоты
Чтобы избежать проявления нежелательных свойств четырёхполюсника на рис. 4.9 а, используют скорректированную схему (рис. 4.10 а), которая дифференцирует сигналы до частоты 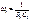 , является усилителем с
, является усилителем с  в полосе частот от
в полосе частот от 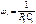 до
до  и интегратором на частотах выше
и интегратором на частотах выше 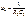 .
.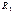 и
и 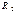 позволяют уменьшить ошибку интегрирования, вызванную разностью входных токов и напряжением смещения нуля ОУ. Для сброса интегратора на нуль (при отсутствии
позволяют уменьшить ошибку интегрирования, вызванную разностью входных токов и напряжением смещения нуля ОУ. Для сброса интегратора на нуль (при отсутствии 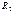 ) перед началом интегрирования конденсатор С кратковременно закорачивают с помощью электронного ключа
) перед началом интегрирования конденсатор С кратковременно закорачивают с помощью электронного ключа 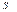 , выполненного на микросхеме или МОП - транзисторе.
, выполненного на микросхеме или МОП - транзисторе. (4.3)
(4.3)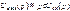 ,
,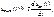
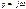 неравенства
неравенства 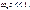 Она тем выше, чем меньше постоянная времени цепи
Она тем выше, чем меньше постоянная времени цепи 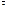 (
( или
или  ) и чем ниже
) и чем ниже 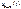 , как следует из выражения (4.6), снижается пропорционально уменьшению
, как следует из выражения (4.6), снижается пропорционально уменьшению 
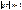
 напряжение на выходе цепей рис. (4.1) и (4.2) мало отличается от входного. Такие цепи называют р а з д е л и т е л ь н ы м и.
напряжение на выходе цепей рис. (4.1) и (4.2) мало отличается от входного. Такие цепи называют р а з д е л и т е л ь н ы м и.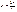 при этом в полосе частот от 0 до
при этом в полосе частот от 0 до 
 Таким образом, с учётом формулы (4.8) условие точного дифференцирования
Таким образом, с учётом формулы (4.8) условие точного дифференцирования  примет вид
примет вид 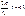 или
или 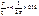 Формула (4.10) применима для периодической последовательности прямоугольных импульсов, а также для сигналов амплитудно-импульсной модуляции (АИМ), так как ширина их спектра определяется только длительностью импульсов
Формула (4.10) применима для периодической последовательности прямоугольных импульсов, а также для сигналов амплитудно-импульсной модуляции (АИМ), так как ширина их спектра определяется только длительностью импульсов 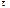 может быть выбрана сколь угодно малой, однако в реальных схемах величина
может быть выбрана сколь угодно малой, однако в реальных схемах величина  ограничена снизу внутренним сопротивлением источника входного сигнала
ограничена снизу внутренним сопротивлением источника входного сигнала  и паразитной ёмкостью нагрузки
и паразитной ёмкостью нагрузки 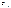 , шунтирующий
, шунтирующий

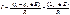 Законы Кирхгофа: 1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю:
Законы Кирхгофа: 1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю: Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.
Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.
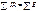 2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю: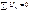 т.е.
т.е. 

 вмс. 8.26 изображена часть сложной разветвленной электрической цепи. Между узлами а и b этой цепи включена ветвь, содержащая R,L, С и источник ЭДС е(t). Замыкание ключа К. в схеме приводит к переходному процессу. До коммутации ток i=i(0_) и напряжение на конденсаторе Uс=Uc(0_). Запишем падение напряжения на участке цепи:
вмс. 8.26 изображена часть сложной разветвленной электрической цепи. Между узлами а и b этой цепи включена ветвь, содержащая R,L, С и источник ЭДС е(t). Замыкание ключа К. в схеме приводит к переходному процессу. До коммутации ток i=i(0_) и напряжение на конденсаторе Uс=Uc(0_). Запишем падение напряжения на участке цепи: 
 на
на  ,
,  на
на 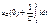 =>
=> 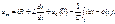
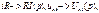
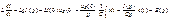 Тогда падение примет вид:
Тогда падение примет вид: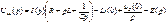 после преоб
после преоб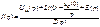

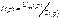
 , т.е.
, т.е.  , а в операторной форме
, а в операторной форме  .
.


