
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Включение RLC-цепи на постоянное напряжение
Требуется найти ток i и Рис. 1.21 напряжения Составим интегродифференциальное уравнение равновесия напряжений в контуре
Свободная составляющая
Как уже отмечалось ранее в § 1.4 характеристическое уравнение (1.45) проще составить, записав для цепи комплексное входное сопротивление
Приравняв Корни уравнения (1.45)
где Решение однородного уравнения (1.44) зависит от вида корней 1. Апериодический случай – корни
Каждый из корней даёт независимое решение, и свободная составляющая напряжения на ёмкости
где A и B – постоянные интегрирования. Переходное напряжение
а переходный ток в контуре
Найдём постоянные интегрирования
Для момента
отку Подставив
Так как в (1.46) Переходные напряжения
Графики переходного процесса для
Рис. 1.22, а
Рис. 1.22, б
Найдём максимум (амплитуду) импульса переходного тока (рис. 1.22, б)
Приравняв эту производную нулю, получим время этого максимума
Подставив 3. Предельный апериодический (критический) случай: корни В этом граничном случае выражение для
Графики переходного процесса для этого случая показаны на рис. 1.25, а, б.
Из формулы (1.66) и графика (рис. 1.25, а) видно, что напряжение В практических случаях представляет интерес амплитуда импульса тока, которым заряжается конденсатор. Приравняв производную Из равенства
При
Контур с добротностью 34. Расчет разветвленных магнитных цепей Расчеты основаны на применении з-нов Кирхгофа для магн. цепей. расчеты обычно ведут граф. аналитическими методами, аналогично расчетам нелинейных эл. цепей. Используется принцип эл.-магн. аналогии.
Прямая задача: Задан поток в воздушном зазоре Ф3. Требуется определить намагничивающий ток. По известному потоку Ф вычисляем индукцию
Поток Обратная задача: Определение всех потоков по заданной МДС. Решается граф. методом пересечений.
36, Нелинейное сопротивление при гармоническом воздействии. Пусть ВАХ Нелин. сопр. аппроксимирован полиномом 1ой степени
1) ток через Нелин. сопр. = сумме гармоник с частотами кратными частоте напр., при этом порядок высшей гармоники = степени полинома n аппроксимирующего ВАХ Нелин. сопр. 2) Нелин. цепь генерирует колеб. частоты кот. отличается от частоты внешнего воздействия.
3) Нелинейность ВАХ цепи явл. причиной нелинейн. искажений например в усилителях переем. тока. Малый сигнал. В тех случаях когда изменение токов и напр. Нелин. элементов происходит в окресности некот. Ра. точки О. на узком участке ВАХ достаточно ограничиться аппроксимацией ВАХ лишь в окрестности выбранной раб. точки. Пусть I0, U0 ток и напр. в раб. точке лежащей на ВАХ линейного элемента i=f(u). Значение тока i соответствует нек. новому знач. напр u можно представить в виде ряда Тейлора
Если приращение напр.
т.е. ВАХ линиаризирован в близи раб. точки. Такой режим назыв. режимом малого сигнала. I0 – ток покоя;
1. В режиме малого сигнала Rст и rдиф рассматриваются как линейные, а нелинейность цепи проявляется при выборе рабочей точки от кот. зависит Rст и rдиф. 2. В режиме малого сигнала отдельно по постоянному и переем. току. Сопр. пост. току рассматривается как статич. а переем. току как диф. Результат представляют в виде суперпозиций решений для перемен тока. Большой сигнал: В режиме большого сигнала постоянная составляющая тока отличается от тока покоя и переменная составляющая содержит гармоники высших порядков, причем амплитуда первой гармоники токов Im1 не пропорциональна Um1 и раздельный анализ цепи по постоянному и переменному току становится невозможен.
37, РАСЧЁТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ОПЕРАТОРНЫМ МЕТОДОМ Преобразование Лапласа и его свойства Основой операторного метода является интегральное преобразование Лапласа
Что касается ограничений, налагаемых на Найдём изображения для простейших функций времени (напряжений). 1.
2.
4. откуда 5. Подробные таблицы изображений функций приведены в [1,4,13]. Рассмотрим без вывода два важных свойства преобразования Лапласа. 1. Теорема дифференцирования. Изображение первой производной функции равно изображению функции, умноженному на
В частном случае, когда Теорема интегрирования. Изображение интеграла функции равно изображению этой функции, делённому на
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.121.160 (0.118 с.) |
 Заданы параметры цепи (рис. 1.21): R, L, C; напряжение U; независимые начальные условия:
Заданы параметры цепи (рис. 1.21): R, L, C; напряжение U; независимые начальные условия: ,
,  (1.41)
(1.41) ,
,  ,
,  .
. . (1.42)Для получения дифференциального уравнения выразим ток i через напряжение
. (1.42)Для получения дифференциального уравнения выразим ток i через напряжение  :
: 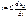 ;
;  (1.43)Общее решение уравнения (1.43) имеет вид
(1.43)Общее решение уравнения (1.43) имеет вид  ;
; 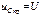 .
. является общим решением однородного уравнения
является общим решением однородного уравнения .(1.44)Соответствующее характеристическое уравнение
.(1.44)Соответствующее характеристическое уравнение или
или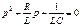 . (1.45)
. (1.45) .
. При
При 
 .
. к 0, получим характеристическое уравнение (1.45).
к 0, получим характеристическое уравнение (1.45). , (1.46)
, (1.46) – коэффициент затухания,
– коэффициент затухания,  – резонансная частота.
– резонансная частота. и
и  . Из (1.46) следует, что корни могут быть вещественными неравными (
. Из (1.46) следует, что корни могут быть вещественными неравными ( ), вещественными равными (
), вещественными равными ( ) и комплексно-сопряжёнными (
) и комплексно-сопряжёнными ( ). Соответственно различают три случая свободного процесса в цепи (рис. 1.21):
). Соответственно различают три случая свободного процесса в цепи (рис. 1.21): – вещественные, отрицательные и неравные
– вещественные, отрицательные и неравные ;
;  или
или  .
. , (1.47)
, (1.47) примет вид
примет вид , (1.48)
, (1.48) . (1.49)
. (1.49)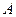 и
и  , используя начальные условия (1.41) и законы коммутации,
, используя начальные условия (1.41) и законы коммутации, ;
;  . (1.50)
. (1.50) из (1.48) и (1.49) следует
из (1.48) и (1.49) следует ;
; ил
ил 
 ;
;  . (1.52)
. (1.52) и
и  в (1.48) и (1.49), получим
в (1.48) и (1.49), получим ; (1.53)
; (1.53) ;
; ,
,  . (1.54)
. (1.54) и
и 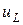 найдём по формулам
найдём по формулам ;
;  .
. построены на рис. 1.22, а, б.
построены на рис. 1.22, а, б.
 .
.

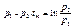
 .
. в формулу (1.54), найдём
в формулу (1.54), найдём  .
. и
и  (1.46) – вещественные, отрицательные и равные,,
(1.46) – вещественные, отрицательные и равные,,  .
. просто получить из формулы (1.57), используя предельный переход при
просто получить из формулы (1.57), используя предельный переход при  и раскрывая неопределённость
и раскрывая неопределённость  по правилу Лопиталя
по правилу Лопиталя
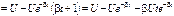 . (1.66)
. (1.66) . (1.67)
. (1.67)

 и
и  . При расчёте по формуле (1.66) напряжение
. При расчёте по формуле (1.66) напряжение  отличается от
отличается от  при
при  на
на  , при
, при  на
на  , при
, при  на
на  . Таким образом, время переходного процесса
. Таким образом, время переходного процесса 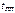 можно считать близким к
можно считать близким к  .
. нулю, найдём
нулю, найдём  и
и  .
. , при котором корни характеристического уравнения становятся равными, находят граничное значение сопротивления
, при котором корни характеристического уравнения становятся равными, находят граничное значение сопротивления 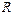 , которое называют критическим,
, которое называют критическим, . (1.66)
. (1.66) переходный процесс имеет апериодический характер, при
переходный процесс имеет апериодический характер, при  процесс становится колебательным. Добротность контура в критическом режиме
процесс становится колебательным. Добротность контура в критическом режиме
 называют колебательным.
называют колебательным.
 , по кривой намагничивания найдем напряженность магн. поля H3 и по формуле
, по кривой намагничивания найдем напряженность магн. поля H3 и по формуле  напряжонность поля в воздушном зазоре. Магнитное напряжение 3й ветви, т.е. м/д узлами a и b
напряжонность поля в воздушном зазоре. Магнитное напряжение 3й ветви, т.е. м/д узлами a и b . Т.к. 2я и 3я ветви соединены параллельно, то и H 2 l 2= U м ab. Вычисляем
. Т.к. 2я и 3я ветви соединены параллельно, то и H 2 l 2= U м ab. Вычисляем  , по кривой намагничивания найдем B 2.
, по кривой намагничивания найдем B 2. , а поток
, а поток  , Вычисляем магн. индукцию
, Вычисляем магн. индукцию 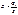 и по кривой намагничивания найдем напряженность магн. поля H 1. По 2му з-ну Кирхгофа, искомая н.с.
и по кривой намагничивания найдем напряженность магн. поля H 1. По 2му з-ну Кирхгофа, искомая н.с.  ;
;

 (1)
(1) Выводы:
Выводы:
 и тока
и тока  весьма малы, то можно ограничиться полиномом 1й степени
весьма малы, то можно ограничиться полиномом 1й степени
 - статическое вопр. в раб. точке.
- статическое вопр. в раб. точке.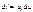
 -диф. сопр. перем. току в режиме малого сигнала
-диф. сопр. перем. току в режиме малого сигнала Нелин. сопр при одновременном воздействии 2х гармонических сигналов различн. частот.
Нелин. сопр при одновременном воздействии 2х гармонических сигналов различн. частот.  ост. с частотами
ост. с частотами  и
и  назыв. колеб. комбинационных частот. Способность нелин. резистивных элем. преобразовывать частоту сигналов с обр. пост. сост. и колебаний кратных и комбинационных частот шиороко используется для получения различных радио устр-в, а именно преобр. частоты, смесителей, модуляторов и демодуляторов. (Выражение выше получается по формуле
назыв. колеб. комбинационных частот. Способность нелин. резистивных элем. преобразовывать частоту сигналов с обр. пост. сост. и колебаний кратных и комбинационных частот шиороко используется для получения различных радио устр-в, а именно преобр. частоты, смесителей, модуляторов и демодуляторов. (Выражение выше получается по формуле 
 , где
, где  – вещественная функция времени (напряжение или ток), удовлетворяющая условиям Дирихле и равная нулю при
– вещественная функция времени (напряжение или ток), удовлетворяющая условиям Дирихле и равная нулю при  , называемая оригиналом;
, называемая оригиналом;  – функция комплексной переменной (комплексной частоты)
– функция комплексной переменной (комплексной частоты)  , называемая изображением по Лапласу. Сокращённо формулу (2.1) (прямое преобразование Лапласа функции
, называемая изображением по Лапласу. Сокращённо формулу (2.1) (прямое преобразование Лапласа функции  ) записывают в виде
) записывают в виде  . Связь между
. Связь между  и
и  обозначают также, как
обозначают также, как 
 , где «
, где « » – знак соответствия.
» – знак соответствия. условиями Дирихле, то реальные напряжения и токи им всегда удовлетворяют.
условиями Дирихле, то реальные напряжения и токи им всегда удовлетворяют. ;
; . Таким образом
. Таким образом 

 .
. ;
; .3.
.3. 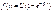

 .
.
 , (2.5)
, (2.5)
 ; (2.6)
; (2.6) 
 . (2.7)
. (2.7)
 . (2.8)6.
. (2.8)6. 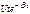
 . (2.9)
. (2.9)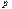 , минус значение функции при
, минус значение функции при  .
.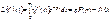 . (2.10)
. (2.10)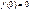 ,
,  . (2.11)
. (2.11) .
. . (2.12)
. (2.12)


