Порядок расчёта переходного процесса

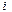Анализ переходного процесса в разветвлённой цепи начинают с составления системы уравнений для мгновенных значений токов и напряжений, используя любой подходящий для расчётов метод (контурных токов, узловых потенциалов, законов Кирхгофа и др.). Если требуется найти какой-либо один ток (или напряжение), то систему исходных дифференциальных уравнений путём исключения остальных переменных приводят к одному уравнению n-го порядка:

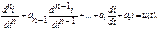Принуждённая составляющая 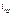зависит от вида приложенного напряжения 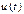– это либо постоянное, либо синусоидальное напряжение; составляющую находят обычными методами расчёта установившегося режима после коммутации.

Физическая причина свободного процесса – несоответствие запаса электромагнитной энергии в реактивных элементах цепи в момент коммутации тому значению, которое должно быть в них после коммутации.

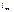Свободный ток представляет общее решение однородного уравнения

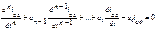.Решение уравнения (1.9) находят в виде

. Подставив экспоненту 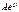и её производные 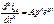в уравнение (1.9), после сокращения 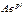получают алгебраическое уравнение степени 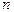, которое называют х а р а к т е р и с т и ч е с к и м у р а в н е н и е м:

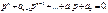Каждый из n корней уравнения (1.11) даёт линейно независимое решение 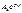; общее решение уравнения (1.9) представляет линейную комбинацию этих решений. Вид корней определяет характер свободного процесса, его функциональную зависимость от времени.

В частном случае, если корни характеристического уравнения вещественные и различные, выражение свободного тока имеет вид

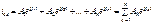,где – постоянные интегрирования.

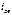Другие варианты возможных решений для рассмотрены ниже в § 1.13.

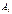Постоянные интегрирования в выражении (1.12) определяют из начальных условий – значений токов и напряжений в цепи при .

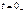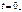Прежде всего из законов коммутации (1.1) и (1.2) находят н е з а в и с и м ы е н а ч а л ь н ы е у с л о в и я (значения), которые справедливы только для тока через индуктивность и для напряжения на ёмкости. Значения остальных токов и напряжений при (з а в и с и м ы е н а ч а л ь н ы е у с л о в и я) определяют по независимым начальным условиям, используя законы Кирхгофа.

Отметим, что порядок дифференциального уравнения (1.8) (порядок цепи) равен общему числу индуктивностей и ёмкостей, для которых можно задать независимые начальные условия. Ввиду того, что решения для свободного тока (или напряжения) в любой ветви цепи имеют стандартную форму (1.10), а корни уравнения (1.11) зависят только от параметров цепи R, L, C, нет необходимости всякий раз составлять и обрабатывать дифференциальные уравнения. Расчёт переходного процесса рекомендуется вести в следующем порядке. Выбрать условно положительные направления токов в ветвях цепи. 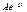Записать для искомого тока общее решение в виде .

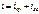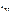Найти в установившемся режиме после коммутации. Составить характеристическое уравнение и найти его корни. Его можно записать по виду дифференциального уравнения (1.9), если последнее известно. Другой, более простой способ его получения состоит в том, что для цепи находят комплексное входное сопротивление 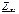, в котором заменяют 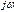на 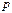, а затем приравнивают к нулю. 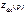можно составить относительно любой ветви цепи, причём источник ЭДС следует условно закоротить, так как его внутреннее сопротивление равно нулю. По виду корней 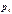характеристического уравнения записать решение для свободного тока 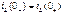(см. § 1.13). Определить независимые начальные условия (1.1) и (1.2) и и, используя их, найти зависимые значения искомых токов (или напряжений) для 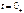по законам Кирхгофа.

Найти постоянные интегрирования. Записать окончательные выражения переходных токов и напряжений. Определить необходимые параметры переходного режима (постоянные времени, время переходного процесса, величину выбросов и др.).