Алгоритмы обработки последовательностей чисел

 

Последовательность значений - это набор однотипных величин, которые вводятся и обрабатываются циклически. Примером последовательности целых чисел может быть следующий набор значений: (2,5,-4,10,1,0). Последовательности значений отличаются от массивов значений тем, что в памяти одновременно все значения последовательности не хранятся. Для обозначения значения последовательности используют одну переменную, в которую на каждом шаге итерации вводится очередное значение последовательности. Отличительной особенностью последовательности является также возможность содержания неопределенного или неизвестного заранее количества ее значений. В этом случае критерием окончания последовательности служит некоторое особое значение, например, ноль.

 

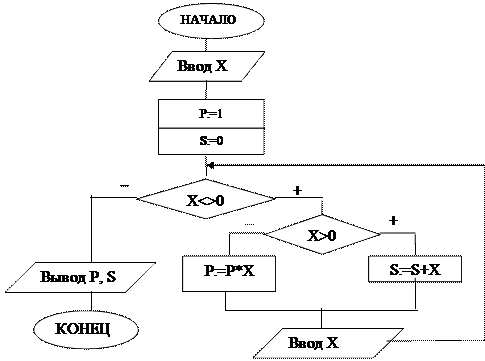
Пример 7. В числовой последовательности определить сумму положительных и произведение отрицательных чисел. Решение представить с использованием циклического алгоритма с предусловием. Признак конца последовательности - значение 0.

Решение. Обозначим за Х переменную, содержащую очередное значение последовательности, за S - сумму положительных значений, за Р - произведение отрицательных значений. Полученный алгоритм приведен на рис. 14. Условие

 

 

для выбора вычислений Х>0. Для вычисления суммы значений воспользуемся реккурентной формулой S=S+X с начальным значением S=0, для вычисления произведения - реккурентной формулой P=P*X с начальным значением Р=1. Условие выхода из цикла неравенство Х<>0.

 

Пример 8. Составить циклический алгоритм с постусловием для определения в последовательности целых чисел количества четных чисел.

 

 

Рис.14. Алгоритм вычисления суммы положительных и произведения отрицательных значений числовой последовательности

Решение. Обозначим за Х переменную, содержащую очередное значение последовательности, за K - количество четных значений (рис. 15). Условие для выбора четных значений Х mod 2=0 (остаток при делении Х на 2 равен 0). Для вычисления количества значений воспользуемся реккурентной формулой К=К+1 с начальным значением К=0.

 

Рис. 15. Алгоритм определения количества четных чисел в последовательности значений

 

 

Задание №3

Составить визуальные циклические алгоритмы для следующих задач обработки последовательности значений (номер варианта определяется по последней цифре учебного шифра).

 

1. В последовательности чисел подсчитать произведение чисел, кратных 3.

2. В последовательности чисел сравнить,что больше сумма положительных или произведение отрицательных.

3. В последовательности чисел определить предпоследнее отрицательное число.(При решении введите дополнительную переменную для хранения предпоследнего отрицательного числа).

4. В последовательности целых положительных чисел определить

максимальное число (Рекомендуем реализовать такой алгоритм:

Вводим Х

mах=Х

Цикл с постусловием

а. Если элемент Х > max

то max:=Х (значение этого элемента);

б. Вводим новый элемент последовательности Х.

Условие выхода из цикла Х=0)

5. В последовательности целых чисел определить третье положительное число и подсчитать количество цифр в нем.

6. В последовательности чисел подсчитать произведение чисел, кратных 8.

7. В последовательности чисел сравнить,что больше модуль суммы отрицательных или сумма положительных значений.

8. В последовательности чисел определить предпоследнее четное число.(При решении введите дополнительную переменную для хранения предпоследнего четного числа).

9. В последовательности чисел определить предпоследнее нечетное число. (При решении введите дополнительную переменную для хранения предпоследнего нечетного числа)

0. В последовательности чисел подсчитать произведение чисел, кратных 10.

 

 

Задание на контрольную работу часть2