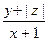Часть 2. Математические операции Excel

Задание на контрольную работу

Часть 1. Алгоритмы

оформляем в Word+титульный лист!!!!

Часть 2. Математические операции Excel

Оформляем в Excel

 

Часть 1. Тема: «ОСНОВЫ АЛГОРИТМИЗАЦИИ»

 

Слово «алгоритм» появилось в 9-м веке и связано с именем математика Аль-Хорезми, который сформулировал правила выполнения четырех арифметических действий над многозначными числами.

В настоящее время понятие алгоритма - одно из фундаментальных понятий науки информатика. С одной стороны алгоритм является предметом изучения такой отрасли математики как теория алгоритмов, с другой стороны в информатике существует неформальное определение алгоритма, и алгоритмизация выступает в качестве общего метода информатики.

Алгоритм – это точно определенная последовательность действий для некоторого исполнителя, выполняемых по строго определенным правилам и приводящих через некоторое количество шагов к решению задачи.

Исполнитель алгоритмов определяет элементарные действия, из которых формируется алгоритм. Отдельные действия, составляющие алгоритм, называются операциями. При этом под операцией понимается как какое-то единичное действие, например, сложение, так и группа взаимосвязанных действий.

Основными особенностями любого алгоритма являются решение задачи в обобщенном виде и возможность выполнять действия по решению задачи для конкретных значений (не только человеку, но и различным техническим устройствам (исполнителям)). Основным исполнителем несложных алгоритмов является человек. Достаточно вспомнить последовательность действий для решения систем линейных уравнений, вычисления корней уравнений.

При решении сложных задач исполнителем является ЭВМ и составление алгоритма решения задачи является необходимым этапом, детализирующим метод решения для дальнейшего программирования. Программа осуществляет еще более глубокую детализацию решения и его визуализацию.

Свойства алгоритма:

Определенность – выполнив очередное действие, исполнитель должен точно знать, что ему делать дальше.

Дискретность – прежде, чем выполнить определенное действие, надо выполнить предыдущее.

Массовость – по одному и тому же алгоритму решаются однотипные задачи и неоднократно.

Понятность – алгоритм строится для конкретного исполнителя человеком и должен быть ему понятен. Это облегчает его проверку и модификацию при необходимости.

Результативность – алгоритм всегда должен приводить к результату.

 

Алгоритм моделирует решение задачи в виде точно определенной последовательности действий для некоторого исполнителя по преобразованию исходных данных в результирующие. Процесс составления алгоритмов называют алгоритмизацией.

Алгоритм, реализующий решение задачи, можно представить различными способами: с помощью графического или текстового

описания, в виде таблицы значений. Графический способ представления алгоритмов имеет ряд преимуществ благодаря визуальности и явному отображению процесса решения задачи. Алгоритмы, представленные графическими средствами, получили название визуальные алгоритмы. Текстовое описание алгоритма является достаточно компактным и может быть реализовано на абстрактном или реальном языке программирования в виде программы для ЭВМ. Таблицы значений представляют алгоритм неявно, как некоторое преобразование конкретных исходных данных в выходные. Табличный способ описания алгоритмов может быть с успехом применен для проверки правильности функционирования разработанного алгоритма на конкретных тестовых наборах входных данных, которые вместе с результатами выполнения алгоритма фиксируются в "таблицах трассировки".

Таким образом, все три способа представления алгоритмов можно считать взаимодополняющими друг друга. На этапе проектирования алгоритмов наилучшим способом является графическое представление, на этапе проверки алгоритма - табличное описание, на этапе применения - текстовая запись в виде программы.

Общими правилами при проектировании визуальных алгоритмов являются следующие:

· В начале алгоритма должны быть блоки ввода значений входных данных.

· После ввода значений входных данных могут следовать блоки обработки и блоки условия.

· В конце алгоритма должны располагаться блоки вывода значений выходных данных.

· Связи между блоками указываются направленными или ненаправленными линиями.

· В алгоритме должен быть только один блок начала и один блок окончания.

При проектировании визуальных алгоритмов используют специальные графические элементы, называемые графически блоками, которые представлены на рис. 1.

Результатом алгоритмизации решения задачи является блок-схема алгоритма, состоящая из некоторой последовательности таких графических блоков.

 

Рис.1. Основные блоки визуальных алгоритмов

 

Одним из системных методов разработки алгоритмов является метод структурной алгоритмизации. Этот метод основан на визуальном представлении алгоритма в виде последовательности управляющих структурных фрагментов. Выделяют три базовые управляющие процессом обработки информации структуры: композицию,

альтернативу и итерацию.С помощью этих структур можно описать любые процессы обработки информации.

Композиция (следование) - это линейная управляющая конструкция, не содержащая альтернативу и итерацию. Она предназначена для описания единственного процесса обработки информации.

Альтернатива - это нелинейная управляющая конструкция, не содержащая итерацию. Она предназначена для описания различных процессов обработки информации, выбор которых зависит от значений входных данных.

Итерация - это циклическая управляющая структура, которая содержит композицию и ветвление. Она предназначена для организации повторяющихся процессов обработки последовательности значений данных.

В соответствии с наличием в алгоритмах управляющих структур композиции, альтернативы и итерации алгоритмы классифицируют на: линейные, разветвленные и циклические алгоритмы.

Линейные алгоритмы не содержат блока условия. Они предназначены для представления линейных процессов. Такие алгоритмы применяют для описания обобщенного решения задачи в виде последовательности модулей. Пример линейного алгоритма приведен на рисунке 2.

 

 

Рис. 2. Пример линейного визуального алгоритма

 

 

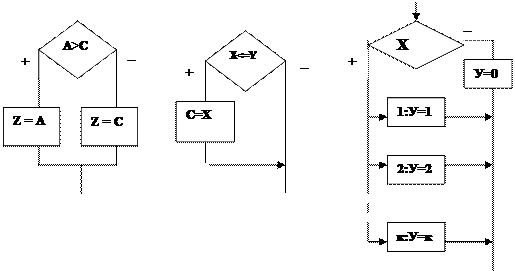
Разветвленные алгоритмы в своем составе содержат блок условия и различные конструкции ветвления. Ветвление - это структура, обеспечивающая выбор между альтернативами.

 

 

 

а) ветвление б)неполное ветвление в) многоальтернативный выбор

 

Рис. 3. Структуры ветвления

 

 

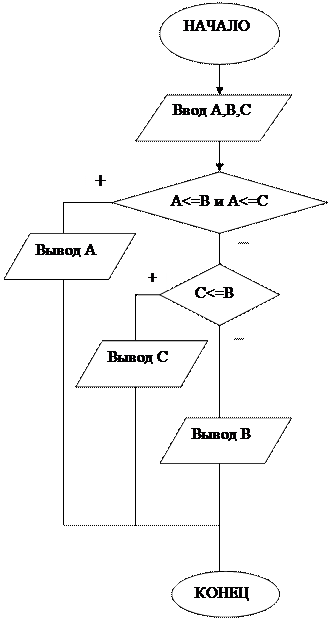
Каждая управляющая структура ветвления имеет один вход и один выход. Ветвления содержат блок условия, в котором записывают логические условия, такие как А >С, X<= Y. В зависимости от значений переменных А,С в управляющей структуре ветвления на рис. 3 а) условие А >С принимает значение "истина" или "ложь" и процесс вычислений включает блок действия Z=A или Z=C. Аналогично происходит и в управляющей структуре неполного ветвления (рис. 3 б)). Только в этом случае, если условие X<= Y истинно, то выполняется действие С=Х, в противном случае никаких действий не выполняется.

В управляющей структуре многоальтернативный выбор в блоке условия записывается переменная, в данном случае Х, которая может принимать различные значения (рис. 3 в)). Если значение пременной Х совпадет с одним из значений в блоке действия, то выполняется действия, записанные в этом блоке. Например, если Х=1, то выполнится действие У=1. Если значение Х не совпало ни с одним из значений, указанных в блоках справа, то выполняется действие в блоке слева, которого также как и в неполном ветвлении может и не быть.

Пример 1. Составить алгоритм нахождения минимального значения из 3-х чисел. Решение. Для определения минимального значения будем использовать проверку пары значений. Визуальные разветвленные алгоритмы приведены на рис.5,6,7. Эти алгоритмы использует для обозначения чисел переменные значения А,В,С и вложенные структуры ветвления.

 

Рис. 4. Поиск минимального значения из трех чисел A,B,C при помощи двойного сравнения.

 

 

Рис. 5.Поиск минимального числа из трёх А,В,С.

Метод последовательного сравнения.

 

 

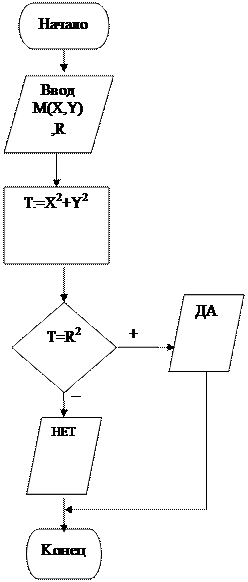
Пример 2. Составить алгоритм определения находится ли точка М с координатами Х,У на окружности радиуса R.

Решение. Визуальный алгоритм приведен на рис. 8.Для решения в нем используется математическая модель в виде формулы окружности R² = X²+Y².

 

Рис. 6.Поиск минимального Рис. 7. Определить находит-

числа из трёх А,В,С. Метод ся ли точка М с координа-

сравнения с промежуточной ми Х,У на окружности

переменной М. радиуса R.

 

 

Пример 4. Составить алгоритм определения корней уравнения (X²+B*X+C=0).

Решение. При составления этого алгоритма надо рассмотреть случаи, когда уравнение не имеет корней и когда имеется только один корень.Обозначим корни уравнения через переменные Х1,Х2. D - промежуточная переменная для вычисления дискриминанта. Алгоритм вычисления корней уравнения заданного вида приведен на рис. 9.

 

 

 

 

Рис.8. Алгоритм вычисления корней уравнения X²+B*X+C=0

 

Задания №1.

Составить визуальные разветвленные алгоритмы для следующих задач (вариант выбирается по последней цифре учебного шифра).

 

1.Для двух чисел Х,У определить, являются ли они корнями уравнения А*Р^4+D*P^2+C=0

2.Если среди трех чисел А,В,С имеется хотя бы одно четное вычислить максимальное, иначе - минимальное

3.Ввести положительное А>=1. Найти наибольшее из выражений вида 1\А и SIN(A).

4.Ввести два числа. Меньшее заменить полусуммой, а большее - удвоенным произведением.

5.Ввести три числа А,В,С. Удвоить каждое из них, если А>=В>=С, иначе поменять значения А и В.

6.Определить является ли точка с координатами X,Y точкой пересечения диагоналей квадрата со стороной R,одна вершина которого расположена в начале координат.

7.Определить значения функции в зависимости от значения аргумента

а*х², если х > 10

у= 1/х, если –10 £ х £ 10

Sin(х), если х < 10

8.Ввести положительное А>=10. Найти наибольшее из выражений вида А/(2A) и COS(A).

9.Ввести два числа. Меньшее заменить произведением, а большее – остатком от деления первого числа на второе.

0.Ввести три числа А,В,С. Удвоить каждое из них, если А=В+С, иначе поменять значения А и В.

 

 

ЦИКЛИЧЕСКИЕ АЛГОРИТМЫ

 

Циклические алгоритмы являются наиболее распространенным видом алгоритмов, в них предусматривается повторное выполнение определенного набора действий при выполнении некоторого условия. Такое повторное выполнение часто называют циклом.

Существуют два основных видов циклических алгоритмов: циклические алгоритмы с предусловием, циклические алгоритмы с постусловием. Они отличаются друг от друга местоположением условия выхода их цикла.

Цикл с предусловием начинается с проверки условия выхода из цикла. Это логическое выражение, например I<=6. Если оно истинно, то выполняются те действия, которые должны повторяться. В противном случае, если логическое выражение I<=6 ложно, то этот цикл прекращает свои действия.

Цикл с постусловием функционирует иначе. Сначала выполняется один раз те действия, которые подлежат повторению, затем проверяется логическое выражение, определяющее условие выхода из цикла, например, I>6.Проверка его осуществляется тоже по-другому. Если условие выхода истинно, то цикл

 

 

а) Цикл с постусловием б) Цикл с предусловием

 

Рис. 9. Виды циклических алгоритмов

 

 

с постусловием прекращает свою работу, в противном случае - происходит повторение действий, указанных в цикле. Повторяющиеся действия в цикле

называются "телом цикла". Разновидности циклов приведены на рис. 9а),б).

Классическим примером циклического алгоритма служит алгоритм для вычисления степени числа Y=Xⁿ. Этот алгоритм может быть реализован на основе операции умножения. Табличное представление такого алгоритма, отражающего зависимость У от Х при изменении показателя степени n от 1 до 3, представлено в табл.1. В этой таблице показанны также реккурентные соотношения между У и Х, определяющие как на каждом шаге зависит значение У от значения Х и от значения У, вычисленного на предыдущем шаге.     Таблица 1.Реккурентные соотношения при вычислении Y=Xⁿ
n	Y	Реккурентные соотношения
	Y[1]=X	Y=X
	Y[2]=X*X или Y[2]=Y[1]*X	Y=X*X или Y=Y*X
	Y[3]=X*X*X или Y[3]=Y[2]*X	Y=X*X*X или Y=Y*X
Рис.11. Алгоритм вычисления суммы ряда S=x+x^2+x^3+…+x^n     Пример 5. Пусть требуется составить алгоритм вычисления суммы ряда S=x+x^2+x^3+…+x^n. Решение. Исходные данные для алгоритма это переменные x и n. На каждом шаге будем вычислять очередной член суммы Y и прибавлять его к предыдущему значению суммы S.Для этого используем реккурентную формулу вычисления степени Х (см. таблицу 3) Y=Y*Х, тогда сумма ряда на каждом шаге итерации будет вычисляться по формуле S=S+Y. Количество итераций K изменяется от 1 до n и равно количеству членов ряда. Начальное значение суммы ряда S равно 0. На рис. 11 представлен циклический алгоритм с предусловием для вычисления заданной суммы ряда.   Пример 6. Требуется составить алгоритм получения на отрезке [-15,15] множества значений функции Y= SIN(X) в виде таблицы значений (X,Y) при изменении аргумента Х по формуле X[k]=X[k-1]+h, где h=1,5. Решение. Такие задачи относят к задачам табулирования функций. Из условия задачи определяем, что начальное значение отрезка табулирования X= -15, конечное значение - X=15. Процесс получения множества пар Х,Y) является итерационным, значит проектируемый алгоритм будет циклическим. Условие выхода из цикла Х>15. На рис. 13 представлен циклический алгоритм с предусловием вычисления табличного значения функции Y= SIN(X) на отрезке -15<X<15 при изменении Х на каждом шаге итерации на величину 1,5. Результатом выполнения алгоритма является циклический вывод множеств пар (Y,X).

Рис. 13. Циклический алгоритм табулирования функции Y =sin (X)

 

 

Задания №2:

Составить визуальные циклические алгоритмы для следующих задач (номер варианта определяется по последней цифре учебного шифра).

1. Вычислить число в факториале Y=X!

2. Вычислить сумму ряда, общий член которого задан формулой An=(x*n)/n!.

3. При табулировании функции y=cos(x+a) на отрезке [1,10] c шагом h=1 определить сумму значений y, больших p.

4. Подсчитать количество цифр в целом числе Х.

5. Вычислить сумму значений функции у=x^2 на отрезке [1,5] c шагом 1.

6. Найти минимальное значение функции Y=Sin(X)*X, на отрезке [C,D] с шагом 0.001. Реализовать цикл с постусловием.

7. Составить алгоритм табулирования функции y=sin(x) на отрезке [1,5] с шагом h=0,5. Вывести предпоследнее положительное значение функции.

8. Определить постановку задачи и составить визуальный алгоритм для этой задачи, если табличное представление ее решения изображено ниже:

 

Условие N>0	S	N
125>0 да	0+5=5
12>0 да	5+2=7
1>0 да	7+1=8
0>0 нет

 

9. Составить визуальную и табличную формы алгоритма по его текстовому представлению, а также определить конечное значение S.

 

А) I=0; S=0; В) I=1; S=0;

ПОКА I<3 ПОКА I >1

I=I+3 S=S+1/I

S=S+I*I I=I-1

ВЫВОД S ВЫВОД S

 

0. Составить визуальную и текстовую форму представления алгоритма, заданного в табличной форме.

 

I	J	S
		0+1+2=3
		3+1+3=7
		7+2+2=11
		11+2+3=16

 

Задание №3

Составить визуальные циклические алгоритмы для следующих задач обработки последовательности значений (номер варианта определяется по последней цифре учебного шифра).

 

1. В последовательности чисел подсчитать произведение чисел, кратных 3.

2. В последовательности чисел сравнить,что больше сумма положительных или произведение отрицательных.

3. В последовательности чисел определить предпоследнее отрицательное число.(При решении введите дополнительную переменную для хранения предпоследнего отрицательного числа).

4. В последовательности целых положительных чисел определить

максимальное число (Рекомендуем реализовать такой алгоритм:

Вводим Х

mах=Х

Цикл с постусловием

а. Если элемент Х > max

то max:=Х (значение этого элемента);

б. Вводим новый элемент последовательности Х.

Условие выхода из цикла Х=0)

5. В последовательности целых чисел определить третье положительное число и подсчитать количество цифр в нем.

6. В последовательности чисел подсчитать произведение чисел, кратных 8.

7. В последовательности чисел сравнить,что больше модуль суммы отрицательных или сумма положительных значений.

8. В последовательности чисел определить предпоследнее четное число.(При решении введите дополнительную переменную для хранения предпоследнего четного числа).

9. В последовательности чисел определить предпоследнее нечетное число. (При решении введите дополнительную переменную для хранения предпоследнего нечетного числа)

0. В последовательности чисел подсчитать произведение чисел, кратных 10.

 

 

Задание на контрольную работу часть2

 

Задача 1.1

(вариант выбирается по последней цифре учебного шифра)

Средствами табличного процессора EXEL вычислить значение заданной функции и построить её график. Исходные данные приведены в таблице 1

 

 

Таблица.1

Варианты заданий к задаче 1.1

 

Последняя цифра шифра	Функция	Отрезок (Хн, Хк)	Шаг DХ
		-5;6	1,0
		-6;7	1,0
		-5;4	1,0
		-4;5	1,0
		-3;8	1,0
		-6;7	1,0
		-8;6	1,0
		-6;8	1,0
		-6;6	1,0
		-6;6	1,0

 

Задача 1.2

(вариант выбирается по последней цифре шифра)

 

Средствами табличного процессора EXCEL выполнить следующие операции:

- сформировать в электронной таблице циклический алгоритм вычисления функций Y, Z, F1, F2 для заданных значений Х₁=Х_нач, Х₂=Х_кон, Х₃=ΔХ;

- вычислить значения указанных функций;

- Построить графики зависимостей Y, Z =F(X)

Исходные данные и расчетные формулы приведены в таблице 2

 

 

Таблица 2

Варианты к задаче 1.2

 

Послед. цифра шифра	Х1	Х2	Х3	Y	Z	F1	F2
	1.2	2.1	0.19	arctg x
	1.3	2.2	0.18
	1.4	2.3	0.17	ln x
	1.5	2.4	0.16	lg x
	1.6	2.5	0.15	cos x
	1.7	2.6	0.14	sin x
	1.8	2.7	0.13	tg x/10
	1.9	2.8	0.12
	2.0	2.9	0.11
	1.1	2.0	0.20				arctg z

 

 

Задача 1.3

(Выполняется без вариантов)

 

Средствами табличного процессора EXCEL выполнить следующие операции:

- сформировать на экране произвольный массив (матрицу) чисел размером 5х5 (пять строк, пять столбцов)

- вычислить сведущие параметры сформированной матрицы:

- максимальные и минимальные элементы по строкам и столбцам;

- суммы элементов по строкам и столбцам;

- общую сумму элементов матрицы;

- определитель матрицы;

- обратную матрицу;

- сделать проверку получения обратной матрицы (перемножить исходную и обратную матрицы для получения единичной матрицы)

 

Задача 1.4

(вариант выбирается по последней цифре учебного шифра)

 

Средствами табличного процессора EXCEL выполнить следующие операции:

- сформировать на экране заданную систему трех линейных алгебраических уравнений по следующей схеме:

 

A₁₁X₁ + A₁₂X₂ + A₁₃X₃ = B₁

A₂₁X₁ + A₂₂X₂ + A₂₃X₃ = B₂

A₃₁X₁ + A₃₂X₂ + A₃₃X₃ = B₃

 

- вычислить значения корней сформированной системы уравнений двумя методами: обратной матрицы и по формулам Крамера;

 

Исходные данные для решения задачи 1.4 приведены в таблице 3.

 

 

Таблица 3

Варианты к задаче 1.4

 

Последняя цифра шифра	А - коэффициенты системы уравнений	В - свободные члены
А11-А31	А12-А32	А13-А33	В1-В3
	2.58 1.32 2.09	2.98 1.55 2.25	3.13 1.58 2.34	-6.66 -3.58 -5.01
	2.18 2.17 3.15	2.44 2.31 3.22	2.49 2.49 3.17	-4.34 -3.51 -5.27
	1.54 3.65 2.45	1.70 3.73 2.43	1.62 3.59 2.25	-1.97 -3.74 -2.26
	1.53 2.35 3.83	1.61 2.31 3.72	1.43 2.07 3.45	-5.13 -3.69 -5.98
	2.36 2.51 2.59	2.37 2.40 2.41	2.13 2.10 2.06	1.48 1.92 2.16
	3.43 4.17 4.30	3.38 4.00 4.10	3.09 3.55 3.67	5.32 6.93 7.29
	3.88 3.00 2.67	3.78 2.79 2.37	3.45 2.39 1.96	10.41 8.36 7.62
	3.40 2.64 4.64	3.26 2.39 4.32	2.90 1.96 3.85	13.05 10.30 17.86
	2.53 3.95 2.78	2.36 4.11 2.43	1.93 3.66 1.56	12.66 21.97 13.93
	1.84 2.32 1.83	2.25 2.60 2.06	2.53 2.82 2.24	-6.09 -6.98 -5.52

 

Контрольной работы №1

Задача 1.1

Выполнение задачи 1.1 осуществляется с использованием табличного процессора EXCEL при этом необходимо выполнить следующие операции:

- запуск EXCEL;

- формирование электронной таблицы циклического вычисления заданной математической функцией и с использованием операции копирования;

- сохранение созданной электронной таблицы;

Для выполнения операции копирования необходимо выделить ячейку, содержащую результат вычисления по выбранной формуле, поставить курсор на специальный указатель (в нижнем правом углу ячейки и принажатой левой кнопки "мыши" протащить указатель по всем необходимым ячейкам. При этом выделенная область будет заключена в рамку. При отпускании левой кнопки "мыши" во всех выделенных ячейках появятся соответствующие результаты вычислений.

 

Задача 1.2

Выполнение задачи 1.2 осуществляется с использованием табличного процессора при этом необходимо выполнить следующие операции: запуск EXCEL, создание электронной таблицы с использованием стандартных математических функций, сохранение электронной таблицы.

При создании электронной таблицы прежде всего необходимо ввести заголовок решаемой задачи. Для этого необходимо курсор подвести к начальной ячейке заголовка и щелкнуть левой кнопкой манипулятора "мышь". Выбранная ячейка станет активной и готовой для ввода текста заголовка. После этого необходимо ввести текст заголовка прописными (заглавными) буквами и нажать клавишу "ENTER". Например, для задачи 1.2 заголовок может выглядеть следующим образом:

 

Задача 1.2 (циклическое вычисление функций: Y, Z, F1, F2) Исходные данные: Хнач = 1.1 Хкон = 2.0 ΔХ = 0.2

 

После ввода заголовка необходимо ввести в электронную таблицу расчетные формулы. Для этого последовательно активизируются необходимые ячейки и перед первым символом вводимой формулы набирается знак равенства ("=").

В табличном процессоре EXCEL существует большая библиотека стандартных математических функций, которые могут использоваться как отдельно, так и в составе более сложных формул.

Стандартные математические функции табличного процессора EXCEL, которые могут потребоваться при решении задачи 1.2 приведены в таблице 4.

 

Таблица 4.

 

Стандартные математические

Задача 1.3

Выполнение задачи 1.3 также осуществляется с использованием табличного процессора EXCEL. При этом необходимо выполнить следующие операции:

- запуск EXCEL;

- создание электронной таблицы с произвольным массивом чисел размером 5х5;

- создание расширенной электронной таблицы с выполнением необходимых матричных операций, заданных в условии задачи 1.3;

- сохранение созданной электронной таблицы;

- вывод электронной таблицы на печать.

Стандартные математические функции, необходимые для решения задачи 1.3 приведены в таблице 5.

Таблица 5.

Задача 1.4

 

Выполнение задачи 1.4 также осуществляется с использованием табличного процессора EXCEL. При этом необходимо выполнить следующие операции:

- запуск EXCEL;

- создание электронной таблицы с заданной системой трех алгебраических уравнений;

- решение системы алгебраических уравнений методами обратной матрицы и по формулам Крамера;

- сохранение полученной электронной таблицы с результатом вычисления корней уравнений;

Стандартные математические функции, необходимые для решения задачи 1.4 приведены в таблице 6.

Таблица 6.

Теоретические сведения.

Понятие «Электронная таблица»

Довольно часто обрабатываемая информация в различных задачах представляется в виде таблиц. Обычная таблица отображает неизменяемую информацию. Электронная таблица, в отличие от обычной таблицы, не только позволяет отображать данные в табличной форме, но и выполнять их обработку. Кроме того, электронная таблица может содержать поясняющий текст, рисунки, диаграммы и др.

Для современных компьютеров разработано большое количество программ, предназначенных для решения задач, в которых данные можно представить в виде таблиц. Наиболее популярной является программа обработки электронных таблиц Microsoft Excel (далее – Excel).

Документом, т.е. объектом обработки Excel является файл с произвольным именем и расширением. XLS. Такой файл в терминах Excel называется рабочей книгой (WorkВook). В каждом файле XLS может размещаться от 1 до 255 электронных таблиц, каждая из которых называется рабочим листом (Sheet).

Электронная таблица Microsoft Excel включает в себя множество ячеек, строку заголовков столбцов и столбец заголовков строк (см. рис. 1.1).

 

	A	B	C	D	E	F	G

 

 

Рис. 1.1. Общий вид электронной таблицы

 

Ячейка (cell) представляет собой основной структурный элемент таблицы, располагающийся на пересечении столбца и строки. Текущая ячейка выделена более темным контуром.

Часть ячеек таблицы может содержать исходную или первичную информацию, а часть - производную. Производная информация является результатом различных арифметических и иных операций, совершаемых над первичными данными.

Номер ячейки (относительный адрес или просто адрес) получается из заголовков столбца и строки, на пересечении которых находится ячейка, например: A1, B3, …. При некоторых операциях копирования, удаления, вставки Excel автоматически изменяет этот адрес в формулах. Иногда это служит источником ошибок. Чтобы отменить автоматическое изменение адреса данной ячейки, ей можно назначить абсолютный адрес. Для этого необходимо поставить перед номером столбца и (или) перед номером строки знак доллара «$». Например, в адресе $А5 не будет меняться номер столбца, в адресе В$7 – номер строки, а в адресе $D$12 – ни тот, ни другой номер.

Чтобы сослаться на диапазон ячеек (например, на группу смежных ячеек в строке), нужно указать через двоеточие адреса начальной и конечной ячеек в диапазоне. Например, обозначение A7:D7 адресует ячейки A, B, C, D в строке 7. Диапазоном можно обозначить и прямоугольный блок ячеек, например, C6:F9. Адреса ячеек можно набирать заглавными или строчными буквами только в латинском алфавите.

Кроме того, в Excel предусмотрен очень удобный способ ссылки на ячейку с помощью присвоения этой ячейке произвольного имени. Чтобы присвоить ячейке имя, необходимо выделить ее и выбрать команду«Вставка|Имя|Присвоить» На экране появится диалоговое окно «Присвоение имени», в котором в поле «Имя» следует набрать произвольное имя и нажать кнопку ОК. Выделенной ячейке будет присвоено имя, которое можно использовать в дальнейшем вместо адреса.

Электронная таблица Excel состоит из 16384 строк (row) и 256 столбцов (column), размещенных в памяти компьютера. Строки пронумерованы целыми числами от 1 до 16384, а столбцы обозначены буквами латинского алфавита А, В,..., Z, АА, АВ,..., IV.

В любую ячейку электронной таблицы можно ввести:

число;

формулу (последовательность символов, которая начинается со знака «=«), например:

=A2+C3*F7

=Sum(A2:F2)

текст (произвольный набор символов).

Ввод любого типа информации должен завершаться нажатием клавиши Enter или выбором новой ячейки с помощью мыши.

Любая последовательность символов, в которую входят цифры, а также знаки «+», «–» (в начале последовательности) или «,» (как разделитель целой и дробной части), считается числом.

После ввода числа Excel сдвигает его к правой границе ячейки, однако его можно выровнять по центру ячейки или сместить к левой границе ячейки с помощью к