
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностные основы теории информации. Понятие энтропии. Энтропия случайной величины. Условная и средняя энтропия. Информация и ее измерение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теория информации как самостоятельная дисциплина возникла в ходе решения следующей задачи: обеспечить надежную и эффективную передачу информации от источника к приемнику при условии, что передаче этой препятствуют помехи. Сама формулировка этой задачи нуждается в ряде уточнений: - «надежную» означает, что в процессе передачи не должно происходить потери информации - приемник полностью, без искажений должен получить информацию, отправленную источником; - «эффективную» означает, что передача должна осуществляться наиболее быстрым способом, поскольку время эксплуатации линии связи - экономический фактор, который требуется минимизировать; - помехи присутствуют в любой реальной линии связи; таким образом, поставленная выше задача имеет четкую практическую направленность. Решение этой задачи ведется по двум направлениям, которые условно можно назвать техническим и математическим. Технический поиск связан с практической разработкой линий связи, в которых передача может идти с большой скоростью; обеспечением защиты от помех или уменьшения их воздействия; созданием технических устройств, обеспечивающих быструю и надежную связь. Однако в основе этих разработок лежат некоторые общие законы и принципы, применимые не к какой-то конкретной линии передачи информации, а к любым (во всяком случае, многим) видам связи. Они определяют способы кодирования информации (в том числе такие, которые позволяют обнаружить и исправить ошибку передачи); условия надежной передачи информации; наконец, что очень важно, вводятся величины, позволяющие количественно описывать информационные процессы. Именно эти методы и составляют содержательную основу теории информации. Теория информации является математической теорией с высокой степенью общности. Она основывается на теории случайных событий, для описания которых применяются понятия вероятность и энтропия. В рамках самой теории вводится понятие информация и устанавливается ее мера - бит. Строится теория информации подобно другим теориям в математике: сначала аксиоматически определяются исходные понятия, а затем из них путем рассуждений доказывается справедливость новых положений или теорем - именно таким путем шел основоположник данной теории Клод Шеннон. В дальнейшем изложении большее внимание будет уделено смыслу и значению теорем, нежели их доказательству. Отдельно следует остановиться на практической применимости положений и следствий, выводимых в теории. Примеры использования теории информации можно найти в информатике, технике, психологии, биологии, физике, педагогике, лингвистике и т.д. Однако, как и любая иная математическая теория, теория информации применима для решения конкретных задач практики в той мере, в какой описываемые материальные системы или процессы удовлетворяют исходным положениям теории. Неприменимость ее в остальных случаях ни в коем случае нельзя считать недостатком теории. Речь, в частности, идет о том, что сам исходный термин -информация - используется не только в данной теории; однако, если в других дисциплинах (например, философии) ему придается иной смысл, то нельзя требовать, чтобы теория информации была в них применима. Точно также механика Ньютона является теорией, описывающей движение, но не во всем многообразии значений этого термина, а лишь перемещение тел в пространстве с течением времени; другие виды движения - развитие растения, эволюция Вселенной, изменения в общественном устройстве и т.п. - законами Ньютона, безусловно, не описываются, но это не уменьшает значимости последних. Математическое понятие информации связано с возможностью ее количественного измерения. При этом в теории информации обосновывается энтропийный подход, когда количество информации в сообщении определяется тем, насколько уменьшается неопределенность исхода случайного события (например, появления конкретной буквы в некоторой последовательности символов) после получения сообщения. Сообщение несет полную информацию о событии, если оно целиком снимает исходную неопределенность. В технических приложениях используется иной способ оценки количества информации, основанный на простом подсчете числа знаков в сообщении - такой подход получил название объемного. В общем случае эти две меры количества информации не совпадают, в частности, в теории информации показывается, что энтропийная мера не превышает числа двоичных символов (бит) в сообщении. Одинаковым же в обоих подходах оказывается то, что количественная мера информации не привязывается к ее семантической (т.е. смысловой) основе. С бытовой точки зрения информация, лишенная смысла, лишена и какой-либо ценности для получателя. Однако устройство, предназначенное для передачи или хранения информации, оценить смысл передаваемого (или сохраняемого) не может (да и не должно!) - в этом случае главной оказывается задача надежной передачи и хранения информации независимо от ее семантической основы. Едва ли кого-либо устроила бы ситуация, если бы почтальон стал оценивать содержание писем и в зависимости от своего понимания их значимости и ценности решать, какие из них доставлять, а какие нет. Почтальон, будучи средством связи, обязан доставить пакет адресату, даже если в нем чистый лист бумаги. При этом важными (существенными) для передачи и хранения оказываются количественные характеристики информации и способы их оценки - именно их теория информации и устанавливает. Таким образом, оказывается, что теория информации применима для решения лишь тех практических задач, в которых допустимо игнорирование смысловой (содержательной) стороны информации. 26. Закона распределения случайной величины. Понятие и методика определения статистической функции и статистической плотности распределения. Виды статистических оценок и предъявляемые к ним требования. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Распределением признака называется закономерность встречаемости разных его значений (Плохинский Н.А., 1970, с. 12). В психологических исследованиях чаще всего ссылаются на нормальное распределение. Нормальное распределение характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения, близкие к средней величине – достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречалось в естественнонаучных исследованиях и казалось "нормой" всякого массового случайного проявления признаков. Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции (Плохинский Н.А., 1970, с.17). График нормального распределения представляет собой привычную глазу психолога-исследователя так называемую колоколообразную кривую. Другие виды распределений называют отклоняющимися от нормального (ненормальными). Параметры распределения и их оценки. Параметры распределения - это его числовые характеристики, указывающие, где "в среднем" располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Наиболее практически важными параметрами являются меры центральной тенденции и меры изменчивости. В реальных исследованиях мы оперируем не параметрами, а их приближенными значениями, так называемыми оценками параметров. Это объясняется ограниченностью обследованных выборок. Чем больше выборка, тем ближе может быть оценка параметра к его истинному значению. В дальнейшем, говоря о параметрах, мы будем иметь в виду их оценки. Меры центральной тенденции являются наиболее часто используемыми мерами при описании совокупностей данных. Наиболее распространенными среди них являются: среднее арифметическое( 27. Статистическая проверка гипотез: сущность методов, основные понятия и определения. Примеры решения задач. Проверка статистических гипотез тесно связана с теорией оценивания параметров. В естествознании, технике экономике для вычисления того или иного случайного факта часто прибегают к высказыванию гипотез, которые можно проверить статистически (то есть, опираясь на результаты наблюдений в случайной выборке). Подстатистическими подразумевают такие гипотезы, которые относятся или к виду, или к отдельным параметрам распределения случайной величины. Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых условиях, имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры деталей, производимых на однотипных, параллельно работающих станках, не различаются. Статистическая гипотеза называется простой, если она однозначно определяет распределение случайной величины Другим примером сложной гипотезы является предположение о том, что непрерывная случайная величина Часто распределение величины Проверяемая гипотеза называется нулевой и обозначается Правило, по которому принимается решение принять или отклонить гипотезу Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность,– достоверными. Этот принцип можно реализовать следующим образом. Перед анализом выборки фиксируется некоторая малая вероятность Основные понятия теории вероятностей: случайные события, величины, характеристики и функции. Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. Случайное событие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом Случайное событие - это закономерное событие созданное генерированием случайных функций с подстановкой в переменные случайных величин. Более простая функция генерирования случайного числа реализована средствами ЭВМ. Случайная величина является одним из основных понятий теории вероятностей. Роль случайной величины, как одного из основных понятий теории вероятностей, впервые была чётко осознана П. Л. Чебышевым, который обосновал общепринятую на сегодня точку зрения на это понятие (1867). Понимание случайной величины как частного случая общего понятия функции, пришло значительно позднее, в первой трети 20 века. Впервые полное формализованное представление основ теории вероятностей на базе теории меры было разработано А. Н. Колмогоровым (1933), после которого стало ясным, что случайная величина представляет собой измеримую, определенную на вероятностном пространстве. В учебной литературе эта точка зрения впервые последовательно проведена У. Феллером (см. предисловие к, где изложение строится на основе понятия пространства элементарных событий и подчеркивается, что лишь в этом случае представление случайной величины становится содержательным). Случайные величины используются для математического представления таких сторон объектов, систем и событий, количественную характеристику которых до проведения опыта по их измерению, однозначно определить принципиально невозможно. Примером таких систем могут служить микроскопические объекты, состояние которых описывается квантовой механикой. Случайными величинами описываются события передачи наследственных признаков от родительских организмов к их потомкам (см. Законы Менделя). Следует также отметить, что существует ряд задач математического анализа и теории чисел для которых участвующие в их формулировках функции целесообразно рассматривать как случайные величины, определенные на подходящих вероятностных пространствах.
|
||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.199.240 (0.01 с.) |

 ), медиана(Me или Md) и мода(Mo).
), медиана(Me или Md) и мода(Mo). , в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина
, в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина  , то это сложная гипотеза.
, то это сложная гипотеза. принимает значение из интервала
принимает значение из интервала  , в этом случае распределение случайной величины
, в этом случае распределение случайной величины  . Наряду с гипотезой
. Наряду с гипотезой 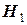 . Например, если проверяется гипотеза о равенстве параметра
. Например, если проверяется гипотеза о равенстве параметра  некоторому заданному значению
некоторому заданному значению  , то есть
, то есть  , то в качестве альтернативной гипотезы можно рассматривать одну из следующих гипотез:
, то в качестве альтернативной гипотезы можно рассматривать одну из следующих гипотез:  , где
, где  – заданное значение, причём
– заданное значение, причём  . Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
. Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.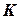 . Так как решение принимается на основе выборки наблюдений случайной величины
. Так как решение принимается на основе выборки наблюдений случайной величины 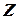 критерия
критерия  , называемаяуровнем значимости. Пусть
, называемаяуровнем значимости. Пусть 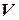 – множество значений статистики
– множество значений статистики  – такое подмножество, что при условии истинности гипотезы
– такое подмножество, что при условии истинности гипотезы  равна
равна  .
. . Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом
. Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом  .
.


