
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая модель межотраслевого баланса. Балансовый метод. Распределение продукции. Структура стоимости: перенесенная на продукт стоимость, вновь созданная стоимость.Содержание книги
Поиск на нашем сайте
Межотраслевой баланс (МОБ) – это определение взаимосвязей между выпуском продукции в одной отрасли и затратами и потреблением товаров всех отраслей, задействованных в производстве этой продукции. Например, для добычи угля необходимы стальные инструменты; в то же время для выплавки стали нужен уголь. Задача межотраслевого баланса заключается в том, чтобы найти такое соотношение угля и стали, при котором экономический результат будет максимальным. В более широком понимании можно говорить, что по результатам: построенной модели можно определять эффективность производства вообще, находить оптимальные методы ценообразования и выявлять наиболее значимые факторы экономического роста. Кроме того, этот метод позволяет заниматься прогнозированием. Балансы бывают отчетные и плановые. Отчетные фиксируют сложившиеся пропорции, а плановые отражают некоторое желательное состояние и получаются в результате расчета по моделям (о которых и пойдет речь в этой главе). В зависимости от того, в каких единицах измеряются межотраслевые потоки, различают балансы натуральные и стоимостные (Далее мы будем иметь в виду стоимостные балансы). Балансовая модель – это система дифференцированных уравнений (и не всегда линейных), которые отображают условия равновесия между произведенной в отрасЛи совокупной продукцией и потребностью в ней. Модели экономических систем: чаще всего представляются: в виде таблицы. В ней совокупный продукт разделяется на 2 части: - внутренний (промежуточный) - конечный. Народное хозяйство рассматривается как система из п чистых отраслей, каждая из которых выступает в роли производящей и потребляющей. Межотраслевой баланс разделен на четыре части. Каждая часть (они обозначены цифрами 1-4) имеет свое экономическое содержание. В первой отображаются межотраслевые материальные связи. Каждая отрасль представлена в МОБ дважды: как производящая и как потребляющая. Отрасли как производителю соответствует строка таблицы, отрасли как потребителю соответствует столбец. На пересечении i-й строки и j-го столбца находится величина xij – количество продукции i-й отрасли (в денежном выражении), израсходованной на производственные нужды j-й отрасли. Таким образом, первый раздел характеризует межотраслевые потоки сырья, материалов, энергии и т. д., обусловленные производственной деятельностью отраслей. Обозначение х23, например, следует трактовать так: стоимость средств производства, выпущенных в отрасли 2 и потребленных в отрасли 3 (материальные затраты). Сумма всех элементов первой части представляет собой годовой фонд возмещения материальных затрат. Вторая часть представляет собой совокупность конечной продукции всех производственных отраслей и состоит из двух столбцов. Конечным называется продукт, который выходит за рамки производственной сферы в область конечного потребления и накопления. Развернутая схема баланса иллюстрирует направления использования такого товара: общественное и личное потребление, накопление, возмещение и экспорт. Столбец Y - это конечная продукция отраслей. Конечная продукция включает в себя непроизводственное потребление (личное и общественное), возмещение выбытия основных фондов и накопление. Столбец X содержит величины валового производства отраслей. Третяя часть описывает национальный доход. Он представляет собой сумму чистой продукции (оплата труда и чистый доход отраслей) и фонда, возмещения. Третий раздел представлен двумя нижними строками. Строка X содержит те же самые величины, что и соответствующий столбец второго раздела. Строка V содержит величины условно-чистой продукции отраслей. Условно-чистая продукция включает в себя амортизационные отчисления и вновь созданную стоимость (заработную плату и прибыль). А в четвертой отображена информация о конечном распределении. Она находится на пересечении столбцов второй и строк третьей части. Эта информация необходима для понимания формирования системы доходов и расходов населения страны, источников финансирования, затрат непроизводственной сферы и т. д. 22. Виды дифференциальных уравнений. Обыкновенные дифференциальные уравнения. Уравнения в полных дифференциалах. Второй закон Ньютона. Простейшие дифференциальные уравнения. Алгоритмы решения и примеры. Дифференциальное уравнение первого порядка имеет вид
Если это уравнение разрешено относительно Для дифференциального уравнения существует несколько видов решений: общее решение, частное решение и особое решение. Общим решением дифференциального уравнения первого порядка называется функция Частным решением дифференциального уравнения первого порядка называется всякое решение Задача Коши - задача нахождения частного решения дифференциального уравнения при заданном начальном условии: Обыкновенные дифференциальные уравнения - это уравнения вида F (t, x, x ', x '',..., x (n)) = 0, где x = x (t) - неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени t, штрих означает дифференцирование по t. Число n называется порядком дифференциального уравнения. Решением (или решением) дифференциального уравнения называется функция, дифференцируется n раз, и удовлетворяет уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одной из развязок нужно наложить на нее дополнительные условия: например, требовать, чтобы решения принимал в определенной точке определенное значение. Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для ОДУ, методы розьязання простых ОДУ, качественное исследование решений ОДУ без нахождения их явного вида. Уравнение P(x; y)dx + Q(x; y)dy = 0 называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции u(x; y), что имеет место при выполнении условия Если левая часть дифференциального уравнения представить в виде полного дифференциала, то получим
В итоге общее решение дифференциального уравнения в полных дифференциалах имеет вид
Дифференциальные уравнения в частных производных. Классификация. Решение дифференциальных уравнений в частных производных. Примеры. Дифференциальные уравнения в частных производных - это уравнения, содержащие неизвестные функции от нескольких переменных и их частных производных. Общий вид таких уравнений можно представить в виде:
где
ОДУ первого порядка называется уравнение F(x,y,y’)=0 F – известная функция трех переменных; x – независимая переменная на интервале интегрирования[a,b]; y – неизвестная функция; y’ – ее производная. Функция y(x) является решением дифференциального уравнения, если она при всех xÎ[a,b] удовлетворяет уравнению F(x,y(x),y’(x))=0 График решения y(x) называется интегральной кривой дифференциального уравнения. Если не заданы начальные условия, таких решений y(x) будет множество. При известных начальных условиях y(x0)= y0 решение y(x) будет единственным. 24. Основные (исходные) понятия математической статистики: результат наблюдения (испытания), генеральная совокупность, выборка из генеральной совокупности. Математическая статистика – это раздел математики, изучающий приближенные методы сбора и анализа данных по результатам эксперимента для выявления существующих закономерностей, т.е. отыскания законов распределения случайных величин и их числовых характеристик. В математической статистике принято выделять два основных направления исследований: - Оценка параметров генеральной совокупности. - Проверка статистических гипотез (некоторых априорных предположений). Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения. Генеральной совокупностью является набор всех мыслимых статистических данных при наблюдениях случайной величины. ХГ = {х1, х2, х3, …, хN, } = { хi; i=1,N } Наблюдаемая случайная величина Х называется признаком или фактором выборки. Генеральная совокупность – есть статистический аналог случайной величины, ее объем N обычно велик, поэтому из нее выбирается часть данных, называемая выборочной совокупностью или просто выборкой. ХВ = {х1, х2, х3, …, хn, } = { хi; i=1,n } ХВ Ì ХГ, n £ N Выборка – это совокупность случайно отобранных наблюдений (объектов) из генеральной совокупности для непосредственного изучения. Количество объектов в выборке называется объемом выборки и обозначается n. Обычно выборка составляет 5%-10% от генеральной совокупности. Использование выборки для построения закономерностей, которым подчинена наблюдаемая случайная величина, позволяет избежать ее сплошного (массового) наблюдения, что часто бывает ресурсоемким процессом, а то и просто невозможным. Например, популяция представляет собой множество индивидуумов. Изучение целой популяции трудоемко и дорого, поэтому собирают данные по выборке индивидуумов, которых считают представителями этой популяции, позволяющими сделать вывод относительно этой популяции. Однако, выборка обязательно должна удовлетворять условию репрезентативности, т.е. давать обоснованное представление о генеральной совокупности. Как сформировать репрезентативную (представительную) выборку? В идеале стремятся получить случайную (рандомизированную) выборку. Для этого составляют список всех индивидуумов в популяции и случайно их отбирают. Но иной раз затраты при составлении списка могут оказаться недопустимыми и тогда берут приемлемую выборку, например, одну клинику, больницу и исследуют всех пациентов в этой клинике с данным заболеванием.
|
||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.168 (0.011 с.) |

 (8.2)
(8.2) , то это уравнение имеет вид:
, то это уравнение имеет вид:  или
или 
 зависящая от
зависящая от  и от одной произвольной постоянной, и обращающая это уравнение в тождество.
и от одной произвольной постоянной, и обращающая это уравнение в тождество. , полученное из общего решения при фиксированном значении
, полученное из общего решения при фиксированном значении  .
. при
при 
 . (6)
. (6) ,
, 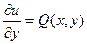 . Интегрируем первое уравнение:
. Интегрируем первое уравнение:  . Применяя второе уравнения, получим уравнение для неизвестной j(y):
. Применяя второе уравнения, получим уравнение для неизвестной j(y):  , откуда можно найти j(y):
, откуда можно найти j(y): .
. .
.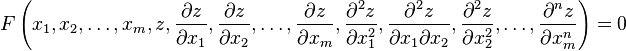 ,
,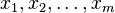 - независимые переменные, а
- независимые переменные, а 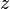 - функция этих переменных.
- функция этих переменных.


