Применение и виды имитационного моделирования.

В настоящее время при разработке сложных систем особенно широкое применение находят методы и средства математического моделирования, которые по сравнению с методами натурного и полунатурного моделирования обладают явными преимуществами в плане ресурсных и временных затрат. Сущность методологической концепции математического моделирования заключается в создании математической модели ИУС и реализации ее на ЭВМ.

Поскольку имитационное моделирование есть разновидность аналогового моделирования тем не менее в отличии от других видов математического моделирования оно имеет определённую специфику, заключающуюся в том, что взаимодействующие вычислительные процессы должны быть аналогичны исследуемым процессам с точностью до масштабов времени и пространства.

Метод математического имитационного моделирования позволяет осуществлять численное моделирование поведения подсистем ИУС и их взаимодействия с учетом возмущений различной природы в течение заданного или формируемого периода времени и не накладывает ограничения на сложность ИУС и может быть принят за основу как инструмент исследований. Процесс имитации на ЭВМ следует понимать и конст­руирование модели, и её испытание, и применение с целью изучения происходящих процессов и предсказания результатов.

Имитационное моделирование (ИМ), осуществляющееся посредством процессов-аналогов набором алгоритмов, реализуемых на не­котором языке моделирования с применением набора математических инструментальных и программных средств, позволяет выполнить целенаправленное исследование реальной сложной системы в режиме «имитации» с целью оптимизации её структуры и функциональных параметров. Тем самым имитационная модель - это специальный программный комплекс, имитирующий функционирование ИУС. При построении ИМИУС надо исходить прежде всего из возможности вычисления функционала, имитирующего различные реальные ситуации, задаваемые на множестве возможных реализаций процесса функционирования ИУС в реальных условиях с некоторым показателем эффективности.

9. Алгебра логики, основные определения, аксиомы, логические операции и их свойства.

Алгебра логики (Булева логика, двоичная логика, двоичная алгебра) - раздел математической логики, изучающий систему логических операций над высказываниями. То есть, представление логики в виде алгебраической структуры.

Основы алгебры логики были сформулированы британцем Джорджем Булем в 1847 году. Позже ее развивали Чарльз Пирс, Генри Шеффер, П. С. Порецкий, Бертран Рассел, Давид Гильберт и др.

С тех пор эта система применяется для решения широкого спектра проблем математической логики и теории множеств, и особенно конструирования цифровой электроники (начало использования алгебры логики для синтеза переключательных (релейных) схем было положено в 1938 году работами известного американского ученого Клода Шеннона).

Сначала проблематика алгебры логики пересекалась с проблематикой алгебры множеств (теоретико-множественные операции).

Однако с окончанием формирования теории множеств (70-е годы 19 в.), которая включила в себя алгебру множеств, и дальнейшим развитием математической логики, предмет алгебры логики значительно изменился.

Современная алгебра логики рассматривает операции над высказываниями, как булеву функцию и изучает их отношении такие вопросы, как:

- таблицы истинности;

- функциональная полнота;

- замкнутые классы;

Базовыми элементами алгебры логики является высказывание. Высказывания строятся над множеством {B,,,, 0, 1}, где B - булева множество, над элементами которой определены три математические операции:

отрицание (унарная операция),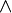

конъюнкция (бинарная),

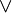дизъюнкция (логическая) (бинарная),

константы - логический ноль 0 и логическая единица 1.