
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы, решение систем линейных уравнений. Интерполирование и приближенные вычисления функций.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В прикладных задачах часто возникает необходимость решать системы линейных уравнений. Система линейных алгебраических уравнений с n неизвестными - это система уравнений вида
Интерполяция – одно из основных направлений обработки данных, которое заключается в нахождении значения таблично заданной функции в тех точках внутри данного интервала, где она не задана. При интерполяции и экстраполяции строится интерполяционная функция L(x), приближённо заменяющая исходную f(x), заданную таблично, и проходящая через все заданные точки – узлы интерполяции. Обычно в качестве функции L(x) выбирают полином, хотя через заданные точки можно провести любое количество функций. Линейное интерполирование предполагает учет только первых разностей. Это означает, что величины определяются по упрощенной формуле, в которой отброшены все члены более высокого порядка. Так, в формуле для линейной интерполяции надо сохранить только два слагаемых: Чтобы первое из отброшенных слагаемых
Этим именно и определяется условие применения линейной интерполяции. Левая часть неравенства состоит из двух сомножителей. Сомножитель
Вторая производная
Отсюда заключаем, что линейная интерполяция допустима, когда вторые разности не больше четырех единиц пятого десятичного знака: Ориентированные графы. Матричные методы разбиения орграфа без контуров на слои. Нахождение контуров в орграфах при анализе неплатежей. Выделение связных компонентов орграфа. Определение контуров в орграфе. Алгоритм устранения неплатежей. Граф – это математическая модель, с помощью которой удобно представлять бинарное отношение. Хотя теория графов получила свое развитие задолго до появления теории множеств как самостоятельной дисциплины, большое число задач теории отношений формулируются и решаются в рамках именно этой теории.
Если множество дуг не является симметричным отношением, то такой граф называется ориентированным графом. В своей жизни мы, так или иначе, соприкасались с объектами, имеющими структуру графа. К таким объектам относятся разного рода маршруты общественного транспорта: система метрополитена, автобусные маршруту и т.п. В частности, программисту знакома компьютерная сеть, также являющаяся графом (рис. 3.1). Общее здесь это наличие точек, соединенных линиями. Так в компьютерной сети точками являются отдельные серверы, а линиями – различные виды электрических сигналов. В метрополитене первое – станции, второе – туннели, проложенные между ними. В теории графов точки именуется вершинами, или узлами, а линии – ребрами, или дугами. Таким образом, граф – это совокупность вершин, соединённых ребрами. Вернемся к компьютерной сети. Она обладает определенной топологией, и может быть условно изображена в виде некоторого числа компьютеров и путей их соединяющих. На рисунке ниже в качестве примера показанаполносвязная топология. Пять компьютеров являются вершинами, а соединения (пути передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке. Вот некоторые важные обозначения, используемые в теории графов: G=(V, E), здесь G – граф, V – его вершины, а E – ребра; |V| – порядок (число вершин); |E| – размер графа (число рёбер). В нашем случае |V|=5, |E|=10; Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом. Если же граф связный, но это условие не выполняется, тогда такой граф называется ориентированным или орграфом. Ребра орграфа принято называть дугами. В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Степень входа вершины – количество входящих в эту вершину ребер, степень выхода – количество исходящих ребер. Сумма всех степеней графа равна удвоенному количеству всех его ребер.
|
||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 617; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.142.168 (0.009 с.) |


 .
. (а значит, и все последующие) не влияло заметно на точность интерполяции, его величина не должна превышать 0,5 единицы последнего десятичного знака функции. Применительно к пятизначным математическим таблицам это требование запишется так:
(а значит, и все последующие) не влияло заметно на точность интерполяции, его величина не должна превышать 0,5 единицы последнего десятичного знака функции. Применительно к пятизначным математическим таблицам это требование запишется так: .
. зависит от шага h, выбираемого при составлении таблицы. Обозначим этот сомножитель В: 2В = U2 — U. Экстремальное значение Вэ, при котором выполняется условие, найдем, взяв производную и приравняв ее нулю:
зависит от шага h, выбираемого при составлении таблицы. Обозначим этот сомножитель В: 2В = U2 — U. Экстремальное значение Вэ, при котором выполняется условие, найдем, взяв производную и приравняв ее нулю: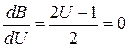 , откуда U = ½.
, откуда U = ½. показывает, что найден минимум и, следовательно,
показывает, что найден минимум и, следовательно, .
. . Указанное условие, как правило, выполняется в мореходных таблицах.
. Указанное условие, как правило, выполняется в мореходных таблицах.



