
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение критерия качества проекций в КДА и механизма расчета направляющих осей пространства дискриминантных функций.Содержание книги
Поиск на нашем сайте
1. К ритерии качества Определим интересующий нас показатель; 1. Если вектор Матрица суммарного внутриклассового расброса Напомним для дальнейшего, что ранг каждой матрицы Пример – Поскольку ранг каждой из
Тогда естественно определить второй член в (*) как
Как и выше очевидно что ранг матрицы Как будет показано немного ниже из этого следует что максимальная размерность пространства проекции из Хd в Уq будет не более чем К-1 То есть Проекция из d-мерного пространства в (К- 1)-мерное пространство осуществляется с помощью К- 1 разделяющих функций
Если считать
Выборки x1,..., хn проецируются на соответствующее множество выборок y1,..., yn которые можно описать с помощью их векторов средних значений
то можно непосредственно получить
Определим теперь интересующий нас показатель разделимости классов как отношение дисперсии межгрупповой к дисперсии в нутригрупповой (1) на интересующих нас новых координатах
Хороший показатель - чем он выше тем лучше разделяющие свойства данной линии у: чем>числитель тем дальше центры друг от друга, чем< знаменатель тем более компактны группы.
Уравнения (**) показывают, как матрицы разброса внутри класса и между классами отображаются посредством проекции в пространство меньшей размерности. Мы ищем матрицу отображения отношение разброса между классами к / разбросу внутри класса. Простым скалярным показателем разброса является определитель матрицы разброса. Определитель есть произведение собственных значений, Пользуясь этим показателем, получим функцию критерия
Задача нахождения прямоугольной матрицы
Несколько замечаний относительно этого решения. Во-первых, если То есть можем стандартно искать Однако в действительности так решать нежелательно, так как при этом потребуется ненужное вычисление матрицы
обобщенная задача определения СЗ, а затем решить
применить итерационный алгоритм вращения осей (метод Якоби) получим как и прежде в ФА диагон.
2. Размерность пространства дискриминационных функцийq
Можно дать 2 пояснения возможной величине q А). Первое по-проще – скорее на интуитивном уровне. Метод КДА образуя новое пространство размерности q задает там некий алгоритм распознавания новых объектов. Заметим что для определения положения новых координат используются по сути характеристики рассеяния и положения центров классов. Количество центров (точек-центроидов) =количеству классов К.
Отметим что если мы хотим с помощью некоторого количества точек задать положение некоторого пространства, то мерность этого пространства четко связана с минимально необходимым количеством таких точек: Для задания одномерного пространства – прямой надо 2 точки для двумерного – плоскости – 3 точки и т.д. То есть при наличии К точек (центров классов) мерность пространства которое мы можем задать с их помощью q=К-1. С поправкой на то что если количество классов К больше чем мерность d исходного пространства Х то тогда q негде набрать независимых координат больше чем d, в таком случае q=d Т.о. q = минимальному из чисел К-1 и d Б).Для определения
(убедитесь сами – матрицы То Так что не более К-1 собственных значений есть не нули и искомые векторы весовых функций соответствуют этим ненулевым собственным значениям. Что и дает мерность пространства - К-1 (с той же поправкой что и выше q = минимальному из чисел К-1 и d)
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.185.209 (0.009 с.) |

 проекций точек х на оси
проекций точек х на оси  и соответствующая им матрица отношения дисперсий
и соответствующая им матрица отношения дисперсий  .
. определен как строка матрицы
определен как строка матрицы  то есть
то есть  и
и 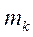 - к -тый центроид в Х,
- к -тый центроид в Х,  то матрица разброса (ковариаций) внутри к -того класса
то матрица разброса (ковариаций) внутри к -того класса 
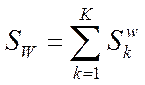

 образованной как внешнее произведение векторов (типа ВВТ)-не более 1. Докажите это.
образованной как внешнее произведение векторов (типа ВВТ)-не более 1. Докажите это. =
=  (*) и видим, что если вторую строку умножим на
(*) и видим, что если вторую строку умножим на  то получим первую строку. Т.о ранг (*) не более 1. и тд
то получим первую строку. Т.о ранг (*) не более 1. и тд не более единицы, и поскольку только К-1 из них – линейно независимы - (имея центры
не более единицы, и поскольку только К-1 из них – линейно независимы - (имея центры  и к-1 матрицу данных
и к-1 матрицу данных  …
…  возможно ввостановить
возможно ввостановить  . Покажите это) то ранг матрицы суммарного внутриклассового расброса
. Покажите это) то ранг матрицы суммарного внутриклассового расброса  не более К-1
не более К-1 2. Определим полный вектор средних значений в Х - m и полную матрицу разброса
2. Определим полный вектор средних значений в Х - m и полную матрицу разброса  :
:  и
и  Тогда
Тогда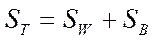 Так как известно что полный разброс
Так как известно что полный разброс  есть сумма разброса внутри класса
есть сумма разброса внутри класса  и разброса между классами
и разброса между классами  то
то - матрицу разброса между классами,:
- матрицу разброса между классами,:

 i =1,..., К- 1 (88)
i =1,..., К- 1 (88) составляющими вектора
составляющими вектора  , а векторы весовых функций
, а векторы весовых функций  столбцами матрицы
столбцами матрицы  размера d*(К-1), то проекцию можно записать в виде одного матричного уравнения
размера d*(К-1), то проекцию можно записать в виде одного матричного уравнения . (89)
. (89) и матриц разброса. Так, если мы определяем
и матриц разброса. Так, если мы определяем и
и 
 и
и 

 (**)
(**)
 - Известно как частное Релея
- Известно как частное Релея
 Очевидно что это
Очевидно что это а следовательно, и произведение «дисперсий» в основных направлениях, измеряющее объем гиперэллипсоида разброса.
а следовательно, и произведение «дисперсий» в основных направлениях, измеряющее объем гиперэллипсоида разброса. (2)
(2) , которая максимизирует
, которая максимизирует  по (1) или (2) – известное как частное Релея, сводится к нахождению обобщенных собственных векторов, соответствующим наибольшим собственным значениям в
по (1) или (2) – известное как частное Релея, сводится к нахождению обобщенных собственных векторов, соответствующим наибольшим собственным значениям в (**)
(**) — невырожденная матрица, то задачу, как и прежде, можно свести к обычной задаче определения собственного значения. То есть образуем из (**)
— невырожденная матрица, то задачу, как и прежде, можно свести к обычной задаче определения собственного значения. То есть образуем из (**)  или
или 
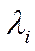 и
и  как СобствЧисла и СобВек матрицы
как СобствЧисла и СобВек матрицы 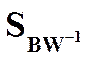 . Так мы можем решить задачу.
. Так мы можем решить задачу. . Вместо этого можно найти собственные значения как корни характеристического полинома (обобщенная задача определения СЗ)
. Вместо этого можно найти собственные значения как корни характеристического полинома (обобщенная задача определения СЗ) ,
, непосредственно для собственных векторов v i. Как решать далее дело вкуса в том числе можно
непосредственно для собственных векторов v i. Как решать далее дело вкуса в том числе можно собственных значений
собственных значений  и соответстующую ей матрицу преобразований (собственных векторов)
и соответстующую ей матрицу преобразований (собственных векторов) 
 решается
решается 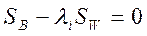 . В предположении что
. В предположении что 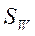 - невырожденная, то есть существует
- невырожденная, то есть существует  далее для определения количества ненулевых
далее для определения количества ненулевых  .
. Поскольку
Поскольку 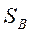 является суммой К матриц ранга единица или менее
является суммой К матриц ранга единица или менее - есть внешние произведения векторов (
- есть внешние произведения векторов ( -
-  ) и поскольку только К-1 из них независимые матрицы, - (матрицу последнего класса можно получить имея всю выборку и К-1 матрицу
) и поскольку только К-1 из них независимые матрицы, - (матрицу последнего класса можно получить имея всю выборку и К-1 матрицу  имеет ранг К-1 или меньше.
имеет ранг К-1 или меньше.


