
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
максимизировать распознающие качества искомого классификатора.⇐ ПредыдущаяСтр 11 из 11
Это есть механизм выбора оптимальной структуры пространства Х.
Процедура SPSS предоставляет возможность выбрать один из 5-ти вариантов формирования F-критерия (через “л ямбда ” Уилкс а”, раст. Махалонобиса, необъясненную дисперсию, наименьшее F-отношение, Расстояние V Pao) Как сказано выше выбранная форма F-критерия определит насколько улучшились (при введении нового признака) или ухудшились (при выведении ранее введенного в модель признака) разделяющие свойства пространства Х
Ниже рассмотрим эти варианты. Критерии шаговой процедуры ДА ( SPSS) для определения оптимального состава Х
В пакете SPSS для определения оптимального состава Х применяется шаговый алгорим включения-исключения c различными критериями качества разделимости классов в получаемой конфигурации переменных Х. Вариантов критериев предложено 5:
1. Критерий отбора переменных “л ямбда ” Уилкс а Wilks' lambda это отношение разброса точек внутри класса от средних в классах (внутригрупповая дисперсия) к общему разбросу точек от общего среднего (общей дисперсии).
Внутригрупповой расброс характеризует матрица ковариаций
Матрицу полного расброса Так как простым скалярным показателем расброса является определитель матрицы расброса то “л ямбда ” Уилкса” определяют как
Отбор переменных в шаговом дискриминантном анализе, для ввода в уравнение осуществляется на основании того, насколько они уменьшают значение "лямбда" Уилкса. На каждом шаге вводится переменная минимизирующая это значение Кроме того, SPSS проверяет уже включенные в модель переменные; та из них, которая имеет слишком маленькое значение F исключения, исключается.
где p - текущее значение количества переменных пространства Х n — общее число наблюдений,
2. Расстояние Махалонобиса Mahalonobis distance. На каждом шаге вводится переменная, максимизирующая расстояние Махалонобиса между ближайшими групповыми центрами. Расстояние между классами k1 и k2определяется по формуле:
Или в скалярном виде
3. Необъясненная дисперсия. На каждом шаге вводится переменная, минимизирующая сумму необъясненной изменчивости между группами. Необъясненная дисперсия между i и j классом понимается как (1-R2 ij), где R2 ij - коэффициент множественной корреляции, когда в качестве зависимой переменной рассматривается переменная, принимающая значения 0 и 1 в зависимости от того, в какую группу, i или j попадает наблюдение. Включается та переменная, которая минимизирует сумму необъясненных дисперсий 4/ Наименьшее F-отношение Smallest F-ratio. На каждом шаге вводится переменная, максимизирующая наименьшее F-отношение для пар классов (i и j), F-статистика равна:
5/ Расстояние V Pao. Rao's V distance
где р — число переменных в модели,K — число групп, nk — объем выборки k-й группы, Формирование версии F-критерий происходит подобним способом как в п.1 Выводы по КДА Еще раз отмечаем, что полученные КДФ непосредственно не решают проблему разделения классов (путаница в терминологии в том что дискриминантные функции переводятся как разделяющие функции) В результате работы КДА (или “множественного дискриминантного анализа”_ получают уменьшенной размерности Теперь, в уменьшенной размерности более точно возможно оцкнить отдельные ковариационные матрицы для каждого класса и использовать допущение (и проверить его) об общем нормальном многомерном распределении, что невозможно было бы (в силу большой размерности) сделать в исходном пространстве х. Становятся реальны и эффективны процедуры расчета расстояния Махалонобиса (снижается уровень проблем обращения матрицы ковариаций и получаем наилучший, с точки зрения критерия шаговой процедуры, состав х) для определения принадлежности к классу или вероятности класса для данного объекта х*.
Далее пройтись по методичке (файл описание работы с ДА в SPSS)Возможно расчитать результат КДА при раличных и общей матрице ковариайий при этом простые классифицирующие функции (ПКФ)– остаются без изменений (результаты расчета даются через РМ в КДФ и не совпадут с резудьтатами ПКФ) Нормальный дискриминантный анализ И так, на вопрос: как проводим классификацию в каноническом ДА мы знаем ответ – по минимуму меры М, М - мера Махаланобиса в пространстве КДФ У;. Но когда такая мера является наилучшей? – оказывется только в случае многомерного нормального распределения р(у) в классах (р(у/к) или рк(у)). Действительно, мы помним, что именно расстояние М от центра класса
где Мы вспомним [стр.консп 14 (принцип правдопобия)], что класс Далее учитываем что мы имеем не объект х, а у(х) (так как мы перешли в пространство КДФ), затем учтем(2*) и добавим предположение о равенстве ковариационных матриц в классах. Тогда очевидна что (**) - то же что (1*). Действительно в названных условиях подставляя(2*) в (**) замечаем что коэффициент при е для всех к – одинаков и для определения В связи с распространенностью случая нормальности распределения х (или у) в классах представляет серьезный интерес исследование вида границ между классами в таких системах данных. Эти результаты относят к т.н нормальному ДА, Ниже мы уже не будум останавливатся на проблемах исходной размерности х, считая, что используя КДА мы всегда можем перейти в пространство меньшей размерности у, и там применить механизвм НДА. Вопросы Раздедяющие функции и границы классов в нормальном дискриминантном анализе. Геометрическая интерпретация. Вывод простых классифицирующих функций Фишера. - на самост проработку – Р.Дуда П.Харт. Распознавание образов и анализ сцен. Стр. 36-42
|
||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.183 (0.016 с.) |
 Для записи формулы критерия определим:
Для записи формулы критерия определим: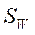
 Межгрупповой расброс - матрица
Межгрупповой расброс - матрица 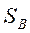 :
: можно вычислить как
можно вычислить как  или как
или как 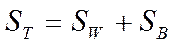

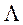 или что то-же - максимизирующая соответствующий F-критерий
или что то-же - максимизирующая соответствующий F-критерий F-значение для изменения в лямбде Уилкса при включении переменной в модель, содержащую р независимых переменных, равно:
F-значение для изменения в лямбде Уилкса при включении переменной в модель, содержащую р независимых переменных, равно: — лямбда Уилкса до включения новой переменной,
— лямбда Уилкса до включения новой переменной,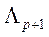 —лямбда Уилкса после включения новой переменной.
—лямбда Уилкса после включения новой переменной.
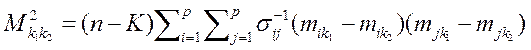



 —среднее x i-й переменной в k- й группе,
—среднее x i-й переменной в k- й группе,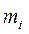 —среднее x i-й переменной по всем группам,
—среднее x i-й переменной по всем группам, 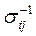 — элемент матрицы, обратной к ковариационной
— элемент матрицы, обратной к ковариационной 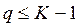 новое пространство признаков (КДФ
новое пространство признаков (КДФ 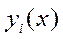 ), где состав
), где состав 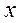 оптимизирован с помощью шаговой процедуры.
оптимизирован с помощью шаговой процедуры.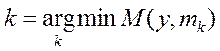 , (1*)
, (1*)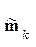 стоит в степени МНР рк(у):
стоит в степени МНР рк(у): (2*)
(2*)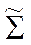 - матрица ковариаций КДФ
- матрица ковариаций КДФ  .
. объекта х в простейшем случае (при равных априорных вероятностях) определяем исходя из
объекта х в простейшем случае (при равных априорных вероятностях) определяем исходя из  (**)
(**) следует сравнивать только степени (2*) а там стоит
следует сравнивать только степени (2*) а там стоит 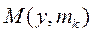 то есть получаем что из (**) следует
то есть получаем что из (**) следует  (1*).
(1*).



