
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Роль спектральной теоремы в решении задачи компонентного анализа
Но оказывается задачу КА поиска наибольших дисперсий по взаимно ортогональным направлениям возможно решить в терминах собственных значений и собственных векторов матрицы ковариаций – известно (из лин алг ебры) что для любой положительно определенной матрицы Выражение (**) называют спектральной теоремой или спектральным разложением матрицы Если в качестве
Тогда можно применить известный для нас механизм нахождения СЧ и СВ (вставка о сб.ч. и сб.в.) 1. решаем 2. затем в условие для собственного вектора подставляем Решая последовательно (**) для каждого Однако приведенные чисто алгебраические методы поиска
Посмотрите на рис 3 У данного элипса рассеяния недиагональная матрици ковариаций
Напомним что рассмотренный выше этап МГК где находятся эти новых компоненты называется компонентным анализом -КА 2. Этап МГК – выделение главных компонент
Построение главных компонент Именно они называются главными компонентами и именно их число Число главных компонент q Наиболее распространенных критерия выбора числа ГК – 2.
дисперсий - от ряда дисперсий 1 1 1 1 1 1 к кряду допустим 4 1 0.5 0.2 0.1 0.1 По данному критерию считается достаточным выбрать число компонент с величиной
по оси у- величина Количество компонент выбирается на том месте оси номеров компонент где излом графика наиболее резко переходит к основной затихающей тенднции:
|
|||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.104.173 (0.026 с.) |
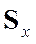 . Вернее более правильно так ------
. Вернее более правильно так ------ существует преобразование ее в диагональную матрицу
существует преобразование ее в диагональную матрицу  :
:  (**) причем ее диагональные элементы есть
(**) причем ее диагональные элементы есть  - собственные числа матрицы
- собственные числа матрицы  - матрица ее собственных ее векторов
- матрица ее собственных ее векторов пространства (на рис 5) из переменных
пространства (на рис 5) из переменных  , где
, где  - строки матрицы собств. векторов
- строки матрицы собств. векторов 
 – это условие нахождения собственных чисел
– это условие нахождения собственных чисел  и находим
и находим  (это одновременно наши наилучшие дисперсии)
(это одновременно наши наилучшие дисперсии)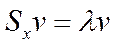 (*)
(*) 
 получая
получая 
 (**)
(**) находим все вектора
находим все вектора 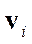 которые есть и направляющие линий проекции
которые есть и направляющие линий проекции 
 тоже не очень технологичны – например при 10-м порядке матрицы
тоже не очень технологичны – например при 10-м порядке матрицы  для получения
для получения  надо решать уравнение десятой степени и находить 10 его корней и тд.
надо решать уравнение десятой степени и находить 10 его корней и тд. Поэтому для нахожднния
Поэтому для нахожднния  применяют другой приближенный, но достаточно изящный подход
применяют другой приближенный, но достаточно изящный подход

 Если мы найдем целесообразный метод вращения координат то в результате найдутся новые положения осей как на рис 5 что в них элипс будет стоять уже как на рис 2 а значит в преобразованных координатах
Если мы найдем целесообразный метод вращения координат то в результате найдутся новые положения осей как на рис 5 что в них элипс будет стоять уже как на рис 2 а значит в преобразованных координатах  будем иметь диагональную ков. матрицу
будем иметь диагональную ков. матрицу  , где по диагонали стоят искомые дисперсии
, где по диагонали стоят искомые дисперсии  (собств. числа
(собств. числа  ) а итоговая матрицапреобразования
) а итоговая матрицапреобразования  в
в  будет искомой матрицей
будет искомой матрицей  собственных векторов и одновременно направляющими линий проекции
собственных векторов и одновременно направляющими линий проекции  .
.  Для вращения применяется метод Якоби.
Для вращения применяется метод Якоби.
 …
…  реализуется так, что полученные
реализуется так, что полученные  и соответственно
и соответственно  используют в дальнейшем для анализа.
используют в дальнейшем для анализа. 1.Критерий Кайзера (Kaiser, 1960) Основан на учете того, что процедуры преобразования проводятся не с ковариционной а с корелляционной матрицей
1.Критерий Кайзера (Kaiser, 1960) Основан на учете того, что процедуры преобразования проводятся не с ковариционной а с корелляционной матрицей  – где по диагонили (дисперсии) стоят 1.
– где по диагонили (дисперсии) стоят 1. Таким образом в преобразованной матрице
Таким образом в преобразованной матрице  . Здесь это 2 компоненты.
. Здесь это 2 компоненты. 2. Другой распространенный критерий – критерий Кэттеля (Cattell,1966) или критерий каменистой оссыпи. Строят зависимость:
2. Другой распространенный критерий – критерий Кэттеля (Cattell,1966) или критерий каменистой оссыпи. Строят зависимость: по оси х – номер компон.
по оси х – номер компон.  .
.


