Далее для механизма классификации идеология та же что и в нда

В новом пространстве осей (переменных) можно

- получить разделяющие (желательно линейные) поверхности делящие пространство на области классов, или

- просто вычислять уже в этом пространстве растояние Махаланобиса от точки до центра класс а и отнести точку к классу по минимуму этого расстояния, или

- рассчитать вероятности классов если приняли

А) конкретную гипотезу о виде плотности распределения в классах - (как правило гипотезу о нормальности распределения) и –

Б) предположение о равенстве в классах

Приведенные интуитивные действия могут быть формализованы математически и реализованы в подходящем алгоритме если

выбрать подходящий критерий качества для положения осей проекции когда оцениваем эффективность проектирования точек и сокращения размерности пространства .для разделения классов.

 

Данный механизм – предмет канонического ДА.

А вот теперь поняв главную идею КДА – для того чтобы понять как

– как находяться линии проекции в КДА

было бы полезно познакомится с методом главных компонент – частью ФА, где для нахождения осей проекции применен близкий по идям подход но в упрощенном виде.

МГК нам все равно нужен в ФА, а после него проще рассказать, как искать линии наилучших проекций в КДА.

Поэтому временно отвлечемся от задачи разделения

и рассммотрим

 

Факторный Анализ

Метод главных компонент

МГК состоит из 2-х этапов –

Компонентный анализ и 2. Выделение главных компонент

Компонентный анализ

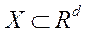З адача следующая: Имеется пространство в котором задана выборки (единый элипс рассеяния). Необходимо найти новые взаимно ортогональные оси так, чтобы дисперсии проекций точек на были максимальны:

- вдоль первой надо получать максим. по сумме расброса точек

- – д.б. ортогональна и при этом иметь вдоль себя также проекции с макс. расбросом и т.д. до с

Вспомним варианты расположения эллипса рассеяния в координатах

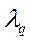
На рис 1 - круг рассеяния – х -ы независимы и дисперсии по каждой оси одинаковы – на какую новую ось не проектируй – получишь те же шарики – вид сбоку.

На рис 2. х -ы независимы, то есть матрица ковариаций диагональная. Оси эллипса рассеяния расположены паралельно осям координат - поэтому в данном случае мы имеем уже решенную задачу КА – так как оси рассеяния элипса паралельны осям координат х и удовлетворяют условиям задачи КА

Теперь нам понятна задача КА–

Когда имеем общий случай элипса рассеяния в Х – рис 3 и матрица ковариаций недиагональна то нашей целью есть получить новые координаты в У

такие чтобы все выглядело в них как на рис 2.

То есть сначила найти ось у₁ по макс. расброса рис 4 Затем ортоганальную ей у₂ по макс расброса рис 5. и так далее с тем чтобы получить в новых координатах у рис 5 положение элипса рассеяния так как оно расположено в старых координатах х на рис. 2