
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общее и различия в постановке задач кластерного, факторного,Стр 1 из 11Следующая ⇒
Общее и различия в постановке задач кластерного, факторного, Пример Основная гипотеза методов РО исходит того что пространство признаков подобрано целесообразно и поэтому концентрпрует в себе различия классов – а значит и отличия их средних. Поэтому основная гипотеза РО – гипотеза компактности классов в Х. Но что же происходит при наличии подклассов – см самый неприятный вариант.
Здесь средние классов совпадают и применяемый алгоритм должен строить сложную нелинейную границу. Если же выделить подклассы то задачу можно решить линейными границами.
Поэтому ваш кластерный анализ проводится сначала в полной матрице (важно – совпадут группировки по кластерам с нашими известными классами – если нет, то какие будут отличия и насколько значимы будут они) а затем проанализировать тоже самое но в каждом классе отдельно – не наблюдаются ли у нас явные подклассы
Затем прогоним данные через ЛР и получите бинарные классификаторы Затем тоже дискриминантным анализом, И завершим все поверкой как группируются наши признаки в этой задаче – то есть проведем факторный анализ. (логичнее было бы это сделатьв начале - до ЛГ и ДА но …..не играет особой роли) Особо любопытные попробуют провести клиссификацию уже не в исходном пространстве а в пространстве факторов (и канонических ДФ построенных на факторах) Это наша программа максимум на практических занятиях – и в сумме эта работа будет Вашей иллюстрацией к вопросам на экзамене. Начнем теперь с Этапа постановки задачи. Постановка задачи классификации (с учителем) 1. Задан факт существования некоторого множества классов 2. известен факт, что множества 3. Н ам классы где Очевидно что ввиду (*) для любых подмножеств удовлетворяющих (**) должно выполнятся
Особенности условий вероятностной и детерминированных Плюсы подхода –1. все проблемы - решаем одним классификатором. 2. Однозначность классификации (качество – другой вопрос) Минус подхода - как правило классификатор должен быть сложным, нелинейным - такой сделать качественным очень сложно
Примеры А) “один против всех” строится так чтобы
Распознающая система К классов состоит из построенных независимо друг от друга К функций Поэтому существует механизм возникновения неопределенных ситуаций Во первых - некоторые из рассматриваемых подходов совпадают при определенных условия и понимание этого на идейном уровне полезно сразу – до подробного изложения материала. Во вторых –материал будучи идейно понятным, в математическом представлении не всегда такой же прозрачный. Для того чтобы разобраться, нам придется привлекать (вспоминать) некоторые дополнительные сведения из аналитической геометрии и линейной алгебры. Это потребует времени. Однако на практ. занятиях желательно работать сразу до того как мы разжуем всю теорию. Это мы сможем если в общих чертах будем представлять основные подходы ДА. После обзора, мы, насколько успеем, – ровно настолько пройдем углубленно рассмотренную раннее схему методов ДА. Что не успеем перенесем в более углубленные магистерские курсы по математическому моделированию. Смотрим схему - Слева у нас - Байесовский подход.
1. Для расчета искомых вероятностей
2.Исходя из принципа правдоподобия решение о классе для точки З наменатель в (*) одинаков, поэтому для определения класса можем решать более простую задачу, не расчитывая вероятность
А при равных Апрорн Вероятностях формула имеет срвсем простой вид У словную Аналогии метода наибольшего правдоподобия в ТВ и методов оптимизации в детерминированной постановке мы рассмотрим при подробном изложении.
Это будет очевидно когда в (**) будем подставлять вид Расстояние Махаланобиса
имеем следующую картину – элипсы рассеяния ориентированы одинаково в классах но произвольно по направлениям.
Мы также видим что при равенстве Эвклидова расстояний от центров классов до точки х - точка более близка к границе 2-го класса
Для того чтобы эта близость следовала из меры расстояния до центров классов ее необходимо скорректировать подобным же образом как и в предыдущем случае, - но используя не только даигональные элементы матрицы ковариаций – дисперсии, а всю матрицу ковариаций целиком. Формула расстояния до центра класса теперь по аналогии с предыдущим случаем (но с учетом общего направления рассеяния) выглядит так
где
6. Ну и понятно что при неравенстве матриц ковариаций в классах будем иметь свою формулу расстояния до соответствующего класса.
0 Вы уже заметили – что мы корректировали формулу расстояния с тем чтобы точку присвоить тому классу, граница рассеяния которой ближе к точке х - Вы уже поняли что методы построения формул границ и методы построения формул расстояний до центров имеют в своей основе нечто общее а именно - построение формулы общности класса – и в этом Обоснование нормального ДА Введя расстояние Махаланобиса мы пришли на распутье НДА и КДА. Расстояние Махалонобиса в предположении о нормальности распределения х полностью совпадает с показателем степени в многомерном нормальном распределении (МНР) Факторный Анализ Метод главных компонент МГК состоит из 2-х этапов – Компонентный анализ З адача следующая: Имеется пространство
- Вспомним варианты расположения эллипса рассеяния в координатах
такие чтобы все выглядело в них как на рис 2. То есть сначила найти ось у1 по макс. расброса Однако Так мы найдем только первую главную компоненту. – ту вдоль которой имеется наибольший расброс точек в Х - рис. 4. Но нам надо найти и другие компоненты – А вторая компонента Для того чтобы решить эту задачу надо вычислить остатки
Задача посложнее – доп операции по вычислению остатков и учет дополнительного ограничения (*) Далее – для третьей оси - снова вычисление остатков и новая поцедура поиска уже вектора Все это не очень технологично.
Число главных компонент q Наиболее распространенных критерия выбора числа ГК – 2.
дисперсий - от ряда дисперсий 1 1 1 1 1 1 к кряду допустим 4 1 0.5 0.2 0.1 0.1 По данному критерию считается достаточным выбрать число компонент с величиной
по оси у- величина Количество компонент выбирается на том месте оси номеров компонент где излом графика наиболее резко переходит к основной затихающей тенднции: Внимание Выводы по ФА Аппарат ФА - достаточно субъективен (за что его и критикуют). Вращение чаще применяют ортогональное (в SPSS-“варимакс”) - полученные Главные Компоненты вращают, оставляя их при этом взаимно ортогональными и косоугольное, допуская их не ортогональность – лишь бы полученные факторы были тесно кореллированы с образуемой “группой влияния” Х-ов, Общий принцип – лишь бы попасть на красивую интерпретацию факторов как латентной причины группы “по интересам” следствий – х -ов. Однако плюсы ФА перевешивают минусы – симбиоз грамотного предметного специалиста и математического аппарата ФА часто попадает в цель и получают очень красиво интерпретируемые результаты внутренней структуры изучаемого явления. Из-за недостатка времени и указаной субъективности аппарата вращения мы не будем подробно останавливатся на всех разновидностях механизма образования факторов – с ними коротко можно познакомится в самоучителе по ssps, а мы прогоним на практике через ФА в ssps, наши данные и посмотрим результаты группировки переменных в факторы. Резюме – инструмент ФА – это инструмент выявления скрытых латентных причин (факторов F) каждый из которых должен наилучшим образом объяснять нам изменения, вариации в переменных (следствиях, признаках) х в корреллированных “по интересам” группах х -ов
Канонический ДА Хороший показатель - чем он выше тем лучше разделяющие свойства данной линии у: чем>числитель тем дальше центры друг от друга, чем< знаменатель тем более компактны группы. Уравнения (**) показывают, как матрицы разброса внутри класса и между классами отображаются посредством проекции в пространство меньшей размерности. Мы ищем матрицу отображения отношение разброса между классами к / разбросу внутри класса. Простым скалярным показателем разброса является определитель матрицы разброса. Определитель есть произведение собственных значений, Пользуясь этим показателем, получим функцию критерия
Задача нахождения прямоугольной матрицы
Несколько замечаний относительно этого решения. Во-первых, если
То есть можем стандартно искать Однако в действительности так решать нежелательно, так как при этом потребуется ненужное вычисление матрицы
обобщенная задача определения СЗ, а затем решить
применить итерационный алгоритм вращения осей (метод Якоби) получим как и прежде в ФА диагон.
2. Размерность пространства дискриминационных функцийq
Можно дать 2 пояснения возможной величине q А). Первое по-проще – скорее на интуитивном уровне. Метод КДА образуя новое пространство размерности q задает там некий алгоритм распознавания новых объектов. Заметим что для определения положения новых координат используются по сути характеристики рассеяния и положения центров классов. Количество центров (точек-центроидов) =количеству классов К. Отметим что если мы хотим с помощью некоторого количества точек задать положение некоторого пространства, то мерность этого пространства четко связана с минимально необходимым количеством таких точек: Для задания одномерного пространства – прямой надо 2 точки для двумерного – плоскости – 3 точки и т.д. То есть при наличии К точек (центров классов) мерность пространства которое мы можем задать с их помощью q=К-1. С поправкой на то что если количество классов К больше чем мерность d исходного пространства Х то тогда q негде набрать независимых координат больше чем d, в таком случае q=d Т.о. q = минимальному из чисел К-1 и d Б).Для определения
(убедитесь сами – матрицы То Так что не более К-1 собственных значений есть не нули и искомые векторы весовых функций соответствуют этим ненулевым собственным значениям. Что и дает мерность пространства - К-1 (с той же поправкой что и выше q = минимальному из чисел К-1 и d) Выводы по КДА Еще раз отмечаем, что полученные КДФ непосредственно не решают проблему разделения классов (путаница в терминологии в том что дискриминантные функции переводятся как разделяющие функции) В результате работы КДА (или “множественного дискриминантного анализа”_ получают уменьшенной размерности Теперь, в уменьшенной размерности более точно возможно оцкнить отдельные ковариационные матрицы для каждого класса и использовать допущение (и проверить его) об общем нормальном многомерном распределении, что невозможно было бы (в силу большой размерности) сделать в исходном пространстве х. Становятся реальны и эффективны процедуры расчета расстояния Махалонобиса (снижается уровень проблем обращения матрицы ковариаций и получаем наилучший, с точки зрения критерия шаговой процедуры, состав х) для определения принадлежности к классу или вероятности класса для данного объекта х*. Далее пройтись по методичке (файл описание работы с ДА в SPSS)Возможно расчитать результат КДА при раличных и общей матрице ковариайий при этом простые классифицирующие функции (ПКФ)– остаются без изменений (результаты расчета даются через РМ в КДФ и не совпадут с резудьтатами ПКФ) Нормальный дискриминантный анализ И так, на вопрос: как проводим классификацию в каноническом ДА мы знаем ответ – по минимуму меры М, М - мера Махаланобиса в пространстве КДФ У;. Но когда такая мера является наилучшей? – оказывется только в случае многомерного нормального распределения р(у) в классах (р(у/к) или рк(у)). Действительно, мы помним, что именно расстояние М от центра класса
где Мы вспомним [стр.консп 14 (принцип правдопобия)], что класс Далее учитываем что мы имеем не объект х, а у(х) (так как мы перешли в пространство КДФ), затем учтем(2*) и добавим предположение о равенстве ковариационных матриц в классах. Тогда очевидна что (**) - то же что (1*). Действительно в названных условиях подставляя(2*) в (**) замечаем что коэффициент при е для всех к – одинаков и для определения В связи с распространенностью случая нормальности распределения х (или у) в классах представляет серьезный интерес исследование вида границ между классами в таких системах данных. Эти результаты относят к т.н нормальному ДА, Ниже мы уже не будум останавливатся на проблемах исходной размерности х, считая, что используя КДА мы всегда можем перейти в пространство меньшей размерности у, и там применить механизвм НДА. Вопросы Раздедяющие функции и границы классов в нормальном дискриминантном анализе. Геометрическая интерпретация. Вывод простых классифицирующих функций Фишера. - на самост проработку – Р.Дуда П.Харт. Распознавание образов и анализ сцен. Стр. 36-42
Общее и различия в постановке задач кластерного, факторного,
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.77.98 (0.114 с.) |

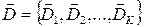 , представляющих собой конечные или бесконечные множества объектов:
, представляющих собой конечные или бесконечные множества объектов: 
 …..
…..  .
. Æ при
Æ при  (*)!
(*)! задаются как их приближения
задаются как их приближения  через усеченные множества объектов, им принадлежащих
через усеченные множества объектов, им принадлежащих  ,
,  ,…,
,…,  или
или  ,
,  ,…,
,…, 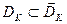 (**)
(**)
 ,….,
,…., 
 Æ при
Æ при  4. Предполагается что данные объекты, описываются в конечномерном пространстве
4. Предполагается что данные объекты, описываются в конечномерном пространстве  вектором признаков
вектором признаков  что образует в пространстве
что образует в пространстве  соответствующие множества
соответствующие множества 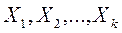 .
. Необходимо на основании обучающих подмножеств
Необходимо на основании обучающих подмножеств 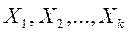 построить наилучшее правило классификации произвольного объекта из исходных множеств
построить наилучшее правило классификации произвольного объекта из исходных множеств  .
.
 Решение о принадлежности точки
Решение о принадлежности точки  классу
классу  принимается при
принимается при и
и 


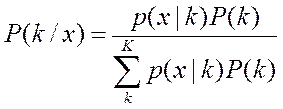
 Мы позже пройдемся по Байесу подробнее, он того стоит, а сейчас пользуясь тем что вы о БП говорили ранее, я буду использовать основные понятия БП, как Вам известные Итак Байесовский подход в РаспОбр наиболее распространенный вариант - вероятностного подхода, так как в самом общем виде (“общее”, так сказать, не придумаешь) дает формулу пересчета априорной вероятности в апостериорную, что при наличии составляющих этой формулы, дает оценку вероятности появления каждого из
Мы позже пройдемся по Байесу подробнее, он того стоит, а сейчас пользуясь тем что вы о БП говорили ранее, я буду использовать основные понятия БП, как Вам известные Итак Байесовский подход в РаспОбр наиболее распространенный вариант - вероятностного подхода, так как в самом общем виде (“общее”, так сказать, не придумаешь) дает формулу пересчета априорной вероятности в апостериорную, что при наличии составляющих этой формулы, дает оценку вероятности появления каждого из 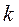 классов в конкретной точке пространства признаков
классов в конкретной точке пространства признаков 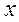 :
: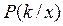 нужно иметь, априорные вероятности
нужно иметь, априорные вероятности 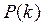 и условные плотности обозначаемые
и условные плотности обозначаемые 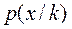 или
или 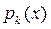 - это плотности
- это плотности 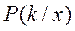 по (*) выше всех в точке х – то есть максимальна.
по (*) выше всех в точке х – то есть максимальна.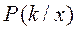 а принимая решение по максимуму числителя
а принимая решение по максимуму числителя (1)
(1)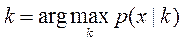 (2)
(2) плотность или ее взвешеный вариант
плотность или ее взвешеный вариант 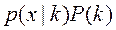 называют правдоподобием.
называют правдоподобием. Пользуясь тем, что логарифмирование зависимостей не меняет точки эстремумов исследуемых функционалов – (log,ln – фукции дифференцируемые и монотонно возрастающие) правдоподобие логарифмируют получая часто более простые выражения (**):
Пользуясь тем, что логарифмирование зависимостей не меняет точки эстремумов исследуемых функционалов – (log,ln – фукции дифференцируемые и монотонно возрастающие) правдоподобие логарифмируют получая часто более простые выражения (**):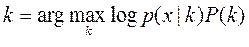 и
и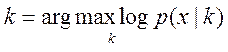 (**)
(**)
 Если координаты зависимы – и рассеяния в классах одинаковы, то ков ариационные матрицы в классах равны и недиагональны (обозн
Если координаты зависимы – и рассеяния в классах одинаковы, то ков ариационные матрицы в классах равны и недиагональны (обозн 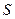 или
или  )
)

 - обратная матрица ковариаций. Эта общая формула расстояния носит название индийского математика Махаланобиса.
- обратная матрица ковариаций. Эта общая формула расстояния носит название индийского математика Махаланобиса.


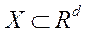 в котором задана выборки
в котором задана выборки  (единый элипс рассеяния). Необходимо найти новые взаимно ортогональные оси
(единый элипс рассеяния). Необходимо найти новые взаимно ортогональные оси 
 так, чтобы дисперсии
так, чтобы дисперсии  проекций точек
проекций точек  на
на  были максимальны:
были максимальны:

 - вдоль первой
- вдоль первой  надо получать максим. по сумме расброса точек
надо получать максим. по сумме расброса точек 
 – д.б. ортогональна
– д.б. ортогональна  и т.д. до
и т.д. до  с
с 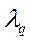


 На рис 1 - круг рассеяния – х -ы независимы и дисперсии по каждой оси одинаковы – на какую новую ось не проектируй – получишь те же шарики – вид сбоку.
На рис 1 - круг рассеяния – х -ы независимы и дисперсии по каждой оси одинаковы – на какую новую ось не проектируй – получишь те же шарики – вид сбоку. На рис 2. х -ы независимы, то есть матрица ковариаций диагональная. Оси эллипса рассеяния расположены паралельно осям координат - поэтому в данном случае мы имеем уже решенную задачу КА – так как оси рассеяния элипса паралельны осям координат х и удовлетворяют условиям задачи КА
На рис 2. х -ы независимы, то есть матрица ковариаций диагональная. Оси эллипса рассеяния расположены паралельно осям координат - поэтому в данном случае мы имеем уже решенную задачу КА – так как оси рассеяния элипса паралельны осям координат х и удовлетворяют условиям задачи КА Теперь нам понятна задача КА–
Теперь нам понятна задача КА– Когда имеем общий случай элипса рассеяния в Х – рис 3 и матрица ковариаций недиагональна то нашей целью есть получить новые координаты в У
Когда имеем общий случай элипса рассеяния в Х – рис 3 и матрица ковариаций недиагональна то нашей целью есть получить новые координаты в У рис 4 Затем ортоганальную ей у2 по макс расброса
рис 4 Затем ортоганальную ей у2 по макс расброса  рис 5. и так далее с тем чтобы получить в новых координатах у рис 5 положение элипса рассеяния так как оно расположено в старых координатах х на рис. 2
рис 5. и так далее с тем чтобы получить в новых координатах у рис 5 положение элипса рассеяния так как оно расположено в старых координатах х на рис. 2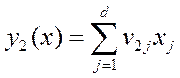 , будучи ортогональна первой должна иметь направление при этом вдоль максимального расброса в оставшихся направлениях пространства
, будучи ортогональна первой должна иметь направление при этом вдоль максимального расброса в оставшихся направлениях пространства и для них, как ранее на х- ах, построить матрицу ковариаций
и для них, как ранее на х- ах, построить матрицу ковариаций 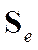 и снова решить задачу макс. уже
и снова решить задачу макс. уже  при условии нормировки
при условии нормировки 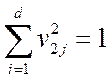 и ортоганальности
и ортоганальности  (*)
(*)
 . В целом имеем серию процедур последовательной максимизации
. В целом имеем серию процедур последовательной максимизации 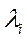 -
- 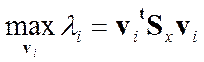 на дисперсии остатков от процедуры N =(
на дисперсии остатков от процедуры N =(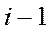 ) при условии н нормировки
) при условии н нормировки 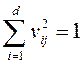 и учета условия ортогональности векторов
и учета условия ортогональности векторов 

 1.Критерий Кайзера (Kaiser, 1960) Основан на учете того, что процедуры преобразования проводятся не с ковариционной а с корелляционной матрицей
1.Критерий Кайзера (Kaiser, 1960) Основан на учете того, что процедуры преобразования проводятся не с ковариционной а с корелляционной матрицей  – где по диагонили (дисперсии) стоят 1.
– где по диагонили (дисперсии) стоят 1. Таким образом в преобразованной матрице
Таким образом в преобразованной матрице  , где на диагонали тоже будут стоять дисперсии – их величина отражает относительное перераспределение
, где на диагонали тоже будут стоять дисперсии – их величина отражает относительное перераспределение . Здесь это 2 компоненты.
. Здесь это 2 компоненты. 2. Другой распространенный критерий – критерий Кэттеля (Cattell,1966) или критерий каменистой оссыпи. Строят зависимость:
2. Другой распространенный критерий – критерий Кэттеля (Cattell,1966) или критерий каменистой оссыпи. Строят зависимость: по оси х – номер компон.
по оси х – номер компон.  .
. , которая максимизирует
, которая максимизирует а следовательно, и произведение «дисперсий» в основных направлениях, измеряющее объем гиперэллипсоида разброса.
а следовательно, и произведение «дисперсий» в основных направлениях, измеряющее объем гиперэллипсоида разброса. (2)
(2) , которая максимизирует
, которая максимизирует  по (1) или (2) – известное как частное Релея, сводится к нахождению обобщенных собственных векторов, соответствующим наибольшим собственным значениям в
по (1) или (2) – известное как частное Релея, сводится к нахождению обобщенных собственных векторов, соответствующим наибольшим собственным значениям в (**)
(**) — невырожденная матрица, то задачу, как и прежде, можно свести к обычной задаче определения собственного значения. То есть образуем из (**)
— невырожденная матрица, то задачу, как и прежде, можно свести к обычной задаче определения собственного значения. То есть образуем из (**)  или
или 
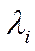 и
и  как СобствЧисла и СобВек матрицы
как СобствЧисла и СобВек матрицы 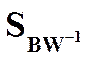 . Так мы можем решить задачу.
. Так мы можем решить задачу. . Вместо этого можно найти собственные значения как корни характеристического полинома (обобщенная задача определения СЗ)
. Вместо этого можно найти собственные значения как корни характеристического полинома (обобщенная задача определения СЗ) ,
, непосредственно для собственных векторов v i. Как решать далее дело вкуса в том числе можно
непосредственно для собственных векторов v i. Как решать далее дело вкуса в том числе можно матрицу
матрицу собственных значений
собственных значений  и соответстующую ей матрицу преобразований (собственных векторов)
и соответстующую ей матрицу преобразований (собственных векторов) 
 решается
решается 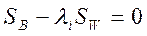 . В предположении что
. В предположении что 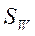 - невырожденная, то есть существует
- невырожденная, то есть существует  далее для определения количества ненулевых
далее для определения количества ненулевых  .
. Поскольку
Поскольку 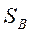 является суммой К матриц ранга единица или менее
является суммой К матриц ранга единица или менее - есть внешние произведения векторов (
- есть внешние произведения векторов ( -
-  ) и поскольку только К-1 из них независимые матрицы, - (матрицу последнего класса можно получить имея всю выборку и К-1 матрицу
) и поскольку только К-1 из них независимые матрицы, - (матрицу последнего класса можно получить имея всю выборку и К-1 матрицу  имеет ранг К-1 или меньше.
имеет ранг К-1 или меньше.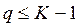 новое пространство признаков (КДФ
новое пространство признаков (КДФ 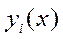 ), где состав
), где состав 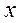 оптимизирован с помощью шаговой процедуры.
оптимизирован с помощью шаговой процедуры.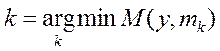 , (1*)
, (1*)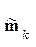 стоит в степени МНР рк(у):
стоит в степени МНР рк(у): (2*)
(2*)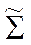 - матрица ковариаций КДФ
- матрица ковариаций КДФ  .
.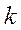 объекта х в простейшем случае (при равных априорных вероятностях) определяем исходя из
объекта х в простейшем случае (при равных априорных вероятностях) определяем исходя из  (**)
(**) следует сравнивать только степени (2*) а там стоит
следует сравнивать только степени (2*) а там стоит 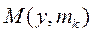 то есть получаем что из (**) следует
то есть получаем что из (**) следует  (1*).
(1*).



