
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для доказательства строим отдельно области, соответствующие левой и правой частям данного выражения. Если построенные области совпадают, то закон считается доказанным.
На рис.1.1а показана область, соответствующая левой части выражения. Здесь вертикальная штриховка соответствует пересечению На рис.1.1б изображена область, соответствующая правой части выражения. Здесь вертикальная штриховка соответствует объединению
а) б) Рис.1.1 Сравнение полученных областей показывает, что они совпадают, т.е. закон доказан. Примеры для самостоятельного решения 1. В трехэлементном множестве M = {a,b,c} Операция задана таблицей Кэли
Определить тип алгебры. Указать нейтральный и обратные Элементы, если они существуют. 2. Дана группа A=<M, +>, где M={a, b, c, d, e, f}, а аддитивная операция задана таблицей Кэли
Является ли данная группа коммутативной? Какой элемент из M играет роль нейтрального элемента? Для каждого элемента из M определитель обратный элемент. 3. К какому типу относится алгебра A=<R, Указать тип алгебры, которую образует множество целых чисел с заданными в нем операциями сложения и умножения. 5. На множестве M={a,b,c} заданы аддитивная и мультипликативная операции таблицами Кэли:
Показать, что M с заданными в нем операциями образует коммутативное тело. Для элементов из M определить нейтральные и обратные элементы относительно заданных операций. Заменить элементы a, b, c соответственно на числа 1,2,3 и истолкуйте заданные операции в числовом множестве. Доказать закон дистрибутивности пересечения относительно объединения. Доказать закон идемпотентности пересечения. Доказать закон де Моргана
Доказать закон де Моргана
С помощью кругов Эйлера. Доказать, что
СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВА Множество M при фиксированных независимых подмножествах
где называется первичным термом, а
называется конституантой.
Пояснение. Каждое фиксированное множество
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.197.123 (0.006 с.) |
 , а горизонтальная штриховка - Ma. Тогда вся заштрихованная область будет соответствовать объединению этих областей, т.е.
, а горизонтальная штриховка - Ma. Тогда вся заштрихованная область будет соответствовать объединению этих областей, т.е. 
 , а горизонтальная штриховка -
, а горизонтальная штриховка -  . Тогда область, в которой встречаются обе штриховки, будет соответствовать пересечению
. Тогда область, в которой встречаются обе штриховки, будет соответствовать пересечению 


 аддитивная
аддитивная

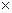 >, являющаяся совокупностью множества действительных чисел с заданной в нем операцией умножения.
>, являющаяся совокупностью множества действительных чисел с заданной в нем операцией умножения.

 .
. .
. .
. универсального множества J, т.е.
универсального множества J, т.е.  можно задать в виде объединения конституант
можно задать в виде объединения конституант ,
,



 ,
, 
 разбивает пространство J на две части: на собственно
разбивает пространство J на две части: на собственно 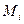 и на
и на  . При независимых множествах
. При независимых множествах  пространственно разбивается на
пространственно разбивается на  =
=  областей. Каждая область является пересечением n множеств
областей. Каждая область является пересечением n множеств  . Этой области можно сопоставить двоичный вектор
. Этой области можно сопоставить двоичный вектор  , в котором
, в котором  , если в конституанту
, если в конституанту  входит
входит  , если входит
, если входит  . (2.1)
. (2.1)


