Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множество m В пространстве j можно задать В виде объединения этих областей, Т. Е. Конституант. Графическим изображением указанного объединения является диаграмма Венна.
Множество M можно задать двоичным вектором длины 2n, в котором
Пространство J, в котором задано множество M, можно задать с помощью гиперкуба или n-мерного куба (n – размерность пространства, равная числу фиксированных множеств). Каждая вершина гиперкуба взаимно однозначно соответствует области пространства, и две вершины соединены ребром (имеющим общую границу). Сопоставленные этим областям двоичные векторы отличаются в одном и только одном разряде. Множество M можно задать в виде двоичной таблицы, каждой строке которой взаимно однозначно соответствует конституанта. Множество строк таблицы линейно упорядочено по возрастанию десятичного эквивалента соответствующего двоичного набора. Столбцам соответствуют множества, образующие пространство, последний столбец сопоставляется множеству M, и единица указывает на вхождение соответствующей конституанты в множество M. Пример 1. В трехмерном пространстве 1. Для представления заданного множества M в виде двоичного вектора воспользуемся формулой (2.2), где коэффициент Так как
Теперь необходимо подобрать коэффициенты 217 = 1.27+1.26+0.25+1.24+1.23+0.22+0.21+1.20. Множество найденных коэффициентов и является двоичным вектором, т.е. V=(1,1,0,1,1,0,0,1). Определить коэффициенты
2. Построение диаграммы Венна начинается с разбиения пространства J на 2n областей с помощью n фигур (замкнутых линий), где n – число различных множеств, входящих в J. При этом каждая последующая фигура должна иметь одну и только одну общую область с каждой из ранее построенных фигур. Такое разбиение называют символом Венна. По условию задачи При n=1 пространство разбивается на две области (рис.2.1а). При этом общей областью пространства J и множества M является само множество M. При n=2, т.е. При n=3, т.е.
Каждой из областей (конституант) можно сопоставить двоичный вектор W длины n, который представим в виде десятичного эквивалента d(c) по формуле (2.1). С другой стороны,
Определяя коэффициенты 0 = 0.22 + 0.21 + 0.20. Тем самым мы определили двоичный вектор W0 = (0,0,0), соответствующий рассматриваемой области. Учитывая, что компонента 0 (
Тогда, учитывая, что единица в двоичном векторе V означает включение соответствующей области в множество M, а нуль – исключение, построим диаграмму Венна. Заданное (отмечено штриховкой) множество M изображено на рис.2.2.
Рис.2.2
|
||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.144.217 (0.007 с.) |
 разряду соответствуют область с десятичным эквивалентом, равным
разряду соответствуют область с десятичным эквивалентом, равным 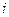 . Вектор, определяющий множество M, представим в виде десятичного эквивалента
. Вектор, определяющий множество M, представим в виде десятичного эквивалента ,
,  (2.2)
(2.2) множество
множество  задано десятичным эквивалентом d(M)=217. Задать множество M: 1. двоичным вектором, 2. диаграммой Венна, 3. таблицей, 4. гиперкубом, 5. аналитическим выражением.
задано десятичным эквивалентом d(M)=217. Задать множество M: 1. двоичным вектором, 2. диаграммой Венна, 3. таблицей, 4. гиперкубом, 5. аналитическим выражением. принимает значение 0 или 1, 2n – длина двоичного вектора (число разрядом), n – число множеств в пространстве J.
принимает значение 0 или 1, 2n – длина двоичного вектора (число разрядом), n – число множеств в пространстве J. . Тогда
. Тогда
 принимающие значение 0 или 1, такие, что сумма в правой части записанного выражения была равна 217. В результате мы получим
принимающие значение 0 или 1, такие, что сумма в правой части записанного выражения была равна 217. В результате мы получим
 (компоненты вектора) можно с помощью правила перевода целых десятичных чисел в двоичные. Перевод осуществляется последовательным делением исходного числа (в нашем случае 217) и каждого частного на два. Получаемые при этом остатки (0 или 1), записанные в обратном порядке, дают представление десятичного числа в двоичной системе счисления (в нашем случае компоненты двоичного вектора). Используя указанное правило, будем иметь
(компоненты вектора) можно с помощью правила перевода целых десятичных чисел в двоичные. Перевод осуществляется последовательным делением исходного числа (в нашем случае 217) и каждого частного на два. Получаемые при этом остатки (0 или 1), записанные в обратном порядке, дают представление десятичного числа в двоичной системе счисления (в нашем случае компоненты двоичного вектора). Используя указанное правило, будем иметь т.е. V=(1,1,0,1,1,0,0,1).
т.е. V=(1,1,0,1,1,0,0,1). областей. Здесь учитывается и внешняя область.
областей. Здесь учитывается и внешняя область.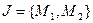 пространство разобьется на 2n=22=4 области. При этом множество
пространство разобьется на 2n=22=4 области. При этом множество  должно быть так построено, чтобы оно имело одну общую область с ранее построенным множеством
должно быть так построено, чтобы оно имело одну общую область с ранее построенным множеством  и пространством J. Результат показан на рис.2.1б. Здесь множество
и пространством J. Результат показан на рис.2.1б. Здесь множество  и одну общую область с пространством J – область
и одну общую область с пространством J – область  . Области записываются в виде конституант, т.к. каждая из построенных областей является пересечением n=2 множеств, т.е. является конституантой.
. Области записываются в виде конституант, т.к. каждая из построенных областей является пересечением n=2 множеств, т.е. является конституантой. должно быть так построено, чтобы оно имело только одну общую область с каждой из ранее построенных областей:
должно быть так построено, чтобы оно имело только одну общую область с каждой из ранее построенных областей: 

 и
и  . Результат изображен на рис.2.1в. Тем самым построены символы Венна для n=1, n=2 и n=3. Аналогично строятся символы Венна и для других значений n.
. Результат изображен на рис.2.1в. Тем самым построены символы Венна для n=1, n=2 и n=3. Аналогично строятся символы Венна и для других значений n.

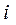 . Отсчет разрядов вектора ведется справа налево, причем крайний правый разряд считается нулевым разрядом. Тогда нулевому разряду вектора V будет соответствовать область (двоичный вектор W0) с десятичным эквивалентом, равным нулю. Согласно формуле (2.1) будем иметь:
. Отсчет разрядов вектора ведется справа налево, причем крайний правый разряд считается нулевым разрядом. Тогда нулевому разряду вектора V будет соответствовать область (двоичный вектор W0) с десятичным эквивалентом, равным нулю. Согласно формуле (2.1) будем иметь:
 , которые ищутся также как и коэффициенты
, которые ищутся также как и коэффициенты  ) означает включение в пересечение (конституанту)
) означает включение в пересечение (конституанту)  множества
множества  , получаем, что вектору W0 соответствует область (конституанта)
, получаем, что вектору W0 соответствует область (конституанта)  . Рассматривая аналогично другие разряды двоичного вектора V и учитывая, что компонента 1 (
. Рассматривая аналогично другие разряды двоичного вектора V и учитывая, что компонента 1 ( ) означает включение в пересечение
) означает включение в пересечение 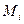 , определим все восемь областей (конституант):
, определим все восемь областей (конституант):




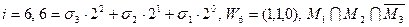
 .
.