
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задать множество M двоичным вектором и аналитическим выражением.
5. Множество M задано двоичным вектором V = (10011110). Задать множество M десятичным эквивалентом и диаграммой Венна. МИНИМИЗАЦИЯ ПРЕДСТАВЛЕНИЯ МНОЖЕСТВА Часто при решении той или иной задачи необходимо упростить или преобразовать к удобному виду различные выражения, содержащие множества. Методы минимизации (упрощения) множества: 1. Применение законов и свойств операций над множествами (тождественные преобразования). 2. Графический метод (круги Эйлера) Метод Квайна. Существуют и другие методы минимизации. Запишем дополнительные законы операций над множествами, которые часто используются в тождественных преобразованиях: Законы склеивания
Законы поглощения
Под сложностью представления множества M понимают число символов Пример 1. Упростить выражение
Используя законы и свойства операций над множествами, получим следующее выражение
Здесь в вертикальных скобках указаны законы и свойства, которые использовались при упрощении. Пример 2. Упростить выражение
Графическим способом. Изобразим с помощью кругов Эйлера пересечение
Рис.3.1 Пример 3. В трехмерном пространстве J = {M1,M2,M3} задано множеством M(M1,M2,M3) десятичным эквивалентом d(M) = 217. Минимизировать множество M методом Квайна. Определить сложность заданного множества и минимизированного множества. В примере 1 п.2 заданное множество M представлено различными способами задания. Воспользуемся некоторыми из них для минимизации заданного множества. Метод Квайна состоит из двух этапов: Определение сокращенной формы множества M (сокращенного множества M). Определение тупиковой формы множества M (минимального множества M). 1 этап. Воспользуемся гиперкубом, построенным для заданного множества в примере 1 п.2 (рис.2.3). Найдем объединение конституант, выраженных двоичными наборами, сопоставленных заштрихованным вершинам гиперкуба, которые соединены ребром, т.е. объединение конституант, отличающихся только в одном разряде:
Здесь в результирующем двоичном наборе прочерк (-) стоит на том месте, на котором в объединяемых двоичных наборах стоят 0 и 1 (рис.3.2).
Рис.3.2
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.217.228 (0.004 с.) |


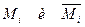 в задающем его выражении.
в задающем его выражении.

 . Данному пересечению соответствует область с наклонной штриховкой (рис.3.1). Теперь изобразим пересечение
. Данному пересечению соответствует область с наклонной штриховкой (рис.3.1). Теперь изобразим пересечение  . Этому пересечению на рис. 3.1 соответствует область с вертикальной штриховкой. Изображаем пересечение
. Этому пересечению на рис. 3.1 соответствует область с вертикальной штриховкой. Изображаем пересечение  . Область с горизонтальной штриховкой соответствует этому пересечению (рис.3.1). Объединяя полученные области, получаем, что
. Область с горизонтальной штриховкой соответствует этому пересечению (рис.3.1). Объединяя полученные области, получаем, что  Это хорошо видно из рис.3.1.
Это хорошо видно из рис.3.1.





