
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таким образом, алгебра a является группой по умножению. И окончательно, Т. К. Выполняется закон коммутативности, алгебраСодержание книги
Поиск на нашем сайте
A = <M,x> является абелевой группой по умножению, нейтральным элементом является e = c, обратными элементами являются: a-1 = b, b-1 = a. Пример 3. Указать тип алгебры, которую образует множество натуральных чисел с заданной в нем операцией сложения. Нам задан аддитивный группоид A = <N,+> и необходимо уточнить его тип. В множестве натуральных чисел N справедлив коммутативный закон сложения:
Значит, заданный группоид является абелевым. В множестве N выполняется ассоциативный закон сложения:
Отсюда следует, что абелев группоид является абелевой полугруппой. Множество натуральных чисел не имеет нейтрального элемента относительно операции сложения, а значит, и обратных элементов. Таким образом, заданный аддитивный группоид A = <N,+> является абелевой полугруппой по сложению. Пример 4. К какому типу относится алгебра A = <Z, В множестве целых чисел выполняются коммутативный и ассоциативный законы умножения. Значит, заданный мультипликативный группоид является абелевой полугруппой по умножению. Нейтральным элементом e является 1, т.е. e=1, т.к.
Для т.к. Таким образом, заданная алгебра является абелевой группой по умножению. Пример 5. Задана алгебра A = <M, +, x>, в которой M={ a,b,c}, а операции: аддитивная (+) и мультипликативная (x) заданы таблицами Кэли:
Показать, что M с заданными в нем операциями образует кольцо. Из определения кольца следует, что алгебра должна быть по сложению абелевой группой. Проверим это. Распишем таблицу Кэли, соответствующую операции (+): a + a = b, b + a = c, c + a = a, a + b = c, b + b = a, c + b = b, a + c = a, b + c = b, c + c = c. Проверяем выполнение условия ассоциативности: (a + b)+c = c + c = c, a+(b + c) = a + b =c, т.е. (a + b)+c = a+(b + c), (a + c)+b = a + b = c, a+(c + b) = a + b =c, т.е. (a + c)+b = a+(c + b), (b + a)+c = c + c = c, b+(a + c) = b + a =c, т.е. (b + a)+c = b+(a + c), (b + c)+a = b + a = c, b+(c + a) = b + a =c, т.е. (b + c)+a = b+(c + a), (c + a)+b = a + b = c, c+(a + b) = c + c =c, т.е. (c + a)+b = c+(a + b), (c + b)+a = b + a = c, c+(b + a) = c + c =c, т.е. (c + b)+a = c+(b + a), и т. д. Закон ассоциативности выполняется, значит, заданная алгебра является полугруппой по сложению. Так как a + c=c + a=a, b + c=c + b=b, c + c = c, то элемент c является нейтральным элементом относительно операции сложения, т.е. e=c. Операция (+) является аддитивной, следовательно, c является нулем. Тогда обратными элементами элементов a, b будут: -a = b, -b = a, т. к. a + b = b + a = c и b + a = a + b = c. Так как в полугруппе выполнима обратная операция, то она является группой. Проверим свойство коммутативности: a + b=c=b + a, a + c=a=c + a, b + c=b=c + b, т.е. указанное свойство выполняется.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.163.138 (0.007 с.) |

 m,n
m,n  N m+n = n+m.
N m+n = n+m.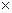 >, являющаяся совокупностью множества целых чисел с заданной в нем операцией умножения.
>, являющаяся совокупностью множества целых чисел с заданной в нем операцией умножения.






