
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следовательно, группа является абелевой.Содержание книги
Поиск на нашем сайте
Заданная алгебра по умножению является мультипликативным группоидом. Для того, чтобы алгебра A = <M, +, x> была кольцом, осталось показать, что умножение связано со сложением законами дистрибутивности:
Для проверки выполнения этих законов распишем таблицу Кэли, соответствующую операции (x):
и воспользуемся разложением таблицей Кэли, соответствующей операции (+):
Законы дистрибутивности выполняются. Следовательно, заданная алгебра A = <M, +, x> является кольцом. Под алгеброй множеств (алгеброй Кантора, булевой алгеброй множеств) понимают алгебру вида
где булеан Для операций алгебры множеств выполняются следующие законы и свойства: Коммутативность объединения и пересечения
Ассоциативности объединения и пересечения
Дистрибутивности пересечения относительно объединения и объединения относительно пересечения
Идемпотентности объединения и пересечения
5. Действия с универсальным J и пустым
Де Моргана
Двойного дополнения
Алгебра множеств по аддитивной операции объединения и мультипликативной операции пересечения является абелевой полугруппой. Любая теорема алгебры множеств и, в частности свойства операций над множествами выводятся из первых трех законов и свойств:
Которые в свою очередь доказываются только в терминах отношения принадлежности. Пример 6. Доказать закон
Для доказательства данного закона используем отношение принадлежности. Пусть Если Если Тем самым доказано, что
Пусть
В соответствии с определением равенства множеств приходим к требуемому закону
Пример 7. Доказать, что
Данное соотношение доказывается следующими преобразованиями:
Здесь в вертикальных скобках указаны свойства и законы, которые использовались при доказательстве. Для доказательства законов и других теоретико-множественных соотношений часто используют круги Эйлера. Пример 8. Доказать закон
С помощью кругов Эйлера.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.72.44 (0.006 с.) |






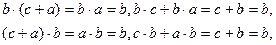


 ,
, – носитель алгебры, а сигнатура – операции объединения
– носитель алгебры, а сигнатура – операции объединения  , пересечения
, пересечения  и дополнения
и дополнения  .
. ,
, 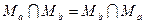 .
. ,
, .
. ,
,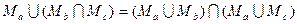 .
.
 множествами
множествами
 ,
,  .
. .
. ,
, , тогда, согласно определению объединения множеств,
, тогда, согласно определению объединения множеств, 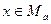 или
или  .
. с любым множеством, т.е.
с любым множеством, т.е.  и
и  , следовательно, по определению пересечения множеств
, следовательно, по определению пересечения множеств  .
. и
и  по определению пересечения множеств, следовательно,
по определению пересечения множеств, следовательно, 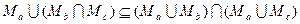 .
. , то
, то  с любым множеством, т.е.
с любым множеством, т.е. 
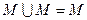 .
.




