
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Северодонецкий технологический институтСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ ВОСТОЧНОУКРАИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СЕВЕРОДОНЕЦКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ «ДИСКРЕТНАЯ МАТЕМАТИКА» (ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ, ЧАСТЬ 11) СЕВЕРОДОНЕЦК 1997 МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ ВОСТОЧНОУКРАИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СЕВЕРОДОНЕЦКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ «ДИСКРЕТНАЯ МАТЕМАТИКА» (ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ, ЧАСТЬ 11) для студентов всех форм обучения специальностей «Компьютерные интеллектуальные системы и сети», «Технология проблемного и системного программирования» Утверждено Кафедрой ПМ Протокол № 29 От 12.02.97 Северодонецк СТИ 1997 Методические указания к практическим занятиям по курсу «Дискретная математика» (Элементы теории множеств, часть 11) для студентов всех форм обучения специальностей «Компьютерные интеллектуальные системы и сети», «Технология проблемного и системного программирования»/ Сост. А.Е.Богданов.- Северодонецк: СТИ, 1997.- 35 с. Составитель А.Е.Богданов Данные методические указания содержат темы, не вошедшие в первую часть одноименных методических указаний. Рассматриваемые темы позволят студентам успешно продолжить изучение последующих разделов дискретной математики. В нашем случае указанное условие выполняется только для элемента c Рассмотрим условие коммутативности:
Имеем: a + b = c = b + a, a + c b + c = b =c +b. Так как a + c Проверим свойство ассоциативности:
В нашем случае: (a + b)+c=c + c=c, a+(b + c)=a + b=c, т.е. (a + b)+c = a+(b + c), (a + c)+b=a + b=c, a+(c + b)=a + b=c, т.е. (a + c)+b = a+(c + b), (b + a)+c=c + c=c, b+(a + c)=b+ a=c, т.е. (b + a)+c = b+(a + c), (b + c)+a=b + a=c, b+(c + a)=b + b=c, т.е. (b + c)+a = b+(c + a), (c + a)+b=b + b=c, c+(a + b)=c + c=c, т.е. (c + a)+b = c+(a + b), (c + b)+a=b + a=c, c+(b + a)=c + c=c, т.е. (c + b)+a = c+(b + a), (a + a)+b=b + b=c, a+(a + b)=a + c=a, т.е. (a + a)+b
Не является ассоциативным или полугруппой. По определению элемент e
Указанное условие для элементов множества M не выполняется. Поэтому заданный группоид A не имеет нейтрального элемента. Этим элементом мог бы быть элемент c, т.к. b + c = c + b = b, c + c = c, но он не удовлетворяет элементу a множества M, a + c = a, а c + a = b. Так как группоид A не имеет нейтрального элемента, то он не имеет и обратных элементов. Имеем единственный результат: аддитивный группоид A = <M, + >. Пример 2. В трехэлементном множестве M = {a,b,c} мультипликативная операция задана таблицей Кэли
Распишем таблицу Кэли
Так как Так как Рассмотрим свойство ассоциативности:
и т. д. Так как
Тогда обратным элементом a-1 элементу a будет b, т.е. a-1 = b, т.к. b-1 = a, т.к. Де Моргана
Двойного дополнения
Тем самым доказано, что
Пусть
С помощью кругов Эйлера.
Рис.1.1 Показать, что M с заданными в нем операциями образует коммутативное тело. Для элементов из M определить нейтральные и обратные элементы относительно заданных операций. Заменить элементы a, b, c соответственно на числа 1,2,3 и истолкуйте заданные операции в числовом множестве. Доказать закон де Моргана
Доказать закон де Моргана
С помощью кругов Эйлера. Доказать, что
СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВА Множество M при фиксированных независимых подмножествах
где называется первичным термом, а
называется конституантой. Пояснение. Каждое фиксированное множество
Множество M можно задать в виде двоичной таблицы, каждой строке которой взаимно однозначно соответствует конституанта. Множество строк таблицы линейно упорядочено по возрастанию десятичного эквивалента соответствующего двоичного набора. Столбцам соответствуют множества, образующие пространство, последний столбец сопоставляется множеству M, и единица указывает на вхождение соответствующей конституанты в множество M. Пример 1. В трехмерном пространстве 1. Для представления заданного множества M в виде двоичного вектора воспользуемся формулой (2.2), где коэффициент Так как
Теперь необходимо подобрать коэффициенты 217 = 1.27+1.26+0.25+1.24+1.23+0.22+0.21+1.20. Множество найденных коэффициентов и является двоичным вектором, т.е. V=(1,1,0,1,1,0,0,1). Определить коэффициенты
2. Построение диаграммы Венна начинается с разбиения пространства J на 2n областей с помощью n фигур (замкнутых линий), где n – число различных множеств, входящих в J. При этом каждая последующая фигура должна иметь одну и только одну общую область с каждой из ранее построенных фигур. Такое разбиение называют символом Венна. По условию задачи При n=1 пространство разбивается на две области (рис.2.1а). При этом общей областью пространства J и множества M является само множество M. При n=2, т.е. При n=3, т.е.
Каждой из областей (конституант) можно сопоставить двоичный вектор W длины n, который представим в виде десятичного эквивалента d(c) по формуле (2.1). С другой стороны,
Определяя коэффициенты 0 = 0.22 + 0.21 + 0.20. Тем самым мы определили двоичный вектор W0 = (0,0,0), соответствующий рассматриваемой области. Учитывая, что компонента 0 (
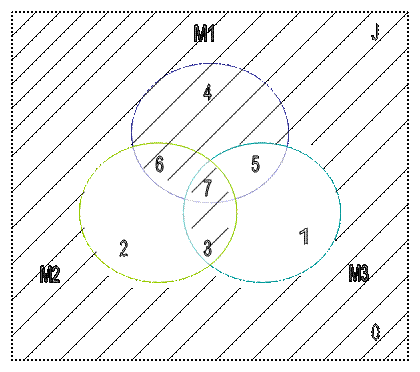
Тогда, учитывая, что единица в двоичном векторе V означает включение соответствующей области в множество M, а нуль – исключение, построим диаграмму Венна. Заданное (отмечено штриховкой) множество M изображено на рис.2.2.
Рис.2.2 Рис.2.4 1. Те области (конституанты), которые входят в заданное множество M, отмечены штриховкой. Номер каждой области в символе Венна соответствует десятичному эквиваленту этой области. Штриховка области означает, что конституанта, соответствующая десятичному эквиваленту заштрихованной области, входит в множество M. Поэтому в таблице в столбце M на соответствующем месте будет стоять единица. Учитывая это, можно построить таблицу:
2. Двоичный вектор V, соответствующий заданному множеству M, есть столбец M в построенной таблице, записанный в виде V = (1,0,0,1,1,0,1,0). Рис.2.5 5. Используя, например, гиперкуб, запишем заданное множество M как объединение конституант
ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Рис.2.6 Рис.2.7 Метод Квайна. Законы склеивания
Законы поглощения
Под сложностью представления множества M понимают число символов Пример 1. Упростить выражение
Графическим способом. Изобразим с помощью кругов Эйлера пересечение
Рис.3.1 Пример 3. В трехмерном пространстве J = {M1,M2,M3} задано множеством M(M1,M2,M3) десятичным эквивалентом d(M) = 217. Минимизировать множество M методом Квайна. Определить сложность заданного множества и минимизированного множества. В примере 1 п.2 заданное множество M представлено различными способами задания. Воспользуемся некоторыми из них для минимизации заданного множества. Метод Квайна состоит из двух этапов: Рис.3.2 Каждая конституанта строки после подстановки вместо прочерка нуля сравнивалась с конституантами столбцов. Если существует столбец с такой же конституантой, то на пересечении рассматриваемых строки и столбца ставилась единица. После этого в той же конституанте строки вместо прочерка ставилась единица и проводилась аналогичная процедура сравнения. Рис.3.3 1. Найдем M сокр. Для этого определим объединение конституант, соответствующих соединенным ребрам заштрихованным вершинам гиперкуба:
Таким образом,
Сложности множеств M и M min равны:
Примеры для самостоятельной работы Упростить выражение
Упростить соотношение
Графическим методом. Упростить выражение
С помощью кругов Эйлера. Упростить выражение
Упростить выражение
7. В трехмерном пространстве J = {M1,M2,M3} множество M(M1,M2,M3) задано двоичным вектором V = (1,0,0,1,1,1,1,1). Минимизировать данное множество M методом Квайна. Определить сложность заданного множества и минимизированного множества. 8. В трехмерном пространстве J = {M1,M2,M3} задано множество M(M1,M2,M3) диаграммой Венна (рис.3.4)
Рис.3.4 СПИСОК ЛИТЕРАТУРЫ СОДЕРЖАНИЕ 1. Понятие алгебры. Алгебра множеств 2. Способы задания множеств 3. Минимизация представления множеств Учебное издание МЕТОДИЧЕСКИЕ УКАЗАНИЯ МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ ВОСТОЧНОУКРАИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СЕВЕРОДОНЕЦКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.156.180 (0.013 с.) |

 M: c + c = c. Для элементов a,b
M: c + c = c. Для элементов a,b  M условие идемпотентности не выполняется: a + a = b, b + b = c. Значит, заданный группоид не является идемпотентным.
M условие идемпотентности не выполняется: a + a = b, b + b = c. Значит, заданный группоид не является идемпотентным. m,n
m,n  M mfn = nfm.
M mfn = nfm. c + a (a + c = a, c + a = b),
c + a (a + c = a, c + a = b), c + a, то группоид A = <M, + > не является коммутативным.
c + a, то группоид A = <M, + > не является коммутативным. a+(a + b). Условие ассоциативности не выполняется. Значит, группоид A = <M, + >
a+(a + b). Условие ассоциативности не выполняется. Значит, группоид A = <M, + > M является нейтральным, если
M является нейтральным, если

 = b,
= b,  = c,
= c,  = a,
= a, = c,
= c,  = a,
= a, 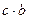 = b,
= b, = a,
= a,  = b,
= b,  = c.
= c.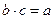 , то группоид не является идемпотентным.
, то группоид не является идемпотентным. то группоид обладает свойством коммутативности, т.е. он является коммутативным или абелевым группоидом.
то группоид обладает свойством коммутативности, т.е. он является коммутативным или абелевым группоидом.
 то нейтральный элемент e существует: e=c. Группоид A = <M,x> мультипликативный, поэтому нейтральный элемент c является единицей.
то нейтральный элемент e существует: e=c. Группоид A = <M,x> мультипликативный, поэтому нейтральный элемент c является единицей. а обратным элементу b будет a, т.е.
а обратным элементу b будет a, т.е.
 ,
,  .
. .
.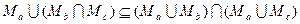 .
. , тогда
, тогда  и
и  . Если
. Если 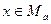 , то x принадлежит объединению
, то x принадлежит объединению  с любым множеством, т.е.
с любым множеством, т.е.  .Если
.Если  , то
, то  и
и  . Это означает по определению пересечения множеств, что
. Это означает по определению пересечения множеств, что  . Тогда x принадлежит объединению
. Тогда x принадлежит объединению  с любым множеством, т.е.
с любым множеством, т.е. 
 .
. универсального множества J, т.е.
универсального множества J, т.е.  можно задать в виде объединения конституант
можно задать в виде объединения конституант ,
,



 ,
, 
 разбивает пространство J на две части: на собственно
разбивает пространство J на две части: на собственно 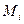 и на
и на  . При независимых множествах
. При независимых множествах  пространственно разбивается на
пространственно разбивается на  =
=  областей. Каждая область является пересечением n множеств
областей. Каждая область является пересечением n множеств  . Этой области можно сопоставить двоичный вектор
. Этой области можно сопоставить двоичный вектор  , в котором
, в котором  , если в конституанту
, если в конституанту  входит
входит  , если входит
, если входит  . (2.1)
. (2.1) множество
множество  задано десятичным эквивалентом d(M)=217. Задать множество M: 1. двоичным вектором, 2. диаграммой Венна, 3. таблицей, 4. гиперкубом, 5. аналитическим выражением.
задано десятичным эквивалентом d(M)=217. Задать множество M: 1. двоичным вектором, 2. диаграммой Венна, 3. таблицей, 4. гиперкубом, 5. аналитическим выражением. принимает значение 0 или 1, 2n – длина двоичного вектора (число разрядом), n – число множеств в пространстве J.
принимает значение 0 или 1, 2n – длина двоичного вектора (число разрядом), n – число множеств в пространстве J. . Тогда
. Тогда
 принимающие значение 0 или 1, такие, что сумма в правой части записанного выражения была равна 217. В результате мы получим
принимающие значение 0 или 1, такие, что сумма в правой части записанного выражения была равна 217. В результате мы получим
 т.е. V=(1,1,0,1,1,0,0,1).
т.е. V=(1,1,0,1,1,0,0,1). областей. Здесь учитывается и внешняя область.
областей. Здесь учитывается и внешняя область.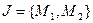 пространство разобьется на 2n=22=4 области. При этом множество
пространство разобьется на 2n=22=4 области. При этом множество  должно быть так построено, чтобы оно имело одну общую область с ранее построенным множеством
должно быть так построено, чтобы оно имело одну общую область с ранее построенным множеством  и пространством J. Результат показан на рис.2.1б. Здесь множество
и пространством J. Результат показан на рис.2.1б. Здесь множество  и одну общую область с пространством J – область
и одну общую область с пространством J – область  . Области записываются в виде конституант, т.к. каждая из построенных областей является пересечением n=2 множеств, т.е. является конституантой.
. Области записываются в виде конституант, т.к. каждая из построенных областей является пересечением n=2 множеств, т.е. является конституантой. должно быть так построено, чтобы оно имело только одну общую область с каждой из ранее построенных областей:
должно быть так построено, чтобы оно имело только одну общую область с каждой из ранее построенных областей: 

 и
и  . Результат изображен на рис.2.1в. Тем самым построены символы Венна для n=1, n=2 и n=3. Аналогично строятся символы Венна и для других значений n.
. Результат изображен на рис.2.1в. Тем самым построены символы Венна для n=1, n=2 и n=3. Аналогично строятся символы Венна и для других значений n.

 разряду двоичного вектора V соответствует область с десятичным эквивалентом, равным
разряду двоичного вектора V соответствует область с десятичным эквивалентом, равным 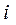 . Отсчет разрядов вектора ведется справа налево, причем крайний правый разряд считается нулевым разрядом. Тогда нулевому разряду вектора V будет соответствовать область (двоичный вектор W0) с десятичным эквивалентом, равным нулю. Согласно формуле (2.1) будем иметь:
. Отсчет разрядов вектора ведется справа налево, причем крайний правый разряд считается нулевым разрядом. Тогда нулевому разряду вектора V будет соответствовать область (двоичный вектор W0) с десятичным эквивалентом, равным нулю. Согласно формуле (2.1) будем иметь:
 , которые ищутся также как и коэффициенты
, которые ищутся также как и коэффициенты  множества
множества  . Рассматривая аналогично другие разряды двоичного вектора V и учитывая, что компонента 1 (
. Рассматривая аналогично другие разряды двоичного вектора V и учитывая, что компонента 1 (




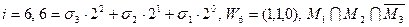
 .
.



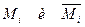 в задающем его выражении.
в задающем его выражении.
 . Данному пересечению соответствует область с наклонной штриховкой (рис.3.1). Теперь изобразим пересечение
. Данному пересечению соответствует область с наклонной штриховкой (рис.3.1). Теперь изобразим пересечение  . Этому пересечению на рис. 3.1 соответствует область с вертикальной штриховкой. Изображаем пересечение
. Этому пересечению на рис. 3.1 соответствует область с вертикальной штриховкой. Изображаем пересечение  . Область с горизонтальной штриховкой соответствует этому пересечению (рис.3.1). Объединяя полученные области, получаем, что
. Область с горизонтальной штриховкой соответствует этому пересечению (рис.3.1). Объединяя полученные области, получаем, что  Это хорошо видно из рис.3.1.
Это хорошо видно из рис.3.1.


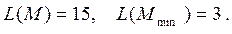



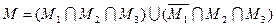
 .
.
 3
3 15
15 26
26


