Изображение окружности на комплексном чертеже

Рассмотрим три случая.

1. Окружность 1 лежит в плоскости уровня g (рис,7.7.) В этом случае она проецируется на одну из плоскостей проекций в натуральную величину, а на другой плоскости совпадает со следом плоскости g_V.

g½½H 1¢- натуральная величина l² = g_V.

2. Окружность 1 лежит в проецирующей плоскости a (рис,7,8.). Одна из ее проекций совпадает со следом плоскости, a_V вторая проекция эллипс.

lÌa, l² = a_V; А¢В¢ - большая ось эллипса А¢В¢ = 2R, C¢D¢ - малая ось.

3. Окружность 1 лежит в плоскости общего положения (рис.7.9.) проецируется на обе плоскости в эллипсы.

Большие оси эллипсов l¢, l² принадлежат линиям уровня, соответственно горизонтали и фронтали, и по длине равны диаметру окружности 1. Поэтому большую ось А¢В¢ эллипса l¢ на Н откладываем на горизонтальной проекции h¢ горизонтали, большую ось М²N² эллипса l² - на фронтальной проекции f² фронтали.

А², В², М¢, N¢ находим по условию принадлежности их горизонтали м фронтали. Малые оси эллипсов принадлежат линиям наибольшего наклона. Для построения малых осей C¢D¢ и Р²Q² проводим n¢^А¢В¢ и m²^M²N².

 

7.4. Винтовые линии

Наиболее часто встречающаяся в инженерной практике пространственная кривая - это цилиндрическая винтовая линия. (Рис.7.10.)

Цилиндрическая винтовая линия представляет собой траекторию точки, которая совершает равномерное поступательное движение вдоль оси равномерного вращающегося цилиндра. Ось цилиндра будет осью винтовой линии, а радиус его - радиусом винтовой линии. Расстояние Р., на которое точка перемещается вдоль оси цилиндра за один его оборот, называется шагом винтовой линии.

Для построения проекции винтовой линии предварительно строим проекции прямого кругового цилиндра (рис.7,11). Окружность основания цилиндра (горизонтальная проекция) и шаг (фронтальная проекция) делит на одинаковое число равных частей. Из точек деления окружности проводим линии связи, а через соответствующие точки деления шага горизонтальные прямые.

Отмечаем точки 1², 2², 3²... 8², в которых пересекаются соответственные прямые. Соединив, их плавной кривой, получим фронтальную проекцию винтовой линии.

	Рис.7.10.
		Рис.7.11.

Различают правую и левую винтовые линии.

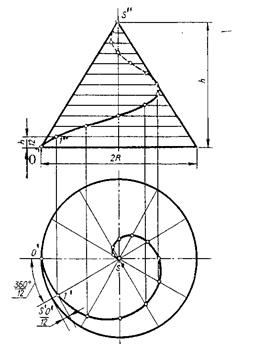
Если наблюдатель смотрит вдоль винтовой линии и видит ее при подъеме закручивающейся против часовой стрелки, то винтовая линия называется правой.

Если точка перемещается равномерно по обра-зующей прямого кругового конуса, а образующая совершает вращательное движение вокруг оси конуса с постоянной скоростью, то траекторией точки является коническая винтовая линия.

	Рис.7.12.

ПОВЕРХНОСТИ

Поверхности - это бесконечное разнообразие геометрических фигур. Любой предмет в природе или в технике ограничивается своей поверхностью. Инженерная деятельность связана непосредственно с конструированием, расчетом, изготовлением различных технических поверхностей.

8.1. Способы образования и задания поверхностей,