Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кривые линии и их проекционные свойства.Содержание книги
Поиск на нашем сайте
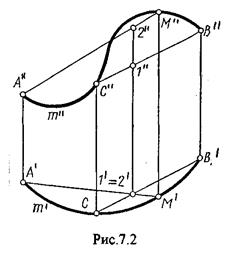
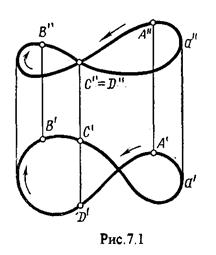
7.1. Основные понятия и определения Кривую линию можно представить как траекторию точки, перемещающейся в пространстве или на плоскости, Кривая линия так же может быть получена в результате пересечения поверхности с плоскостью или двух поверхностей между собой, Кривые линии могут быть плоские, т.е. такие, все точки которых принадлежат одной плоскости и пространственные, точки которых не принадлежат одной плоскости. Примерами плоских кривых являются: окружность, эллипс, парабола. Примером пространственной кривой является винтовая линия, Линия считается закономерной, если в своем образовании она подчинена какому - нибудь закону. Если, при этом, кривая в декартовой системе координат определяется алгебраическим уравнением, то она называется алгебраической. Примерами алгебраических кривых являются окружность, эллипс, парабола, гипербола. Степень уравнения кривой определяет порядок кривой. Кривая линия определяется положениями составляющих ее точек, Точки кривой определяются их координатами. На чертеже кривая задается своими проекциями. Для построения ортогональных проекций кривой (пространственной или плоской) необходимо построить проекции ряда точек, принадлежащих этой кривой, и соединить их между собой в той же последовательности, в какой они располагались на оригинале, При задании кривой ее проекциями необходимо указать, по крайней мере, проекции одной точки, принадлежащей кривой (рис.7.1.). По чертежу кривой в общем случае можно без дополнительных построений определить пространственная она или плоская. На рис.7.1. кривая а пространственная, т.к. она имеет конкурирующие точки С, D. Если по чертежу не понятно, плоская кривая или пространственная, требуются дополнительные построения. На кривой нужно выбрать три произвольные точки и проверить, лежит ли любая четвертая точка кривой в плоскости, определяемой первыми тремя. Кривая m, изображенная на рис.7.2. пространственная, т.к. точка М(М¢, М²) не лежит в плоскости a заданной точками А, В, С этой кривой.
Плоских кривых Если точка А принадлежит кривой m, то проекция этой точки А¢ принадлежит проекции m¢ кривой. Секущая и касательная к кривой проецируются соответственно в секущую и касательную к проекции кривой. Пусть через точку А кривой m проведена секущая n (рис.7.3.).
Проекции плоских кривых Чтобы наиболее точно передать форму кривой линии, при построении ее проекций необходимо, прежде всего, отложить характерные точки. Такими точками являются особые точки кривой, а так же точки наиболее удаленные от плоскостей проекций и наиболее близкие к ним. Точка кривой называется обыкновенной, если в этой точке к кривой можно провести единственную касательную. На рис.7.4. такой точкой является точка М.
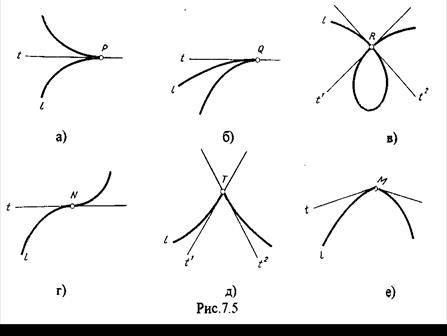
 Другие точки называют особыми (точки А, В). К ним относятся точки возврата (рис.7.5,а,б.), точки самопересечения (рис.7.5,в.), точки перегиба (рис.7,5,г.), точки излома (рис.7.5,д,е.).Особым точкам плоской кривой соответствуют такие же точки на ее проекции. Кривая, состоящая только из обыкновенных точек, называется плавной кривой. Другие точки называют особыми (точки А, В). К ним относятся точки возврата (рис.7.5,а,б.), точки самопересечения (рис.7.5,в.), точки перегиба (рис.7,5,г.), точки излома (рис.7.5,д,е.).Особым точкам плоской кривой соответствуют такие же точки на ее проекции. Кривая, состоящая только из обыкновенных точек, называется плавной кривой.
На рис.7.6. выполнено построение горизонтальной проекции l¢ кривой линии 1, принадлежащей плоскости a(h,f) по заданной фронтальной 1². Точки А, К, N, D, Е - характерные. А - точка, наиболее удаленная от горизонтальной плоскости проекции, К - точка, наиболее удаленная от фронтальной плоскости проекций, Е - самая низкая, D - точка возврата, N - точка прекращения. Точки В, С - промежуточные. Все точки кривой строятся по условию принадлежности их плоскости.
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.77.51 (0.007 с.) |

 7.2. Некоторые свойства проекций пространственных и
7.2. Некоторые свойства проекций пространственных и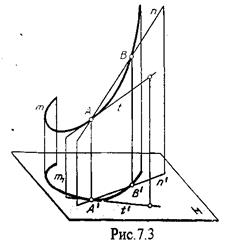 Проекция секущей определяется точками А¢ и В¢ принадлежащими проекции m¢ рассматриваемой кривой. Прямая n¢, пересекающая проекцию кривой, является по отношению к m¢ секущей. Касательную t можно рассматривать как предельное положение секущей, которое занимает последняя при сближении точек пересечения А и В в одну точку, В этом случае совпадут друг с другом и их проекции, т.е. проекция n¢ секущей превратиться в касательную t¢ к проекции m кривой.
Проекция секущей определяется точками А¢ и В¢ принадлежащими проекции m¢ рассматриваемой кривой. Прямая n¢, пересекающая проекцию кривой, является по отношению к m¢ секущей. Касательную t можно рассматривать как предельное положение секущей, которое занимает последняя при сближении точек пересечения А и В в одну точку, В этом случае совпадут друг с другом и их проекции, т.е. проекция n¢ секущей превратиться в касательную t¢ к проекции m кривой.