Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неоднородное уравнение теплопроводности со смешанными граничными условиями.
Рассмотрим решение уравнения на примере следующей задачи. В конечном стержне Эта задача сводиться к решению уравнения
с начальным условием Решение ищем в виде суммы Тогда функция
с однородным начальным условием К решению соответствующего однородного уравнения
Окончательное решение примет вид
Примеры: 1. Решить уравнение с начальным условием и граничными условиями 2. Решить уравнение с начальным условием и граничными условиями 3. Решить уравнение с начальным условием и граничными условиями Указание: решение следует искать в виде 4. Решить уравнение с начальным условием и граничными условиями Указание: решение следует искать в виде Лекция 17. Тема: Уравнение Лапласа. Простейшим уравнением эллиптического типа является уравнение Лапласа
В случае функции u=u(x,t) двух независимых переменных х, у уравнение Лапласа имеет вид
и в случае функции одного аргумента имеем
Решениями уравнения (3) являются функции Определение: Функция Фундаментальные решения уравнений Лапласа. Оператор Лапласа (1) в цилиндрических координатах
в сферических координатах
Пользуясь сферическими координатами, видим, что решение u=u(r) определяется из ОДУ
Интегрируя это уравнение, находим
Полагая, например, с1=1, с2=0, получаем
которую называют фундаментальным решением уравнения Лапласа в пространстве.
Пользуясь цилиндрическими координатами, находим, что решение u=u(r) определяется из ОДУ
интегрируя которое, получим
Выбирая с1=-1, с2=0, получаем
которую называют фундаментальным решением уравнения Лапласа на плоскости. Формулы Грина.
- первая формула Грина. Меняя в формуле (4) u и v местами, получим
Вычитая равенства (4) и (5) почленно, находим
Это – вторая формула Грина. Наконец, полагая в (4) u=v, получим
Это – третья формула Грина. Здесь всюду n – вектор внешней нормали к гладкой или кусочно-гладкой замкнутой поверхности Основная интегральная формула Грина. Для уравнения Лапласа на плоскости фундаментальное решение имеет вид
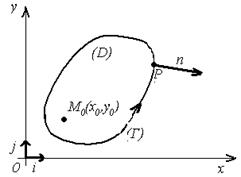
Здесь Г – граница области D, n – вектор внешней нормали к границе (рис. 1). Таким образом, всякая гармоническая в области D функция u(x,y) есть сумма двух потенциалов
логарифмического потенциала простого слоя и логарифмического потенциала двойного слоя соответственно.
Рис. 1. Лекция 18.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.106.232 (0.008 с.) |
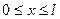 с теплоизолированной поверхностью действует источник тепла по закону
с теплоизолированной поверхностью действует источник тепла по закону 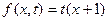 . На левом конце задан тепловой поток
. На левом конце задан тепловой поток  , температура правого конца изменяется по закону
, температура правого конца изменяется по закону 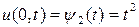 . Начальная температура
. Начальная температура 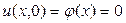 . Найти закон изменения температуры при a=1.
. Найти закон изменения температуры при a=1.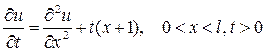
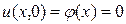 и граничными условиями
и граничными условиями  ,
,  .
.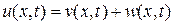 . Подберем одну из функций, удовлетворяющую граничным условиям. Например, пусть
. Подберем одну из функций, удовлетворяющую граничным условиям. Например, пусть 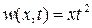 . Очевидно, что
. Очевидно, что  . Метод Фурье не определяет функцию w(x,t), она подбирается.
. Метод Фурье не определяет функцию w(x,t), она подбирается.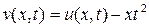 удовлетворяет уравнению
удовлетворяет уравнению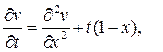
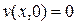 и однородными граничными условиями
и однородными граничными условиями 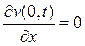 ,
,  .
.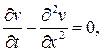 применим метод разделения переменных
применим метод разделения переменных  . В результате получим собственные значения
. В результате получим собственные значения  и соответствующие собственные функции
и соответствующие собственные функции  . Подставив v(x,t) в уравнение по известной схеме, получим
. Подставив v(x,t) в уравнение по известной схеме, получим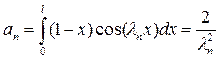
 ,
, .
.
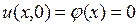
 ,
,  .
.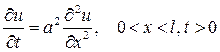
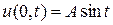 ,
, 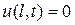 .
.
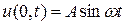 ,
,  , где v(x,t) – решение уравнения
, где v(x,t) – решение уравнения 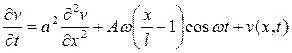 с начальным условием
с начальным условием  и граничными условиями
и граничными условиями 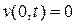 ,
, 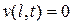 .
.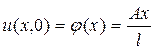
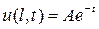 .
. .
.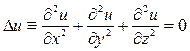 (1)
(1)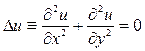 (2)
(2) . (3)
. (3) , где с1, с2 – произвольные постоянные.
, где с1, с2 – произвольные постоянные. называется гармонической в области
называется гармонической в области  , если
, если 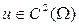 и удовлетворяет в области
и удовлетворяет в области  уравнению Лапласа (1).
уравнению Лапласа (1). определяется как
определяется как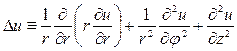
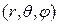
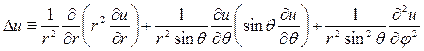
 .
.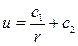 .
.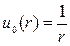 ,
, ,
,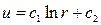 .
.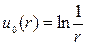 .
. (4)
(4)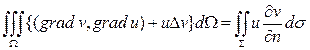 (5)
(5)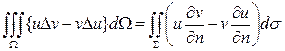 (6)
(6) (7)
(7)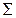 .
. . Можно получить интегральную формулу для гармонической функции двух аргументов:
. Можно получить интегральную формулу для гармонической функции двух аргументов: