Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Единственность решения смешанной задачи.
Теорема: Решение смешанной задачи для вынужденных колебаний струны:
единственно. Доказательство: Допустим, что существуют два решения u1(x,t), u2(x,t) задачи (1) – (3). Тогда разность
нулевым граничным условиям
и нулевым начальным условиям
Покажем, что соотношение (4) – (6) удовлетворяет лишь функция, тождественно равная нулю. Рассмотрим функцию
и покажем, что при условиях (4) – (6) она не зависит от времени t. Взяв производную по t, получаем
так как внеинтегральное слагаемое обращается в нуль в силу условий (5), а Итак,
и, следовательно,
следует, что
откуда
Интеграл (7) можно переписать в виде
Величина
является кинетической энергией струны в момент времени t, а
- ее потенциальная энергия, так что функция E(t) с точностью до постоянного множителя Изложенный метод доказательства единственности решения смешанной задачи называется энергетическим.
Примеры:
1. с начальными условиями и граничными условиями 2. Лекция 12.
Тема: Колебания круглой мембраны. Применение преобразований Лапласа к решению смешанной задачи.
Метод Фурье применяется также при изучении колебаний ограниченных тел, плоских или объемных. Рассмотрим задачу о свободных колебаниях под действием начальных возмущений однородной круглой мембраны радиуса r0 с центром в начале координат, закрепленной по краю. Уравнение колебаний мембраны имеет вид
Введем полярные координаты
запишем уравнение колебаний мембраны в виде:
граничными условиями
(мембрана закреплена по краю) и начальным условиям
Ограничимся важным частным случаем осесемметричных колебаний, когда начальные функции f и F не зависят от
При этом предположении задача сводиться к отысканию решения u=(r,t) уравнения
при граничном условии
и начальных условиях
Применяя метод разделения переменных, будем искать нетривиальные решения уравнения (4), удовлетворяющие граничному условию (5), в виде
Подставляя функцию u(r,t) в форму (7) в уравнение (4) и разделяя переменные, получим
Равенства (8) приводят к двум обыкновенным ДУ
Итак, мы пришли к задаче на собственные значения: найти те значения параметра Запишем уравнение (10) в виде:
Это дифференциальное уравнение Бесселя с
Из условия
граничное условие
откуда следует, что число
где
откуда получаем собственные значения
и соответствующие собственные функции
При
Функция
будет решением уравнения (4), удовлетворяющему граничному условию (5). Решение u(x,r) исходной задачи (4) – (6) ищем в виде формального ряда
где
Если подставив an и bn в (12), ряд сходится равномерно, то мы поучаем решение задачи (4) – (6). Применение преобразований Лапласа к решению смешанной задачи.
Пусть требуется найти решение u(x,t) уравнения
удовлетворяющее начальным условиям
и граничными условиями
Применяя преобразование Лапласа по t, предположим, что
Так как операция дифференцирования по х и операция интегрирования по t в преобразовании Лапласа перестановочны, получим
(здесь величина р рассматривается как параметр, и вместо частных производных пишут обычные). По правилу дифференцирования оригиналов имеем
Отсюда, учитывая начальные условия (2), получаем
Пусть
Переходя к изображениям, сводим задачу (1) – (3) для уравнения с частными производными к граничной задаче для обыкновенного ДУ: найти решение U(x,p) уравнения
при граничных условиях
Пусть U(x,p) - решение задачи (4) – (5). Тогда функция u(x,t) (оригинал для U(x,p))будет решением исходной задачи (1) – (3). Пример: Струна l закреплена на концах x=0, x=l. Начальные отклонения струны определяются формулой Решение: Задача сводиться к решению уравнения
при начальных условиях
и граничных условиях Применим преобразование Лапласа. По правилу дифференцирования с учетом начальных условий получим
Граничные условия дают
Приходим к граничной задаче для ОДУ:
Решая уравнение (*) как линейное с постоянными коэффициентами, найдем
Из условий (**) получаем с1=с2=0, так что
Оригиналом для U(x,p) является функция
которая будет решением для (6) – (8).
Примеры: 1.
Лекция 13.
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.126.80 (0.037 с.) |
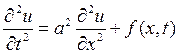 (1)
(1) (2)
(2)
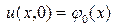 . (3)
. (3)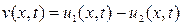 этих решений будет удовлетворять однородному уравнению
этих решений будет удовлетворять однородному уравнению (4)
(4) (5)
(5)
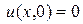 . (6)
. (6) (7)
(7)
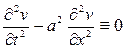 , так как v(x,t) – решение уравнения (4).
, так как v(x,t) – решение уравнения (4). , т.е.
, т.е.  . Учитывая начальные условия (6), получаем
. Учитывая начальные условия (6), получаем ,
, . Из того, что интеграл от непрерывной неотрицательной функции равен нулю,
. Из того, что интеграл от непрерывной неотрицательной функции равен нулю,
 ,
, , так что
, так что  . В силу первого из начальных условий (6)
. В силу первого из начальных условий (6)  , и значит,
, и значит,  , т.е.
, т.е.  .
.
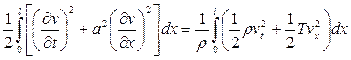


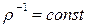 выражает полную энергию.
выражает полную энергию.



 .
. . Тогда отклонение точек мембраны будет функцией полярных координат
. Тогда отклонение точек мембраны будет функцией полярных координат 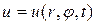 . Пользуясь выражением для оператора Лапласа
. Пользуясь выражением для оператора Лапласа 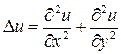 в полярных координатах,
в полярных координатах,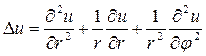 ,
, , (1)
, (1) (2)
(2) (3)
(3) . Ясно, что тогда любой момент времени t>0 величина отклонения мембраны не будет зависеть от полярного угла
. Ясно, что тогда любой момент времени t>0 величина отклонения мембраны не будет зависеть от полярного угла 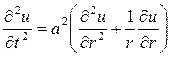 (4)
(4)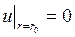 (5)
(5)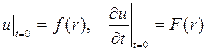 (6)
(6)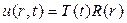 (7)
(7) (8)
(8) , (9)
, (9)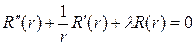 , (10)
, (10) (11)
(11) , при которых существуют нетривиальные решения задачи (10) – (11), и отыскать эти решения.
, при которых существуют нетривиальные решения задачи (10) – (11), и отыскать эти решения.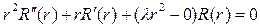
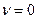 . Его общее решение
. Его общее решение
 следует, что с2=0. Таким образом,
следует, что с2=0. Таким образом,
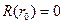 дает
дает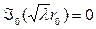 ,
,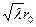 должно быть одним из нулей функции Бесселя
должно быть одним из нулей функции Бесселя 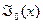 , т.е.
, т.е. ,
, - нуль функции
- нуль функции 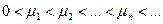 ,
,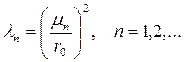 ,
, .
.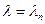 обще решение уравнения (9) имеет вид
обще решение уравнения (9) имеет вид .
.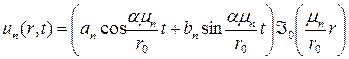
 , (12)
, (12) .
. , (1)
, (1) , (2)
, (2)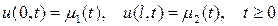 . (3)
. (3)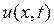 ,
, 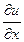 и
и  , рассматриваемые как функции t, являются функциями-оригиналами. Пусть U(x,p) есть изображение функции
, рассматриваемые как функции t, являются функциями-оригиналами. Пусть U(x,p) есть изображение функции  .
. ,
,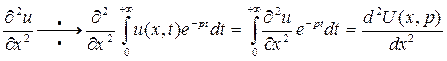 .
. .
. .
.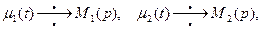 тогда граничные условия дают
тогда граничные условия дают .
. (4)
(4)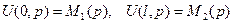 . (5)
. (5)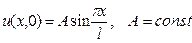 . Начальные скорости отсутствуют. Найти отклонение u(x,t) струны при t>0.
. Начальные скорости отсутствуют. Найти отклонение u(x,t) струны при t>0.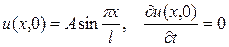
 .
.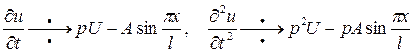 .
.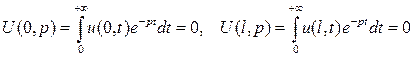
 , (*)
, (*)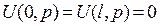 , (**)
, (**) .
.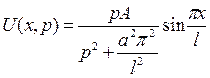 .
.