
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Вынужденные колебания струны с подвижными концами.
Рассмотрим колебания струны длины l, под действием внешней силы f(x,t), рассчитанной на единицу длины, причем концы струны не закреплены, а двигаются по заданному закону. Эта задача приводит к решению уравнения
при граничных условиях
и начальных условиях
К решению этой задачи метод Фурье непосредственно не применим. Однако, эта задача сводиться к задаче с нулевыми граничными условиями. Для этого введем вспомогательную функцию
Легко видеть, что
Таким образом, функция w(x,t) на концах отрезка
рис. 1 Решение задачи (1) – (3) ищем в виде
где v(x,t) – новая неизвестная функция. В силу выбора функции w(x,t) функция v=u-w удовлетворяет нулевым граничным условиям
и начальным условиям
Подставив u=v+w в уравнение (1), получим
или, учитывая выражение для w(x,t),
где
Таким образом, при
с граничными условиями
и начальными условиями
Пример:
Решение: Вводим вспомогательную функцию
Решение исходной задачи будем искать в виде
где v(x,t) – новая неизвестная функция. Для нее получаем уравнение
граничные условия
начальные условия
Задача (I) – (II) имеет очевидное решение v(x,t)=0, и это единственное решение. Тогда по формуле (*) получаем решение исходной задачи
Общая схема метода Фурье. Рассмотрим уравнение
где
и займемся изучением смешанной задачи для уравнения (1) при однородных граничных условиях
где Возможны граничные условия следующих типов: 1. 2. 3.
Ограничившись для простоты случаем струны с закрепленными концами, приходим к следующей задаче: найти решение u(x,t) уравнения
удовлетворяющее граничным условиям
и начальными условиями
Будем решать эту задачу методом Фурье.
1. Ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде
Подставляя u(x,t) в форме (4) в уравнение (1), получим
или
Получим
Чтобы получить нетривиальные решения уравнения (1) вида (4), удовлетворяющие граничным условиям (2), необходимо, чтобы функция Х(х) была нетривиальным решением уравнения (7), удовлетворяющим граничным условиям
В силу однородности уравнения (7) и граничных условий (8) собственные функции определяются с точностью до постоянного множителя. Выберем этот множитель так, чтобы
Собственные функции, удовлетворяющие (9), будем называть нормированными. 2. Обратимся к дифференциальному уравнению (6). Его общее решение при
где Каждая функция
будет решением уравнения (1), удовлетворяющим граничным условиям (2). 3. Составим формальный ряд
Если этот ряд, вместе с рядами, полученными из него двукратным почленным дифференцированием по x и t, сходиться равномерно, то сумма u(x,t) будет решением уравнения (1), удовлетворяющим граничным условиям (2). Для выполнения начальных условий (3) необходимо, чтобы
Таким образом, мы пришли к задаче о разложении произвольной функции в ряд Фурье по собственным функциям Xk(x) граничной задачи (7) – (8). Предполагая, что ряды (11) и (12) сходятся равномерно, можно найти коэффициенты ak и bk, умножив обе части равенства (11) и (12) на
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.0.53 (0.009 с.) |
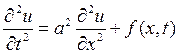 (1)
(1) (2)
(2)
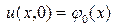 . (3)
. (3) (4)
(4) (5)
(5)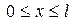 удовлетворяет условиям (2), а внутри этого отрезка она линейна по х (рис. 1). Говорят, что функция w(x,t) продолжает граничные условия в интервале 0<x<l.
удовлетворяет условиям (2), а внутри этого отрезка она линейна по х (рис. 1). Говорят, что функция w(x,t) продолжает граничные условия в интервале 0<x<l.

 (7)
(7) . (8)
. (8)
 ,
, .
.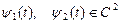 приходим к смешанной задаче с нулевыми граничными условиями для функции v(x,t): найти решение уравнения
приходим к смешанной задаче с нулевыми граничными условиями для функции v(x,t): найти решение уравнения
 .
.


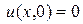

 (*)
(*) (I)
(I) (II)
(II)

 (1)
(1) для
для 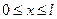 , так что уравнение (1) является уравнением гиперболического типа в области Q. Предположим, что
, так что уравнение (1) является уравнением гиперболического типа в области Q. Предположим, что ,
,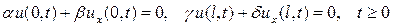
 - некоторые постоянные, причем
- некоторые постоянные, причем  .
.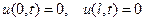 (струна с закрепленными концами (рис. 1 а));
(струна с закрепленными концами (рис. 1 а)); (струна со свободными концами (рис. 1 б));
(струна со свободными концами (рис. 1 б));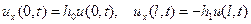 (упруго закрепленные концы (рис. 1 в)).
(упруго закрепленные концы (рис. 1 в)).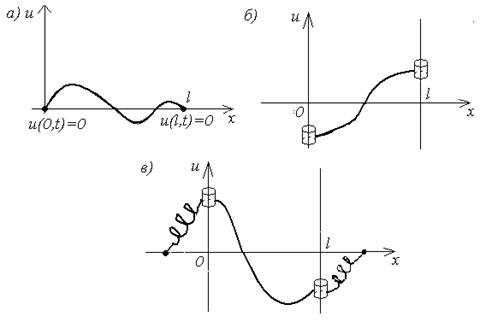
 (1)
(1) (2)
(2) (3)
(3) (4)
(4)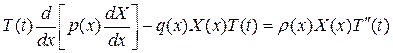 ,
, (5)
(5)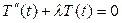 , (6)
, (6) (7)
(7)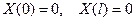 (8)
(8)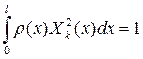 (9)
(9)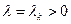 имеет вид
имеет вид ,
,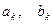 - произвольные постоянные.
- произвольные постоянные.
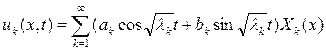 (10)
(10) , (11)
, (11)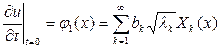 (12)
(12)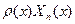 и проинтегрировав по х в пределах от 0 до l. Считая функции Xk(x) ортонормированными на отрезке [0,l], получим для коэффициентов Фурье функций
и проинтегрировав по х в пределах от 0 до l. Считая функции Xk(x) ортонормированными на отрезке [0,l], получим для коэффициентов Фурье функций  и
и 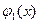 по системе {Xk(x)} следующие выражения:
по системе {Xk(x)} следующие выражения:



