
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Классификация дифференциальных уравнений с частными производными второго порядка.Стр 1 из 10Следующая ⇒
Лекция 7 Тема: Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Рассмотрим линейные ДУ 2-го порядка с постоянными коэффициентами с двумя независимыми переменными. Такие уравнения имеют вид
где Введем число
Согласно общей теории необходимо сделать замену переменных. Рассмотрим следующие случаи: 1. Гиперболический тип (∆>0). С помощью замены координат
Уравнение (10) приводится к виду:
2. Эллиптический тип (∆<0). С помощью замены координат
Уравнение (10) приводится к виду:
3. Параболический тип (∆=0). С помощью замены переменных
Уравнение (10) приводится к виду:
Замечание: Если
Для дальнейшего упрощения введем вместо
где
Подставляя выражения для производных в уравнение (15) и сокращая затем на
Параметр В результате получим
где γ – постоянная, выражающаяся через Производя аналогичные операции и для уравнений с постоянными коэффициентами:
Пример: Привести к каноническому виду уравнение
Решение: Так как Согласно формуле (12) делаем замену
Вычисляем частные производные:
Решая систему уравнений (*) относительно х, у находим формулы обратной замены.
Подставляя полученные выражения в уравнение, и приводя подобные получаем:
Умножение на -1 приводит уравнение к виду:
Далее делаем замену неизвестной функции:
Вычисляем частные производные функции u:
Подставляя эти выражения в уравнение и разделив на
Надо положить Тогда уравнение примет канонический вид:
Примеры:
Привести к каноническому виду 1. 2. 3. 4. 5. 6. 7. 8.
Лекция 8 Лекция 9 Лекция 10 Лекция 11.
Общая схема метода Фурье. Рассмотрим уравнение
где
и займемся изучением смешанной задачи для уравнения (1) при однородных граничных условиях
где Возможны граничные условия следующих типов: 1. 2. 3.
Ограничившись для простоты случаем струны с закрепленными концами, приходим к следующей задаче: найти решение u(x,t) уравнения
удовлетворяющее граничным условиям
и начальными условиями
Будем решать эту задачу методом Фурье. 1. Ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде
Подставляя u(x,t) в форме (4) в уравнение (1), получим
или
Получим
Чтобы получить нетривиальные решения уравнения (1) вида (4), удовлетворяющие граничным условиям (2), необходимо, чтобы функция Х(х) была нетривиальным решением уравнения (7), удовлетворяющим граничным условиям
В силу однородности уравнения (7) и граничных условий (8) собственные функции определяются с точностью до постоянного множителя. Выберем этот множитель так, чтобы
Собственные функции, удовлетворяющие (9), будем называть нормированными. 2. Обратимся к дифференциальному уравнению (6). Его общее решение при
где Каждая функция
будет решением уравнения (1), удовлетворяющим граничным условиям (2). 3. Составим формальный ряд
Если этот ряд, вместе с рядами, полученными из него двукратным почленным дифференцированием по x и t, сходиться равномерно, то сумма u(x,t) будет решением уравнения (1), удовлетворяющим граничным условиям (2). Для выполнения начальных условий (3) необходимо, чтобы
Таким образом, мы пришли к задаче о разложении произвольной функции в ряд Фурье по собственным функциям Xk(x) граничной задачи (7) – (8). Предполагая, что ряды (11) и (12) сходятся равномерно, можно найти коэффициенты ak и bk, умножив обе части равенства (11) и (12) на
Лекция 12.
Тема: Колебания круглой мембраны. Применение преобразований Лапласа к решению смешанной задачи.
Метод Фурье применяется также при изучении колебаний ограниченных тел, плоских или объемных. Рассмотрим задачу о свободных колебаниях под действием начальных возмущений однородной круглой мембраны радиуса r0 с центром в начале координат, закрепленной по краю. Уравнение колебаний мембраны имеет вид
Введем полярные координаты
запишем уравнение колебаний мембраны в виде:
граничными условиями
(мембрана закреплена по краю) и начальным условиям
Ограничимся важным частным случаем осесемметричных колебаний, когда начальные функции f и F не зависят от При этом предположении задача сводиться к отысканию решения u=(r,t) уравнения
при граничном условии
и начальных условиях
Применяя метод разделения переменных, будем искать нетривиальные решения уравнения (4), удовлетворяющие граничному условию (5), в виде
Подставляя функцию u(r,t) в форму (7) в уравнение (4) и разделяя переменные, получим
Равенства (8) приводят к двум обыкновенным ДУ
Итак, мы пришли к задаче на собственные значения: найти те значения параметра Запишем уравнение (10) в виде:
Это дифференциальное уравнение Бесселя с
Из условия
граничное условие
откуда следует, что число
где
откуда получаем собственные значения
и соответствующие собственные функции
При
Функция
будет решением уравнения (4), удовлетворяющему граничному условию (5). Решение u(x,r) исходной задачи (4) – (6) ищем в виде формального ряда
где
Если подставив an и bn в (12), ряд сходится равномерно, то мы поучаем решение задачи (4) – (6). Применение преобразований Лапласа к решению смешанной задачи.
Пусть требуется найти решение u(x,t) уравнения
удовлетворяющее начальным условиям
и граничными условиями
Применяя преобразование Лапласа по t, предположим, что
Так как операция дифференцирования по х и операция интегрирования по t в преобразовании Лапласа перестановочны, получим
(здесь величина р рассматривается как параметр, и вместо частных производных пишут обычные). По правилу дифференцирования оригиналов имеем
Отсюда, учитывая начальные условия (2), получаем
Пусть
Переходя к изображениям, сводим задачу (1) – (3) для уравнения с частными производными к граничной задаче для обыкновенного ДУ: найти решение U(x,p) уравнения
при граничных условиях
Пусть U(x,p) - решение задачи (4) – (5). Тогда функция u(x,t) (оригинал для U(x,p))будет решением исходной задачи (1) – (3). Пример: Струна l закреплена на концах x=0, x=l. Начальные отклонения струны определяются формулой Решение: Задача сводиться к решению уравнения
при начальных условиях
и граничных условиях Применим преобразование Лапласа. По правилу дифференцирования с учетом начальных условий получим
Граничные условия дают
Приходим к граничной задаче для ОДУ:
Решая уравнение (*) как линейное с постоянными коэффициентами, найдем
Из условий (**) получаем с1=с2=0, так что
Оригиналом для U(x,p) является функция
которая будет решением для (6) – (8).
Примеры: 1.
Лекция 13.
Задача Коши.
Рассмотрим однородное уравнение теплопроводности
отвечающее случаю
и начальному условию
Физический смысл задачи состоит в определении температуры однородного бесконечного стержня в любой момент времени t>0 по известной его температуре Предположим, что 1)
2) законны операции дифференцирования
Тогда, применяя преобразование Фурье к обеим частям уравнения (1) и условию (2), от задачи (1) - (2) перейдем к задаче Коши для ОДУ
(величина Решение задачи (5) – (6) имеет вид
Ранее мы установили, что
где Ф[ f ] – преобразование Фурье функции f(x). Отсюда, полагая
Таким образом, в правой части равенства (7) стоит произведение преобразований Фурье функций Пользуясь теоремой о свертке, равенство (7) можно представить в виде
Левая часть формулы (8) есть преобразование Фурье (по аргументу х) искомой функции u(x,t), так что ее можно представить так:
откуда, пользуясь выражением для свертки функций
Полученная формула дает решение исходной задачи (1) – (2) и называется интегралом Пуассона. . Пример: Найти решение задачи Коши
Решение: Пользуясь формулой Пуассона (9), получаем
Сделаем замену переменного
Тогда
Из (*) получаем
Таким образом, решение u(x,t) поставленной задачи определиться формулой
Лекция 14. Лекция 15.
Лекция 16.
Лекция 17. Тема: Уравнение Лапласа. Простейшим уравнением эллиптического типа является уравнение Лапласа
В случае функции u=u(x,t) двух независимых переменных х, у уравнение Лапласа имеет вид
и в случае функции одного аргумента имеем
Решениями уравнения (3) являются функции Определение: Функция Формулы Грина.
- первая формула Грина. Меняя в формуле (4) u и v местами, получим
Вычитая равенства (4) и (5) почленно, находим
Это – вторая формула Грина. Наконец, полагая в (4) u=v, получим
Это – третья формула Грина. Здесь всюду n – вектор внешней нормали к гладкой или кусочно-гладкой замкнутой поверхности Основная интегральная формула Грина. Для уравнения Лапласа на плоскости фундаментальное решение имеет вид
Здесь Г – граница области D, n – вектор внешней нормали к границе (рис. 1). Таким образом, всякая гармоническая в области D функция u(x,y) есть сумма двух потенциалов
логарифмического потенциала простого слоя и логарифмического потенциала двойного слоя соответственно.
Рис. 1. Лекция 18.
Интеграл Пуассона.
Преобразуем формулу (11) к более простому виду. Подставив в нее выражения для коэффициентов Фурье и меняя порядок суммирования и интегрирования, будем иметь
Положим для кратности
Подставляя это выражение в (14), получим
Полученная формула дает решение первой краевой задачи для уравнения Решение внешней задачи имеет вид
Можно показать, что если функция
удовлетворяет уравнению Примеры: 1. Найти функцию, гармоническую внутри круга радиуса 1) 2. Найти функцию, гармоническую внутри круга радиуса 1) 3. Найти функцию, гармоническую в кольце 1<r<2 такую, что 4. Найти решение уравнения Лапласа внутри круга 5. Найти решение уравнения Лапласа внутри круга 6. Найти решение уравнения Лапласа внутри круга 7. Найти решение уравнения Лапласа внутри круга
8. Найти решение уравнения Лапласа внутри круга 9. Найти решение уравнения Лапласа внутри круга 10. Найти решение уравнения Лапласа внутри круга 11. Найти решение уравнения Лапласа внутри круга
Тема: Классификация дифференциальных уравнений с частными производными второго порядка. Определение: Уравнением с частными производными второго порядка с двумя независимыми переменными
Аналогично записывается и для большего числа независимых переменных. Определение: Уравнение называется линейным относительно старших производных, если оно имеет вид
где Определение: Если Определение: Уравнение называется линейным, если оно линейно как относительно старших производных
где Определение: Если коэффициенты уравнения (3) независимы от Определение: Если Далее рассмотрим упрощения, т.е. приведения к каноническим (простейшим) формам. С помощью преобразования переменных
допускающего обратное преобразование, мы получаем новое уравнение, эквивалентное искомому, Естественно поставить вопрос «Как выбирать I. Рассмотрим линейное уравнение относительно старших производных (1).
Преобразуя производные к новым переменным, получаем
Подставляем (4) в уравнение (1), будем иметь
где
а функция Замечание: Если исходное уравнение линейно, т.е.
то
т.е. уравнение остается линейным. Выберем переменные
Пусть Если положить Лемма: 1. Если
2. Если Доказательство см. Тихонов А.Н., Самарский А.А. Определение: Уравнение (7) называется характеристическим для уравнения (1), а его интегралы – характеристиками. Полагая Если Уравнение (7) распадается на два уравнения:
Знак подкоренного выражения определяет тип уравнения (1).
Это уравнение мы будем называть в точке М уравнением · гиперболического типа, если · параболического типа, если · эллиптического типа, если Нетрудно убедиться в правильном соотношении В размеченных точках области определения уравнения может принадлежать различным типам. Пример: Уравнения
- гиперболические при всех х и у, уравнение
- параболическое при всех х и у,
- эллиптическое при всех х и у,
- эллиптическое при y>0, параболическое на линии у=0 и гиперболическое в полуплоскости y<0.
Приведение дифференциальных уравнений в частных производных к каноническому виду . Рассмотрим область G, во всех точках которой уравнение имеет один и тот же тип. Через каждую точку области G проходят две характеристики, причем для уравнений гиперболического типа характеристики действительны и различны, для уравнений эллиптического типа – различны, а для уравнений параболического типа обе характеристики действительны и совпадают между собой. Разберем каждый из этих случаев в отдельности. 1. Для уравнения гиперболического типа Полагая,
приводим уравнение (5) после деления на коэффициент при
где Это так называемая каноническая форма уравнения гиперболического типа. Часто используются второй канонической формой. Полагаем
где Тогда В результате уравнение (5) примет вид
2. Для уравнений параболического типа
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.234.234 (0.241 с.) |
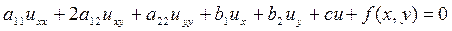 (10)
(10) - некоторые числа,
- некоторые числа, 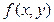 - некоторая функция.
- некоторая функция. . Приведем уравнение 2-го порядка к каноническому виду. Предположим, что хотя бы один из коэффициентов а11 или а22 отличен от нуля. Более того, меняя местами х и у, если это необходимо, можно считать, что
. Приведем уравнение 2-го порядка к каноническому виду. Предположим, что хотя бы один из коэффициентов а11 или а22 отличен от нуля. Более того, меняя местами х и у, если это необходимо, можно считать, что  . В данном случае характеристиками для уравнения (1) будут прямые:
. В данном случае характеристиками для уравнения (1) будут прямые: (11)
(11) (12)
(12) (13)
(13)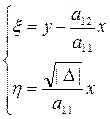 (14)
(14) (15)
(15) (16)
(16) (17)
(17) , то уравнение (10) приводится к виду (15) при помощи замены:
, то уравнение (10) приводится к виду (15) при помощи замены: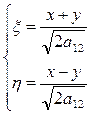 .
. новую функцию
новую функцию 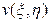 :
: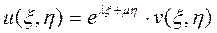 ,
, - неопределенные пока постоянные, тогда
- неопределенные пока постоянные, тогда
 , получаем
, получаем
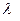 и
и  выбираем так, чтобы два коэффициента, например при первых производных обратились в ноль:
выбираем так, чтобы два коэффициента, например при первых производных обратились в ноль: 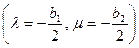 .
.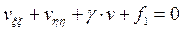 .
.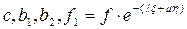 .
.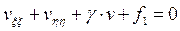 (эллиптический тип)
(эллиптический тип)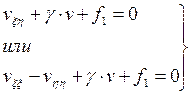 гиперболический тип)
гиперболический тип) (параболический тип)
(параболический тип)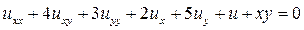
 , то это уравнение является уравнением гиперболического типа.
, то это уравнение является уравнением гиперболического типа. (*)
(*)

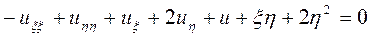

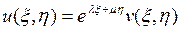
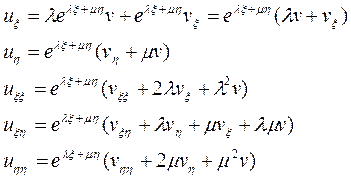
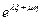 , получаем
, получаем
 , т.е.
, т.е.  .
.

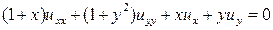
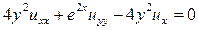
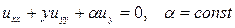

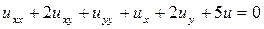


 (1)
(1) для
для 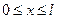 , так что уравнение (1) является уравнением гиперболического типа в области Q. Предположим, что
, так что уравнение (1) является уравнением гиперболического типа в области Q. Предположим, что ,
,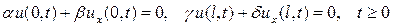
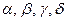 - некоторые постоянные, причем
- некоторые постоянные, причем  .
.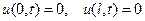 (струна с закрепленными концами (рис. 1 а));
(струна с закрепленными концами (рис. 1 а)); (струна со свободными концами (рис. 1 б));
(струна со свободными концами (рис. 1 б));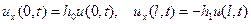 (упруго закрепленные концы (рис. 1 в)).
(упруго закрепленные концы (рис. 1 в)).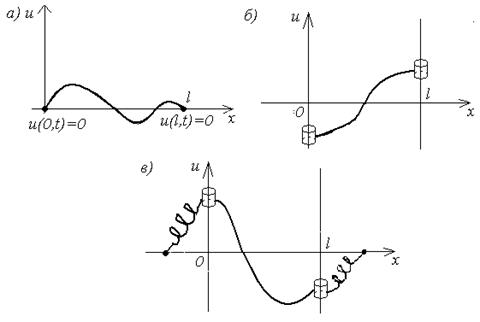
 (1)
(1) (2)
(2) (3)
(3) (4)
(4)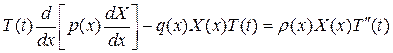 ,
, (5)
(5)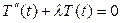 , (6)
, (6) (7)
(7)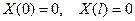 (8)
(8)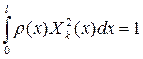 (9)
(9)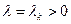 имеет вид
имеет вид ,
,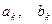 - произвольные постоянные.
- произвольные постоянные.
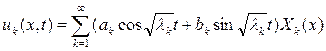 (10)
(10) , (11)
, (11)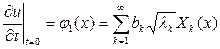 (12)
(12)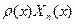 и проинтегрировав по х в пределах от 0 до l. Считая функции Xk(x) ортонормированными на отрезке [0,l], получим для коэффициентов Фурье функций
и проинтегрировав по х в пределах от 0 до l. Считая функции Xk(x) ортонормированными на отрезке [0,l], получим для коэффициентов Фурье функций  и
и 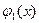 по системе {Xk(x)} следующие выражения:
по системе {Xk(x)} следующие выражения:
 .
. . Тогда отклонение точек мембраны будет функцией полярных координат
. Тогда отклонение точек мембраны будет функцией полярных координат 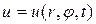 . Пользуясь выражением для оператора Лапласа
. Пользуясь выражением для оператора Лапласа 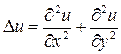 в полярных координатах,
в полярных координатах,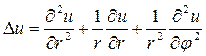 ,
, , (1)
, (1) (2)
(2) (3)
(3) . Ясно, что тогда любой момент времени t>0 величина отклонения мембраны не будет зависеть от полярного угла
. Ясно, что тогда любой момент времени t>0 величина отклонения мембраны не будет зависеть от полярного угла 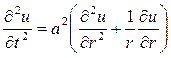 (4)
(4)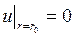 (5)
(5)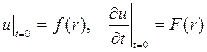 (6)
(6)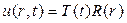 (7)
(7) (8)
(8) , (9)
, (9)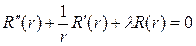 , (10)
, (10) (11)
(11) , при которых существуют нетривиальные решения задачи (10) – (11), и отыскать эти решения.
, при которых существуют нетривиальные решения задачи (10) – (11), и отыскать эти решения.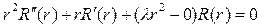
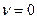 . Его общее решение
. Его общее решение
 следует, что с2=0. Таким образом,
следует, что с2=0. Таким образом,
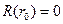 дает
дает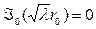 ,
,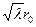 должно быть одним из нулей функции Бесселя
должно быть одним из нулей функции Бесселя  , т.е.
, т.е. ,
, - нуль функции
- нуль функции 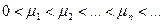 ,
,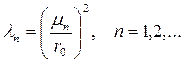 ,
, .
.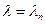 обще решение уравнения (9) имеет вид
обще решение уравнения (9) имеет вид .
.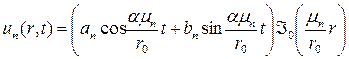
 , (12)
, (12) .
. , (1)
, (1) , (2)
, (2)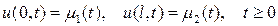 . (3)
. (3)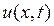 ,
, 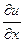 и
и  , рассматриваемые как функции t, являются функциями-оригиналами. Пусть U(x,p) есть изображение функции
, рассматриваемые как функции t, являются функциями-оригиналами. Пусть U(x,p) есть изображение функции  .
. ,
,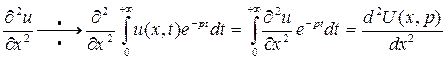 .
. .
. .
.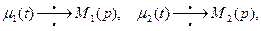 тогда граничные условия дают
тогда граничные условия дают .
. (4)
(4)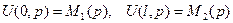 . (5)
. (5)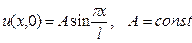 . Начальные скорости отсутствуют. Найти отклонение u(x,t) струны при t>0.
. Начальные скорости отсутствуют. Найти отклонение u(x,t) струны при t>0.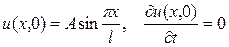
 .
.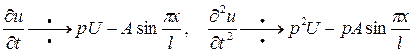 .
.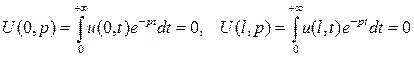
 , (*)
, (*)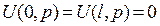 , (**)
, (**) .
.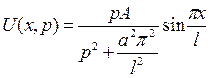 .
.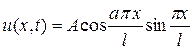
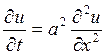
 , т.е. отсутствию источников. Задача Коши ставиться так: найти функцию
, т.е. отсутствию источников. Задача Коши ставиться так: найти функцию  , удовлетворяющую уравнению
, удовлетворяющую уравнению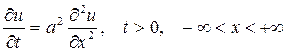 (1)
(1) (2)
(2) в момент времени t=0.
в момент времени t=0. настолько быстро, что существуют преобразования Фурье
настолько быстро, что существуют преобразования Фурье (3)
(3)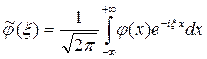 (4)
(4)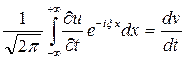
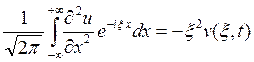 .
.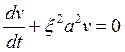 (5)
(5)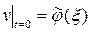 (6)
(6)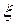 играет роль параметра).
играет роль параметра). (7)
(7) ,
,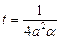 , получаем
, получаем .
.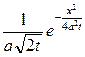 .
. (8)
(8) ,
,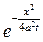 , имеем
, имеем (9)
(9)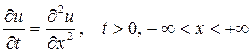

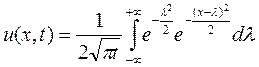
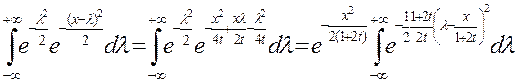 (*)
(*)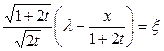 .
.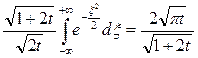 .
. .
.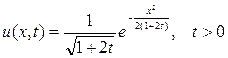 .
.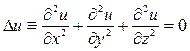 (1)
(1)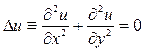 (2)
(2) . (3)
. (3) , где с1, с2 – произвольные постоянные.
, где с1, с2 – произвольные постоянные. называется гармонической в области
называется гармонической в области  , если
, если 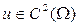 и удовлетворяет в области
и удовлетворяет в области  уравнению Лапласа (1).
уравнению Лапласа (1). (4)
(4)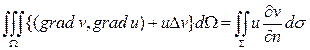 (5)
(5)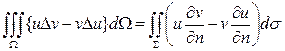 (6)
(6) (7)
(7)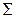 .
. . Можно получить интегральную формулу для гармонической функции двух аргументов:
. Можно получить интегральную формулу для гармонической функции двух аргументов: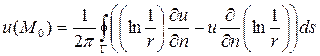

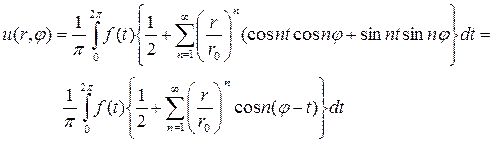 (14)
(14)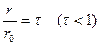 и проведем следующие тождественные преобразования:
и проведем следующие тождественные преобразования: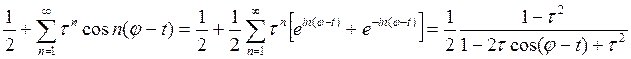 .
.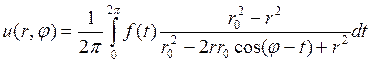 (15)
(15) внутри круга
внутри круга 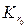 и называется интегралом Пуассона, а выражение
и называется интегралом Пуассона, а выражение 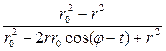 называют ядром Пуассона.
называют ядром Пуассона.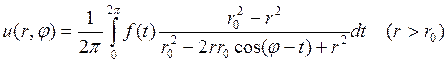 .
.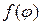 только непрерывна на границе круга
только непрерывна на границе круга 
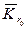 .
. с центром в начале координат и такую, что
с центром в начале координат и такую, что ; 2)
; 2) 
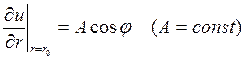 ; 2)
; 2) 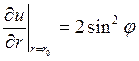
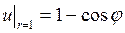 ,
, 
 , принимающее на границе круга
, принимающее на границе круга 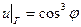 .
. , принимающее на границе круга
, принимающее на границе круга 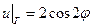 .
. , принимающее на границе круга
, принимающее на границе круга 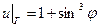 .
.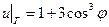 .
.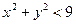 , принимающее на границе круга
, принимающее на границе круга  .
.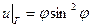 .
. .
.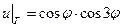 .
. называется соотношением между независимой функцией
называется соотношением между независимой функцией  и ее частными производными второго порядка включительно:
и ее частными производными второго порядка включительно: (1)
(1) (2)
(2)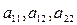 являются функциями
являются функциями  и
и  .
.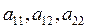 зависят не только от х и
зависят не только от х и  , а являются функциями
, а являются функциями  , то такое уравнение называется квазилинейным.
, то такое уравнение называется квазилинейным.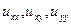 , так и относительно функции
, так и относительно функции 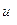 и ее первых производных
и ее первых производных  :
: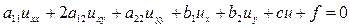 (3)
(3) - функции только от
- функции только от 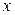 и
и 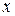 и
и  , то уравнение называется однородным.
, то уравнение называется однородным.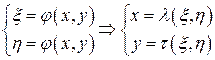 ,
,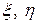 , чтобы уравнение в этих переменных имело наиболее простую форму?»
, чтобы уравнение в этих переменных имело наиболее простую форму?»
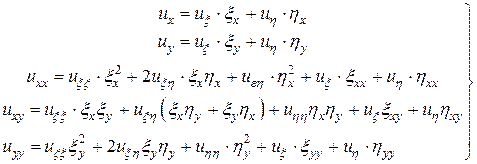 (4)
(4)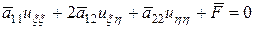 (5)
(5)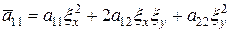
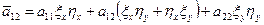
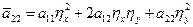 ,
, не зависит от вторых производных.
не зависит от вторых производных.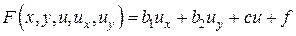 ,
,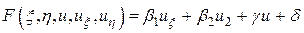 ,
, и
и 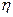 так, чтобы коэффициент
так, чтобы коэффициент  был равен нулю. Рассмотрим уравнение с частными производными первого порядка.
был равен нулю. Рассмотрим уравнение с частными производными первого порядка. (6)
(6)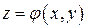 какое-нибудь частное решение этого уравнения.
какое-нибудь частное решение этого уравнения.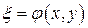 , то коэффициент
, то коэффициент 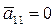 . Таким образом, упомянутая выше задача о выборе новых независимых переменных связана с решением уравнения (6).
. Таким образом, упомянутая выше задача о выборе новых независимых переменных связана с решением уравнения (6). , то соотношение
, то соотношение  представляет собой общий интеграл обыкновенного дифференцированного уравнения
представляет собой общий интеграл обыкновенного дифференцированного уравнения (7)
(7)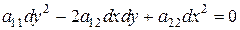 , то функция
, то функция  есть общий интеграл уравнения (7), мы обращаем в нуль коэффициент при
есть общий интеграл уравнения (7), мы обращаем в нуль коэффициент при  .
. , то полагая
, то полагая  , мы обратим в нуль и коэффициент при
, мы обратим в нуль и коэффициент при  , т.е.
, т.е. 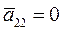 .
.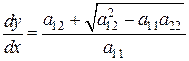 (8)
(8) (9)
(9)
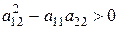 ,
, ,
,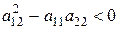 .
.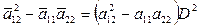 , где
, где 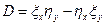 , из которого следует инвариантность уравнения при преобразовании переменных.
, из которого следует инвариантность уравнения при преобразовании переменных. и
и 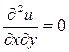
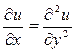

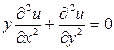
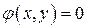 определяют действительные семейства характеристик.
определяют действительные семейства характеристик.
 к виду
к виду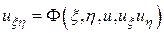 ,
, .
. , т.е.
, т.е.  ,
, и
и  - новые переменные.
- новые переменные. ,
, 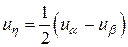 ,
,  .
.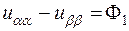 ,
,  .
.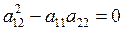 . Уравнения (8) и (9) совпадают, и мы получаем один общий интеграл уравнения (7):
. Уравнения (8) и (9) совпадают, и мы получаем один общий интеграл уравнения (7):


