
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Решение задачи Дирихле для круга методом Фурье. Интеграл Пуассона. ⇐ ПредыдущаяСтр 10 из 10
Задача ставиться так: найти функцию
непрерывную в замкнутой области
где В силу однозначности искомого решения оно должно быть периодическим по Уравнение (1) в полярных координатах имеет вид
Будем искать частные решения уравнения (3) в виде
Подставляя
откуда
Из условия
В частности, Полагая в уравнении (6) (уравнении Эйлера)
Отсюда
При n=0 из (6) находим
Решение внутренней задачи Дирихле будем искать в виде ряда
где коэффициенты При r=r0 имеем
Запишем разложение
где
Сравнивая ряды (8) и (9), получаем
Таким образом, формальное решение внутренней задачи Дирихле для круга представимо в виде ряда
где коэффициенты Решение внешней задачи Дирихле следует искать в виде ряда
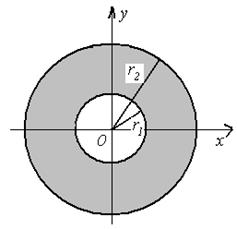
где коэффициенты Для кольцевой области
коэффициенты которого
Рис. 1. Пример: найти функцию, гармоническую внутри круга радиуса Решение: Задача сводится к решению задачи Дирихле для уравнения
Из граничного условия имеем
Отсюда в силу ортогональности системы функций
Искомое решение
Интеграл Пуассона.
Преобразуем формулу (11) к более простому виду. Подставив в нее выражения для коэффициентов Фурье и меняя порядок суммирования и интегрирования, будем иметь
Положим для кратности
Подставляя это выражение в (14), получим
Полученная формула дает решение первой краевой задачи для уравнения Решение внешней задачи имеет вид
Можно показать, что если функция
удовлетворяет уравнению Примеры: 1. Найти функцию, гармоническую внутри круга радиуса 1) 2. Найти функцию, гармоническую внутри круга радиуса 1) 3. Найти функцию, гармоническую в кольце 1<r<2 такую, что 4. Найти решение уравнения Лапласа внутри круга 5. Найти решение уравнения Лапласа внутри круга 6. Найти решение уравнения Лапласа внутри круга 7. Найти решение уравнения Лапласа внутри круга 8. Найти решение уравнения Лапласа внутри круга 9. Найти решение уравнения Лапласа внутри круга 10. Найти решение уравнения Лапласа внутри круга 11. Найти решение уравнения Лапласа внутри круга
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1873; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.135.224 (0.01 с.) |
 , удовлетворяющую внутри круга
, удовлетворяющую внутри круга 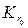 радиуса
радиуса  с центром в начале координат уравнению Лапласа
с центром в начале координат уравнению Лапласа , (1)
, (1)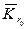 и принимающую заданные значения на границе круга,
и принимающую заданные значения на границе круга, (2)
(2)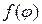 - достаточно гладкая функция, периодическая с периодом
- достаточно гладкая функция, периодическая с периодом  .
. с периодом
с периодом  ,
,  . Из непрерывности решения
. Из непрерывности решения  (3)
(3) . (4)
. (4)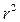 , получим
, получим ,
, (5)
(5) (6)
(6)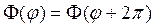 , а из (5) находим
, а из (5) находим  , так что
, так что .
. .
.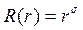 , при
, при  получаем
получаем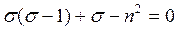 .
. и, следовательно,
и, следовательно, .
. .
. , (7)
, (7) определяются из граничного условия (2).
определяются из граничного условия (2).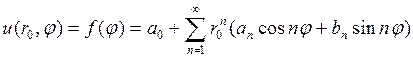 , (8)
, (8) , (9)
, (9)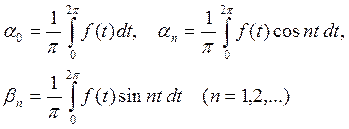 , (10)
, (10)
 (11)
(11) определяются по формулам (10).
определяются по формулам (10). , (12)
, (12) определяются из граничного условия
определяются из граничного условия  .
. , образованной двумя концентрическими окружностями с центром в точке 0 радиусов
, образованной двумя концентрическими окружностями с центром в точке 0 радиусов  и
и 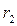 (рис. 1), решение задачи ищется в виде ряда
(рис. 1), решение задачи ищется в виде ряда (13)
(13) (n=1, 2, …) определяются из граничных условий
(n=1, 2, …) определяются из граничных условий
 с центром в начале координат и такую, что
с центром в начале координат и такую, что 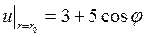 .
. при граничном условии
при граничном условии 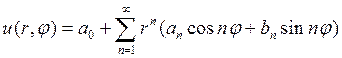 .
. .
.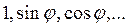 на отрезке
на отрезке  получаем
получаем
 , или
, или  .
.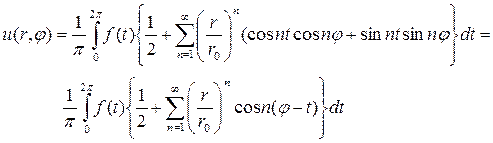 (14)
(14)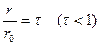 и проведем следующие тождественные преобразования:
и проведем следующие тождественные преобразования: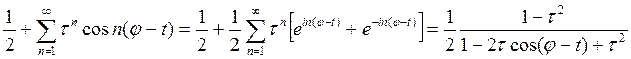 .
.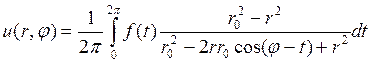 (15)
(15)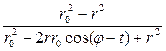 называют ядром Пуассона.
называют ядром Пуассона.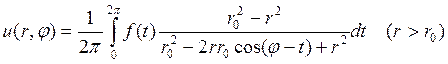 .
.
 ; 2)
; 2) 
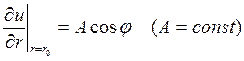 ; 2)
; 2) 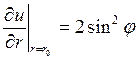
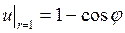 ,
, 
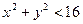 , принимающее на границе круга
, принимающее на границе круга 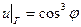 .
. , принимающее на границе круга
, принимающее на границе круга 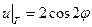 .
. , принимающее на границе круга
, принимающее на границе круга 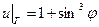 .
.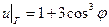 .
.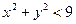 , принимающее на границе круга
, принимающее на границе круга  .
.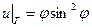 .
. .
.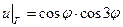 .
.


