Дипольные свойства волны деполяризации и реполяризации на поверхности одиночного мышечного волокна. Понятие о векторе

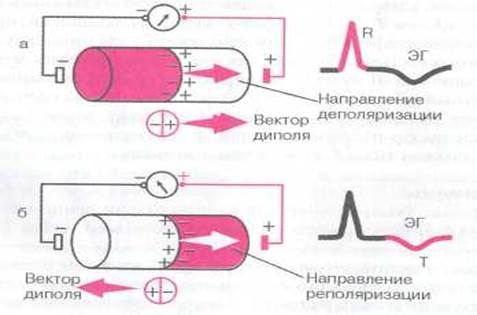
В клинической электрокардиографии электрические явления, воз­никающие на поверхности возбудимой среды (волокна, сердца), при­нято описывать с помощью так называемой дипольной концепции рас­пространения возбуждения в миокарде. Это значительно упрощает трактовку всех электрокардиографических изменений, доэтому необ­ходимо более подробно рассмотреть некоторые свойства сердечного диполя.

Как видно на рисунке 1.8, процесс распространения волны де­поляризации и волны реполяризации по одиночному мышечному волокну можно условно представить как перемещение двойного слоя зарядов, расположенных на границе возбужденного (—) и не­возбужденного (+) участков волокна. Эти заряды, равные по вели­чине и противоположные по знаку, находятся на бесконечно малом расстоянии друг от друга и обозначаются как элементарные сер­дечные диполи. Положительный полюс диполя (+) всегда обращен в сторону невозбужденного, а отрицательный полюс (—) — в сторо­ну возбужденного участка миокардиального волокна. Диполь со­здает элементарную ЭДС.

 

 

 

Рис. 1.8. Направление вектора сердечного диполя при деполяризации (а) и реполяризации (б) одиночного мышечного волокна

ЭДС диполя — векторная величина, которая характеризуется не только количественным значением потенциала, но и направлением - пространственной ориентацией от (—) к (+).

Запомните! Условно принято считать, что вектор любого диполя направлен от его отрицательного полюса к положительному, как это показа­но на рисунке 1.8.

На рисунке также хорошо видно, что направление движения вол­ны деполяризации по одиночному мышечному волокну всегда сов­падает с направлением вектора диполя, а направление движения волны реполяризации противоположно ориентации вектора диполя.

Теперь, чтобы описать, как будет выглядеть форма ЭГ при любых направлениях движения волны де- и реполяризации, вам необходимо хорошо запомнить всего три общих правила.

 

 

Запомните! Правило первое. Если в процессе распространения возбуждения вектор диполя направлен в сторону положительного электрода от­ведения, то на ЭГ мы получим отклонение вверх от изолинии — положительный зубец ЭГ (рис. 1.9, а). Правило второе. Если вектор диполя направлен в сторону отри­цательного электрода отведения, то на ЭГ мы зафиксируем отри­цательное отклонение, вниз от изолинии, т.е. отрицательный зу­бец ЭГ (рис. 1.9,6). Правило третье. Наконец, если вектор диполя расположен перпендикулярно к оси отведения, то на ЭГ записывается изоли­ния, т.е. отсутствуют положительные или отрицательные отклоне­ния ЭГ(рис. 1.9, в).

Эти простые правила позволят вам самостоятельно определить конфигурацию ЭГ при любом расположении активного положитель­ного электрода и любом направлении движения волны де- и реполя­ризации, изображенных на рисунке 1.10. При решении этих заданий обязательно воспользуйтесь следующим алгоритмом:

1) определите и отметьте на схеме полярность диполя во время де-и реполяризации;

2) обозначьте стрелкой направление вектора диполя во время де- и реполяризации;

3) схематично зарисуйте конфигурацию ЭГ во время де- и реполя­ризации.

 

Рис. 1.9. Три варианта формы ЭГ одиночного мышечного волокна в зависи­мости от направления вектора сердечного диполя по отношению к положи­тельному (активному) электроду отведения

 

Рис. 1.10. Задание 1. Определите форму ЭКГ во время де- и реполяризации по отношению к положительному (активному) электроду отведения: (Де - деполяризация; Ре — реполяризация).

Рис. 1.11. Форма ЭГ при различном направлении де- и реполяризации (этало­ны правильных ответов к заданию на рисунке 1.10). Красным цветом обозначены участки мышечного волокна, находящиеся в состоянии возбуждения.

 

А теперь проверьте правильность вашего решения, взглянув на рисунке 1.11.