
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод стандартных коэффициентовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод стандартных коэффициентов не является универсальным. Однако он нашел широкое применение благодаря своей простоте. В основу метода положена связь между переходной характеристикой h (t) и основной ПФ системы управления F(s). Вид переходной характеристики определяется значением нулей zm и полюсов pn основной ПФ системы. Для ряда типовых ПФ найдены " оптимальные " распределения нулей и полюсов, обусловливающие наиболее благоприятные переходные характеристики h (t) с точки зрения динамики синтезируемой САР. Каждому такому оптимальному распределению нулей и полюсов соответствуют вполне определенные значения коэффициентов полиномов числителя и знаменателя основной ПФ системы, которые называют стандартными. Синтез САУ этим методом начинают с приведения основной ПФ системы (2.31)
к нормированному виду (форме Вышнеградского). Для этого аргумент ПФ s заменяют аргументом
где
Если САУ описывается уравнением второго порядка (n = 2), величина Приведение ПФ системы F(s) к нормированному виду F(s *)изменяет длительность процесса регулирования с t рна tр. Безразмерное время регулирования tр, соответствующее нормированной ПФ, и реальное время t р, соответствующее исходной ПФ F(s), связаны следующим образом:
При этом величину Реальные САУ характеризуются небольшим порядком высшей производной числителя m. Поэтому стандартные коэффициенты определены для трех типовых нормированных ПФ:
1) не содержащих нулей (m = 0):
2) с одним нулем (m = 1):
3) с двумя нулями (m = 2):
Названные коэффициенты A 1– An -1обусловливают наименьшую длительность процесса регулирования t р. Обычно стандартные коэффициенты сводят в таблицы, в которых также указывают безразмерное время tрсоответственно порядку ПФ n. Если САУ описывается первой типовой ПФ вида (3.16), т.е. не содержит нулей, наименьшей длительности переходного процесса (t р = t мин) достигают биномиальными коэффициентами A 1, A 2, …, An -1. В этом случае коэффициенты характеристического уравнения являются коэффициентами бинома Ньютона (s + 1) n. При биномиальных коэффициентах корни характеристического уравнения являются кратными (вещественными). Коэффициенты уравнений от первого (n = 1) до пятого (n = 5) порядка сведены в таблицу 3.1, которая содержит также соответственно безразмерное время регулирования tр. Переходные характеристики САУ с ПФ вида (3.16) и n = 1 ¸ 5 изображены на рисунке 3.17 и свидетельствуют об отсутствии перерегулирования, т.е. являются монотонными. Процесс регулирования в САУ второго порядка (n = 2) названного качества достигается при коэффициенте демпфирования x = 1 (см. переходную характеристику 1 на рисунке 3.18).
Установлено оптимальное отношение m = g/h, которое обусловливает наименьшее безразмерное время регулирования tрсреди трех названных случаев. Соответствующие стандартные коэффициенты указаны в таблице 3.2.
На рисунке 3.18 показаны эталонные переходные характеристики САУ с ПФ вида (3.16)
и стандартными коэффициентами соответственно 1) 1; A 1= 2,00; 1 (x = 1); 2) 1; A 1= 1,50; 1 (x = 0,75); 3) 1; A 1= 1,38; 1 (x = 0,69). При синтезе АР стандартные коэффициенты используют следующим образом. Если синтезируемая САР (рисунок 3.19) содержит, например, П‑регулятор, то выбору подлежит коэффициент усиления регулятора K АР.
В первую очередь определяют ПФ разомкнутой системы по (2.27)
и основную ПФ системы по (2.32)
Полученную основную ПФ системы нормируют следующим образом:
Поскольку ПФ не содержит нулей (m = 0), эталонной функцией является типовая ПФ вида (3.19) при n = 2
Для определения неизвестного коэффициента K АРсравнивают коэффициенты характеристических полиномов двух основных ПФ F(s) и Fэ(s) и получают систему алгебраических уравнений
На этом этапе синтеза АР система уравнений кроме K АРсодержит еще два неизвестных A 1и W0. Коэффициент A 1должен иметь стандартное значение. Его выбирают по таблицам стандартных коэффициентов в зависимости от принятой эталонной переходной характеристики (рисунок 3.18). Эталонную характеристику h э(t) выбирают, в свою очередь, в соответствии с технологическим регламентом. Второе неизвестное рассчитывают, используя первое уравнение системы, по формуле
Затем определяют искомый коэффициент усиления П-регулятора
Если технологическим регламентом ограничена длительность процесса регулирования t р £ tmax, необходимо рассчитать действительное время регулирования t ри убедиться в выполнении требования регламента. Для этого сначала определяют безразмерное время регулирования tрпо таблицам или по эталонной переходной характеристике h э(t) (рисунок 3.18). Затем вычисляют действительное время регулирования t рпо формуле
В частности, если в рассматриваемом примере параметризации П‑регулятора (рисунок 3.19) в качестве эталонного принять монотонный процесс регулирования (переходная характеристика 1 на рисунке 3.18) и биномиальные коэффициенты, то в соответствии с таблицей 3.1 эталонная ПФ системы принимает вид
Если ОР характеризуется следующими параметрами K ОР = 0,1 и T ОР = 5, то частота собственных колебаний САР
Окончательно искомый коэффициент усиления П-регулятора
Действительное время регулирования при tр= 4,8 (см. таблицу 3.1)
Рассмотренные комбинации стандартных коэффициентов, связанные с кратным или близким к нему распределением корней характеристического уравнения САУ, эффективны при параметрической оптимизации систем, ПФ которых не имеют нулей. В противном случае процесс регулирования сопровождается заметным перерегулированием (s > 5 %). Для недопущения этого предложены другие комбинации стандартных коэффициентов, которым соответствует иное расположение корней характеристического уравнения САУ. В случае САУ с основной ПФ типа (3.17) с одним нулем (m = 1) корни характеристического уравнения рекомендуется располагать на отрицательной вещественной полуоси в арифметической прогрессии. Коэффициенты характеристического полинома типовой ПФ вида (3.17) указаны в таблице 3.3.
Примером названной САУ становится рассмотренная в предыдущем примере система при изменении простейшего пропорционального закона регулирования на изодромное (рисунок 3.20).
При использовании ПИ‑регулятора ПФ системы имеет вид
Основная ПФ в нормированном виде
содержит только один ноль (m = 1). Поэтому эталонной является типовая ПФ вида (3.17) при (n = 3)
Сравнивая коэффициенты характеристических полиномов основных ПФ F(s) и Fэ(s), получают систему алгебраических уравнений
Согласно таблице 3.3 стандартные коэффициенты равны A 1 = 6,35 и A 2 = 5,10. Поскольку ОР сохраняет свои параметры без изменения, из первого уравнения этой системы следует, что
С помощью двух других алгебраических уравнений определяют искомые параметры настройки ПИ-регулятора
Действительное время регулирования
Переходная характеристика САР с ПИ-регулятором показана на рисунке 3.21. В случае САУ с основной ПФ типа (3.18) с двумя нулями (m = 2) корни характеристического уравнения рекомендуется располагать на отрицательной вещественной полуоси в геометрической прогрессии. Коэффициенты характеристического полинома ПФ вида (3.18) представлены в таблице 3.4.
Минимизацией квадратичного функционала J 20получены стандартные коэффициенты типовой ПФ вида (3.16), которые представлены в таблице 3.5.
Д.Грехем и Р.Летроп получили стандартные коэффициенты типовой ПФ вида (3.16) (таблица 3.6) при минимизации интеграла от абсолютного значения ошибки J 10.
В таблице 3.7 представлены стандартные коэффициенты Баттерворта (идеальный фильтр), которые раньше других начали применять при оптимизации электроприводов.
Внешнее отличие названных коэффициентов проявляется их симметричным распределением подобно биномиальным коэффициентам. Однако переходная характеристика САУ приобретает перерегулирование и колебательностью превосходит аналогичные характеристики. Время регулирования, обусловленное коэффициентами Баттерворта, также самое большое среди рассмотренных ранее. Тем не менее в этом случае САУ обладает наиболее широкой полосой пропускания гармонических полезных сигналов при заданной статической ошибке регулирования. Другими словами, модуль АЧХ системы управления
Метод корневого годографа
Метод корневого годографа (МКГ) применяется при анализе и синтезе линейных САУ. С помощью корневого годографа системы можно оценить ее устойчивость и качество регулирования. Однако МКГ наиболее эффективен при синтезе корректирующих устройств САУ. Корневым годографом называют совокупность траекторий, которые описывают корни характеристического уравнения замкнутой САУ на комплексной плоскости при изменении одного из параметров системы от 0 до ¥. Варьируемым может быть любой из параметров, линейно входящий в характеристическое уравнение. Типичной является задача исследования влияния коэффициента усиления автоматического регулятора и параметров корректирующего устройства на очертания годографа. Суть МКГ наиболее просто оценить на примере следящей системы, структурная схема которой изображена на рисунке 2.9. В простейшем случае ПФ разомкнутой САУ может быть подобна ПФ А-звена первого порядка
Единственный вещественный полюс ПФ
В случае САУ второго порядка ПФ разомкнутой системы
имеет два вещественных полюса
ПФ разомкнутой САУ может быть подобна ПФ колебательного звена
и соответственно иметь пару комплексно-сопряженных полюсов p 1, 2 = a ± j b при x < 1. Действительную часть полюса a называют коэффициентом затухания (сравни с декрементом затухания), так как a характеризует быстроту затухания колебаний разомкнутой САУ. Мнимую часть полюса b называют частотой собственных колебаний разомкнутой САУ. Коэффициент демпфирования x и постоянная времени T разомкнутой системы определяют названные величины следующим образом:
Корневой годограф замкнутой системы показан на рисунке 3.24. В качестве последнего примера на рисунке 3.25 изображен корневой годограф САУ, которая в разомкнутом состоянии имеет ПФ третьего порядка соответственно структурной схеме (рисунок 3.26):
Рассмотренные примеры достаточно иллюстрируют свойства КГ замкнутых САУ /51, 56/: 1) количество ветвей КГ равно порядку характеристического уравнения САУ D (s) = 0, т.е. количеству полюсов основной ПФ системы F(s); 2) ветви КГ начинаются при K = 0 в полюсах ПФ разомкнутой САУ p 1, p 2, …, pn;
3) при K ® ¥ m ветвей КГ стремятся к m нулям ПФ z 1, z 2, …, zm. Остальные n – m ветвей устремляются в бесконечность; 4) КГ являются непрерывными кривыми или отрезками прямых, обусловленными изменением коэффициента усиления K от 0 до ¥; 5) КГ, не лежащие на оси вещественных чисел, симметричны относительно этой оси; 6) прямолинейные участки годографов, лежащие на оси вещественных чисел, обусловлены только вещественными полюсами и нулями (рисунки 3.22, 3.23 и 3.25); 7) в точках пересечения ветвей КГ с осью вещественных чисел два вещественных корня сливаются и далее превращаются в комплексно-сопряженные (рисунки 3.23 и 3.25); 8) точки пересечения ветвей КГ с осью мнимых чисел обусловлены чисто мнимыми корнями (рисунки 3.25). Самой трудоемкой операцией МКГ является построение годографа. Наиболее известны методы У.Р.Эванса, Э.Г.Удермана, К.Ф.Теодорчика- Г.А.Бендрикова, позволяющие построить КГ системы даже вручную. Современные системы компьютерной математики (MATLAB, MathCAD, Maple) и моделирования САУ (МВТУ, SystemView) содержат встроенные функции автоматического построения и анализа КГ систем управления /12, 58/. Наиболее эффективно применение ПК при синтезе корректирующих устройств САУ методом доминирующих полюсов. Этот метод наряду с методом компенсации можно рассматривать как разновидность МКГ. Понятие доминирующих (преобладающих) полюсов составляет основу метода доминирующих полюсов. Считают, что динамические свойства САУ определяет пара комплексно-сопряженных полюсов основной ПФ системы s 1, 2= -a ± j b,
называемых доминирующими. Другими словами, в качестве ММ синтезируемой САУ принимают К-звено с ПФ вида (2.19), т.е. принимают равенство
и подобие свойств замкнутой САУ и К-звена. На первом этапе синтеза решают задачу определения доминирующих полюсов по заданным показателям качества синтезируемой САУ. Если заданы время регулирования t р, перерегулирование s или показатель колебательности M, действительную и мнимую части полюсов рассчитывают по следующим формулам:
Затем наносят на комплексную плоскость вычисленные таким образом доминирующие полюсы s 1, 2. Там же указывают полюсы pn и нули zm неизменяемой части САУ, которые определяют по ПФ этой части W н(s). Под ПФ неизменяемой части системы W н(s) понимают ПФ разомкнутой нескорректированной САУ. Второй этап синтеза заключается в отыскании дополнительных полюсов и нулей, принадлежащих корректирующему устройству (КУ). Их размещают на комплексной плоскости так, чтобы КГ скорректированной САУ проходил около доминирующих полюсов s 1, 2. Рекомендуется скомпенсировать нулями ближайшие к мнимой оси полюсы неизменной части САУ для того, чтобы влияние доминирующих полюсов s 1и s 2на динамику системы было действительно определяющим. Наконец, в случае необходимости увеличения коэффициента передачи системы K до заданного значения, вводят диполь. Диполем называют близко расположенные друг к другу дополнительные полюс и ноль. Введение диполя позволяет увеличить коэффициент передачи без заметного изменение показателей качества САУ. По окончании коррекции составляют ПФ корректирующего устройства W ку(s), основываясь на введенных полюсах и нулях.
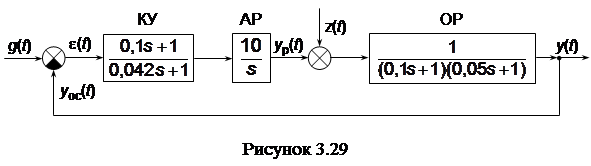
Примером /51/ САР, требующей коррекции своих динамических свойств, служит система, структурная схема которой изображена на рисунке 3.26. Переходная характеристика САР h н(t) показана на рисунке 3.27. Очевидно, что требования к процессу регулирования
не выполнены. Необходимо синтезировать последовательное КУ, обеспечивающее выполнение указанных требований при K ³ 10. Приняв первоначально t р = 0,5 и s = 0,2, согласно (3.21) рассчитывают доминирующие полюсы
Найденные доминирующие полюсы s 1, 2лежат вдали от КГ нескомпенсированной САР (НСК на рисунке 3.28). Неизменяемая часть САУ обладает полюсами p 1 = 0, p 2 = -10 и p 3 = -20. Ближайший из них к мнимой оси полюс p 2 = -10 необходимо скомпенсировать нулем КУ Таким образом, ПФ последовательного КУ
Структурная схема скомпенсированной САР показана на рисунке 3.29. Переходная характеристика системы h ск(t) изображена на рисунке 3.27.
Синтезированное КУ относят к инерционным устройствам ПД-типа, описываемым ПФ общего вида
В рассматриваемом примере
так как Различают опережающую (| p ку| > | z ку|) и запаздывающую (| p ку| < | z ку|) коррекции. Следовательно, синтезировано ПД-устройство опережающего или форсирующего типа. Положительное ПД-воздействие (см. знак "+" в числителе ПФ) форсирует, т.е. ускоряет, процесс регулирования. Форсирующее действие КУ обусловлено начальным "всплеском" переходной характеристики h (t) ПД-звена (см. таблицу 2.2). Поэтому включение КУ названного типа в САУ повышает быстродействие последних (см. рисунок 3.27). Наряду с последовательными КУ ПД-типа широко применяют корректирующие ПИ- и ПИД-звенья. ПИ-звенья включают в контур регулирования в тех случаях, когда основные показатели качества САУ – длительность процесса регулирования t ри перерегулирование s - удовлетворяют заданным требованиям, но коэффициент усиления мал. Его необходимо увеличить для уменьшения статической ошибки регулирования e g, см. равенство (2.42). При этом требуется сохранить неизменными показатели качества САУ t ри s. ПИД-звенья применяют в тех случаях, когда необходимо одновременно увеличить коэффициент усиления, повысить быстродействие САУ и уменьшить динамическое отклонение выходной величины ymax. Выбор параметров названных КУ осуществляют МКГ аналогично синтезу ПД-звена в рассмотренном примере.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.29.0 (0.016 с.) |

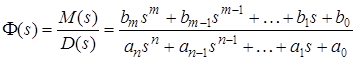
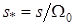 и делят ее числитель и знаменатель на
и делят ее числитель и знаменатель на  . В результате получают нормированную ПФ (индекс аргумента "*" опущен):
. В результате получают нормированную ПФ (индекс аргумента "*" опущен):
 ;
;  ; …;
; …; 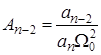 ;
;  ;
; ;
;  ; …;
; …;  ;
; – среднегеометрическое значение корней характеристического уравнения замкнутой САУ D (s) = 0.
– среднегеометрическое значение корней характеристического уравнения замкнутой САУ D (s) = 0. есть частота собственных колебаний системы.
есть частота собственных колебаний системы. .
. (3.16)
(3.16) (3.17)
(3.17) (3.18)
(3.18)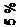
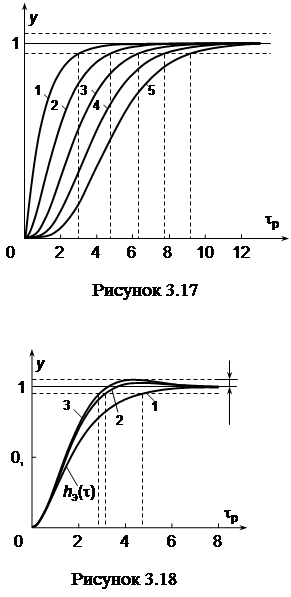 Если в процессе регулирования допускается незначительное перерегулирование, т.е. переходная характеристика может быть апериодической, рекомендуется принять коэффициент демпфирования x = 0,7 ¸ 0,8. Известно, что при таком демпфировании переходные процессы в системе второго и более высоких порядков затухают быстрее, чем в случае x = 1. В результате длительность процесса регулирования будет меньше (см. переходную характеристику 2 на рисунке 3.18). Кратность корней характеристического уравнения утрачивается, поскольку они становятся комплексными. Все комплексные корни (и один вещественный при нечетном n) располагаются на одинаковом расстоянии h от оси мнимых чисел. Мнимые части корней образуют арифметическую прогрессию с разностью g и первым членом прогрессии также g.
Если в процессе регулирования допускается незначительное перерегулирование, т.е. переходная характеристика может быть апериодической, рекомендуется принять коэффициент демпфирования x = 0,7 ¸ 0,8. Известно, что при таком демпфировании переходные процессы в системе второго и более высоких порядков затухают быстрее, чем в случае x = 1. В результате длительность процесса регулирования будет меньше (см. переходную характеристику 2 на рисунке 3.18). Кратность корней характеристического уравнения утрачивается, поскольку они становятся комплексными. Все комплексные корни (и один вещественный при нечетном n) располагаются на одинаковом расстоянии h от оси мнимых чисел. Мнимые части корней образуют арифметическую прогрессию с разностью g и первым членом прогрессии также g. (3.19)
(3.19)
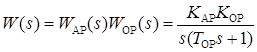




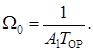
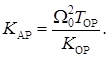


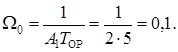



 ,
, .
.






 Кроме рассмотренных стандартных коэффициентов типовых ПФ вида (3.16) – (3.18) известны иные коэффициенты и соответствующие им оптимальные переходные характеристики h э(t), полученные с помощью интегральных критериев (см. п. 2.4.5.4). Названные коэффициенты и характеристики широко применяют при синтезе следящих приводов.
Кроме рассмотренных стандартных коэффициентов типовых ПФ вида (3.16) – (3.18) известны иные коэффициенты и соответствующие им оптимальные переходные характеристики h э(t), полученные с помощью интегральных критериев (см. п. 2.4.5.4). Названные коэффициенты и характеристики широко применяют при синтезе следящих приводов. в широком диапазоне частот. Поэтому электроприводы, настроенные по Баттерворту, называют настроенными на модульный оптимум (см. п. 2.5.10).
в широком диапазоне частот. Поэтому электроприводы, настроенные по Баттерворту, называют настроенными на модульный оптимум (см. п. 2.5.10).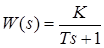 или
или 
 обозначен на комплексной плоскости (s ‑плоскости) знаком " ´ " (рисунок 3.22). Там же изображен КГ замкнутой системы, имеющий вид прямой линии. Основная ПФ системы согласно (2.32)
обозначен на комплексной плоскости (s ‑плоскости) знаком " ´ " (рисунок 3.22). Там же изображен КГ замкнутой системы, имеющий вид прямой линии. Основная ПФ системы согласно (2.32)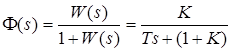 или
или 
 Очевидно, что при K = 0 полюсы разомкнутой и замкнутой САУ равны. При увеличении коэффициента усиления K единственный полюс замкнутой САУ
Очевидно, что при K = 0 полюсы разомкнутой и замкнутой САУ равны. При увеличении коэффициента усиления K единственный полюс замкнутой САУ  будет двигаться вдоль отрицательной вещественной полуоси. Траектория движения полюса согласно определению представляет собой корневой годограф. Стрелка указывает направление возрастания параметра K. Своим началом КГ имеет полюс разомкнутой САУ.
будет двигаться вдоль отрицательной вещественной полуоси. Траектория движения полюса согласно определению представляет собой корневой годограф. Стрелка указывает направление возрастания параметра K. Своим началом КГ имеет полюс разомкнутой САУ.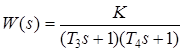 или
или 
 и
и  , которые на рисунке 3.23 также обозначены знаком " ´ ". Основная ПФ системы согласно (2.32)
, которые на рисунке 3.23 также обозначены знаком " ´ ". Основная ПФ системы согласно (2.32)
 Также очевидно, что при K = 0 полюсы разомкнутой и замкнутой САУ равны.
Также очевидно, что при K = 0 полюсы разомкнутой и замкнутой САУ равны.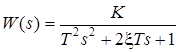
 (3.20)
(3.20)
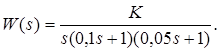
 Полюсы разомкнутой САУ p 1 = 0, p 2 = -10 и p 3 = -20 обозначены на комплексной плоскости знаком " ´ ".
Полюсы разомкнутой САУ p 1 = 0, p 2 = -10 и p 3 = -20 обозначены на комплексной плоскости знаком " ´ ".

 или
или  . (3.21)
. (3.21) Оценку качества скорректированной САУ проводят, как обычно, по переходной характеристике системы.
Оценку качества скорректированной САУ проводят, как обычно, по переходной характеристике системы.

 z ку = ‑10. В свою очередь полюс КУ p курасполагают вблизи от третьего полюса неизменяемой части системы p 3 = -20. Наилучшим положением p кусчитают такое, при котором КГ скорректированной САР проходит через доминирующие полюсы s 1, 2или в непосредственной близости от них (рисунок 3.28). Для исследуемой САР целесообразно принять полюс КУ p ку = -24. Наконец, коэффициент передачи K ку = 2,4 обеспечивает совместно с z ку = -10 и p ку = -24 заданные показатели качества скомпенсированной САУ t р = 0,65 и s = 25 %.
z ку = ‑10. В свою очередь полюс КУ p курасполагают вблизи от третьего полюса неизменяемой части системы p 3 = -20. Наилучшим положением p кусчитают такое, при котором КГ скорректированной САР проходит через доминирующие полюсы s 1, 2или в непосредственной близости от них (рисунок 3.28). Для исследуемой САР целесообразно принять полюс КУ p ку = -24. Наконец, коэффициент передачи K ку = 2,4 обеспечивает совместно с z ку = -10 и p ку = -24 заданные показатели качества скомпенсированной САУ t р = 0,65 и s = 25 %.
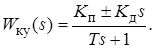

 ; K п = K д z ку = 1,0; T = 1/ p ку = 0,042.
; K п = K д z ку = 1,0; T = 1/ p ку = 0,042.


