
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Импликация. Необходимое и достаточное условия.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопросы на зачет по логике. 1. Виды и правила определения. Виды и правила деления. Импликация. Необходимое и достаточное условия. Структура, виды и правила доказательства. Структура, виды и правила опровержения. Законы тождества и достаточного основания. Законы непротиворечия и исключённого третьего. ПКС 1. Виды и правила определения. Определение (или дефиниция) понятия есть логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина. С помощью определения понятий мы в явной форме указываем на сущность отражаемых в понятии предметов, раскрываем содержание понятия и тем самым отличаем круг определяемых предметов от других предметов. 1. Явные и неявные определения. В явном определении понятие, содержание которого надо раскрыть, называется определяемым понятием [ definiendum (дефиниендум), сокращенно Dfd ], а то понятие, посредством которого оно определяется, называется определяющим понятием [ definience (дефиниенс), сокращенно — Dfn ]. Вотличие от явных определений, имеющих структуру 2. Реальные и номинальные определения Если определяется понятие, то определение будет реальным. Если определяется термин, обозначающий понятие, то определение будет номинальным. С помощью номинальных определений вводятся также новые термины, краткие имена взамен более сложных описаний предметов, знаки, заменяющие термины, раскрывается этимология того или иного термина. Для номинальных определений характерно присутствие в их составе слова «называют(ся)». Правила явного определения. Ошибки, возможные в определении 1. Определение должно быть соразмерным, т. е. объем определяющего понятия должен быть равен объему определяемого понятия. а) широкое определение, когда Dfd<Dfn. Такая ошибка содержится в определении: «Лошадь — млекопитающее и позвоночное животное». (Здесь понятие «лошадь» нельзя отличить от понятий «корова» или «коза».) б) узкое определение, когда Dfd>Dfh. Например, «Совесть — это осознание человеком ответственности перед самим собой за свои действия и поступки» (а перед обществом?). в) определение в одном отношениии широкое, в другом — узкое. В этих неправильных определениях Dfd>Dfn и Dfd<Dfn (в разных отношениях). Например, «Бочка — сосуд для хранения жидкостей». С одной стороны, это широкое определение, так как сосудом для хранения жидкостей может быть и чайник, и ведро, и т. д.; с другой стороны, это узкое определение, так как бочка пригодна для хранения и твердых тел, а не только жидкостей. 2. Определение не должно содержать круга. Круг возникает тогда, когда Dfd определяется через Dfn, a Dfn был определен через Dfd. В определении «Вращение есть движение вокруг своей оси» будет допущен круг, если до этого понятие «ось» было определено через понятие «вращение» («ось — это прямая, вокруг которой происходит вращение»). Круг возникает и тогда, когда определяемое понятие характеризуется через него же, лишь выраженное иными словами, или когда определяемое понятие включается в определяющее понятие в качестве его части. Такие определения носят название тавтологий. Тавтологичны такие определения: «Халатность заключается в том, что человек халатно относится к своим обязанностям». 3. Определение должно быть четким, ясным. Это правило означает, что смысл и объем понятий, входящих в Dfn, должен быть ясным и определенным. Определения понятий должны быть свободными от двусмысленности; не допускается подмена их - метафорами, сравнениями и т. д. Виды и правила деления. Деление — это логическая операция, посредством которой объем делимого понятия (множество) распределяется на ряд подмножеств с помощью избранного основания деления. Если с помощью определения понятия раскрывается его содержание, то с помощью деления понятия раскрывается его объем. Признак, по которому производится деление объема понятия, называется основанием деления. Подмножества, на которые разделен объем понятия, называются членами деления. Делимое понятие — это родовое, а его члены деления — это виды данного рода, соподчиненные между собой, т. е. не пересекающиеся по своему объему (не имеющие общих членов). Объем понятия можно делить по различным основаниям деления в зависимости от цели деления, от практических задач. Но при каждом делении на некотором его уровне должно браться лишь одно основание. Правила деления понятий 1. Соразмерность деления: объем делимого понятия должен быть равен сумме объемов членов деления. Например, Электрический ток делится на постоянный и переменный. Нарушение этого правила ведет к ошибкам двух видов: а) неполное деление, когда перечисляются не все виды данного родового понятия. «Энергия делится на механическую и химическую» (здесь нет, например, указания на электрическую энергию, атомную энергию). б) деление с лишними членами. Пример этого ошибочного деления: «Химические элементы делятся на металлы, неметаллы и сплавы». Лишний член («сплавы»), а сумма объемов понятий «металл» и «неметалл» исчерпывает объем понятия «химический элемент». 2. Деление должно проводиться только по одному основанию. Это означает, что нельзя брать два или большее число признаков, по которым бы производилось деление. Если будет нарушено это правило, то произойдет перекрещивание объемов понятий, которые появились в результате деления. (ошибка – подмена основания). 3. Члены деления должны исключать друг друга, т. е. не иметь общих элементов, быть соподчиненными понятиями, объемы которых не пересекаются. 4. Деление должно быть непрерывным, т. е. нельзя делать скачки в делении. Будет допущена ошибка, если мы скажем: «Сказуемые делятся на простые, на составные глагольные и составные именные». Правильным будет сначала разделить сказуемые на простые и составные, а затем уже составные сказуемые разделить на составные глагольные и составные именные. Классификация Классификация является разновидностью деления понятия, представляет собой вид последовательного деления и образует развернутую систему, в которой каждый ее член (вид) делится на подвиды и т. д. От обычного деления классификация отличается относительно устойчивым характером. Если классификация научна, то она сохраняется весьма длительное время. Классификация может производиться по существенным признакам (естественная) и по несущественным признакам (вспомогательная).
Определения как аргументы доказательства. 3. Аксиомы и постулаты. В математике, механике, теоретической физике, математической логике и других науках кроме определений вводят аксиомы. Аксиомы — это суждения, которые принимаются в качестве аргументов без доказательства. ПОНЯТИЕ ОПРОВЕРЖЕНИЯ
Опровержение — логическая операция установления ложности или необоснованности ранее выдвинутого тезиса. Опровержение должно показать, что: 1) неправильно построено само доказательство (аргументы или демонстрация); 2) выдвинутый тезис ложен или не доказан. Суждение, которое надо опровергнуть, называется тезисом опровержения. Суждения, с помощью которых опровергается тезис, называются аргументами опровержения. Существуют три способа опровержения: 1) опровержение тезиса (прямое и косвенное); 2) критика аргументов; 3) выявление несостоятельности демонстрации.
II. Критика аргументов Подвергаются критике аргументы, которые были выдвинуты оппонентом в обоснование его тезиса. Доказывается ложность или несостоятельность этих аргументов. Ложность аргументов не означает ложности тезиса: тезис может оставаться истинным.
Нельзя достоверно умозаключать от отрицания основания к отрицанию следствия. Но достаточно бывает показать, что тезис не доказан. Иногда бывает, что тезис истинен, но человек не может подобрать для его доказательства истинные аргументы.
Закон тождества Закон тождества является одним из законов правильного мышления, соблюдение этого закона гарантирует определенность и ясность мышления. Закон формулируется так: «В процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе». В математической логике закон тождества выражается следующими формулами:
Схема закона тождества: . В мышлении закон тождества выступает в качестве нормативного правила (принципа). Он означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. Нельзя тождественные мысли выдавать за различные, а различные — за тождественные. Нарушение закона тождества приводит к двусмысленности, что можно видеть, например, в следующих рассуждениях: «Ноздрев был в некотором отношении исторический человек. Ни на одном собрании, где он был, не обходилось без истории» (Н. В. Гоголь). Иногда в ходе дискуссий спор по существу подменяют спором о словах. Иногда люди говорят о разных вещах, думая, что они имеют в виду одного и того же человека либо одну и ту же вещь или событие. Логические ошибки часто совершают при употреблении омонимов, т. е. слов, имеющих два значения («следствие», «материя», «содержание» и др.). В результате отождествления различных понятий возникает логическая ошибка, называемая подменой понятия. При нарушении закона тождества возникает и другая ошибка, называемая подменой тезиса. В ходе доказательства или опровержения выдвинутый тезис часто умышленно или неосознанно подменяется другим. В научных и иных дискуссиях это проявляется в приписывании оппоненту того, чего он не говорил. Такие приемы ведения дискуссий недопустимы. Равенства обладают свойствами рефлексивности (а = а), симметричности (если а = b, то b = а)и транзитивности (если а = b и b = с, то а = с). К равенствам применимо правило замены равного равным. Различие также имеет свои виды и модификации: неравенство, неэквивалентность (неравномощность) множеств и т.д.; в теории алгоритмов — различие букв, неравенство конкретных слов (например, пустого и непустого слова) и др. Закон непротиворечия Если предмет А обладает определенным свойством, то в суждениях об А люди должны утверждать это свойство, а не отрицать его. Если же человек, утверждая что-либо, отрицает то же самое или утверждает нечто несовместимое с первым, налицо логическое противоречие. Формально-логические противоречия — это противоречия путаного, неправильного рассуждения. Такие противоречия затрудняют познание мира. Нельзя смешивать формально-логические противоречия с диалектическими. Закон единства и борьбы противоположностей действует всюду, поэтому диалектические противоречия свойственны природе, обществу и мышлению. Борьба противоположностей — движущая сила развития природы, общества и мышления. Аристотель считал «самым достоверным из всех начал» следующее: «...невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении»2. Тем самым Аристотель дал логическую формулировку закона непротиворечия: «Невозможно что-либо вместе утверждать и отрицать»3. Эта формулировка указывает на необходимость не допускать в своем мышлении и речи формально-противоречивые высказывания, в противном случае мышление будет неправильным. Мысль противоречива, если мы об одном и том же предмете в одно и то же время и в одном и том же отношении нечто и утверждаем, и отрицаем. Например, «Кама — приток Волги» и «Кама не является притоком Волги». Противоречия не будет, если мы говорим о разных предметах или об одном и том же предмете, взятом в разное время или в разном отношении. Противоречия не будет, если мы скажем: «Осенью дождь полезен для грибов» и «Осенью дождь не полезен для уборки урожая» Не могут быть одновременно истинными следующие четыре типа простых суждений: 1. «Данное S есть Р» и «Данное S не есть Р». 2. «Ни одно S не есть Р» и «Все S есть Р». 3. «Все S есть Р» и «Некоторые S не есть Р». 4. «Ни одно S не есть Р» и «Некоторые S есть Р». При этом вторая пара суждений такова, что оба суждения могут быть ложными, например: «Ни один студент не является спортсменом» и «Все студенты являются спортсменами». Формально-логическое противоречие чаще всего определяется как конъюнкция суждения и его отрицания (а и не-а). Но логическое противоречие может быть выражено и без отрицания; оно имеет место между несовместимыми утвердительными суждениями4. эмпириокритиками, с другой стороны, научными утверждениями естествоиспытателей. Формально-логическое противоречие возникает тогда, когда пытаются считать истинными два или несколько утвердительных суждений, не совместимых между собой. Не менее распространенной является форма логического противоречия, когда одновременно утверждается и отрицается одно и то же суждение, т. е. допускается конъюнкция а и не-а. Таким образом, в традиционной формальной логике противоречием считается утверждение двух противоположных (как контрарных, так и контрадикторных) суждений об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении. В исчислении высказываний классической двузначной логики закон непротиворечия записывается в виде формулы так: Закон непротиворечия читается так: «Два противоположных суждения не могут быть истинными в одно и то же время и в одном и том же отношении». К противоположным суждениям относятся: 1) противные (контрарные) суждения А и Е, которые оба могут быть ложными, поэтому не являются отрицающими друг друга и их нельзя обозначить как а и Формула закона непротиворечия в двузначной классической логике отражает лишь часть содержательного аристотелевского закона
Закон исключенного третьего В двузначной традиционной логике закон исключенного третьего формулируется так: «Из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано». Противоречащими (контрадикторными) называются такие два суждения, в одном из которых что-либо утверждается о предмете, а в другом то же самое об этом же предмете отрицается, поэтому они не могут быть оба истинными или оба ложными; одно из них истинно, а другое обязательно ложно. Такие суждения называются отрицающими друг друга. Если одно из противоречащих суждений обозначить переменной а, то другое следует обозначить а. Отрицающими являются следующие пары суждений:
1. «Это S есть Р» и «Это S не есть Р» (единичные суждения). 2. «Все S есть Р» и «Некоторые S не есть Р» (суждения А и О). 3. «Ни одно S не есть Р» и «Некоторые S есть Р» (суждения Е и I).
В отношении противоречащих (контрадикторных) суждений (А и О, Е и I) действует как закон исключенного третьего, так и закон непротиворечия — в этом одно из сходств данных законов. Различие в областях определения (применения) этих законов в том, что в отношении противных (контрарных) суждений А и Е (например, «Все грибы — съедобны» и «Ни один гриб не является съедобным»), которые не могут быть оба истинными, но могут быть оба ложными, действует лишь закон непротиворечия и не действует закон исключенного третьего. Поэтому сфера действия содержательного закона непротиворечия (контрарные и контрадикторные суждения) шире, чем сфера действия содержательного закона исключенного третьего (лишь контрадикторные суждения, т. е. суждения типа а и не-а). Действительно, истинно одно из двух суждений: «Все дома в данной деревне электрифицированы» или «Некоторые дома в данной деревне не; являются электрифицированными»; третьего не дано. Закон исключенного третьего и в содержательном, и в формализованном виде охватывает один и тот же круг суждений — противоречащие, т. е. отрицающие друг друга суждения. Содержательные аристотелевские законы непротиворечия и исключенного третьего невыводимы один из другого, так как области определения суждений, к которым они применимы, различны. В силу того что в формализованных законах непротиворечия и исключенного третьего, т. е. в формулах В мышлении закон исключенного третьего предполагает четкий выбор одной из двух взаимоисключающих альтернатив.
Категорический силлогизм — это вид дедуктивного умозаключения, в котором из двух истинных категорических суждений, где S и Р связаны средним термином, при соблюдении правил необходимо следует заключение. Силлогизм происходит от греческого syllogismos (сосчитывание, выведение следствия). В составе категорического силлогизма имеются две посылки и заключение.
Все металлы (М) электропроводны (Р) — большая посылка. Медь ( S) есть металл (М) — меньшая посылка. Медь (S) электропроводна (Р) — заключение.
Посылка, содержащая предикат заключения (т. е. больший термин), называется большей посылкой. Посылка, содержащая субъект заключения (т. е. меньший термин), называется меньшей посылкой. В основе вывода по категорическому силлогизму лежит аксиома силлогизма.
Особые правила фигур I фигура. Большая посылка должна быть общей, меньшая — утвердительной. II фигура. Большая посылка общая и одна из посылок, а также заключение отрицательные. III фигура. Меньшая посылка должна быть утвердительной, а заключение — частное. IV фигура. Общеутвердительных заключений не дает.
I. Правила терминов 1. В каждом силлогизме должно быть только три термина (S, Р, М). Ошибка называется «учетверение терминов». Ошибочное умозаключение:
Движение вечно. Хождение в институт — движение. ------------------------------------------ Хождение в институт вечно.
Здесь «движение» трактуется в разном смысле — в философском и обыденном. 2. Средний термин должен быть распределен по крайней мере в одной из посылок.
Некоторые растения (М) ядовиты (Р). Белые грибы (S) — растения (М). ------------------------------------------ Белые грибы (S) —- ядовиты (Р).
Здесь средний термин «растение» не распределен ни в одной из посылок, поэтому заключение ложное. 3. Термин распределен в заключении, если и только если он распределен в посылке. Иначе в терминах заключения говорилось бы больше, чем в терминах посылок.
Во всех городах за полярным кругом бывают белые ночи. Санкт-Петербург не находится за полярным кругом. ------------------------------------------- В Санкт-Петербурге не бывает белых ночей.
Заключение ложное, так как нарушено данное правило. Предикат вывода в заключении распределен, а в посылке он не распределен, следовательно, произошло расширение большего термина. II. Правила посылок 4. Из двух отрицательных посылок нельзя сделать никакого заключения. Например:
Дельфины не рыбы. Щуки не дельфины. ------------------------------------ ?
5. Если одна из посылок отрицательная, то и заключение должно быть отрицательным.
Все моржи — ластоногие. Это животное не является ластоногим. ------------------------------------- Это животное не является моржом.
6. Из двух частных посылок нельзя сделать заключение. Некоторые животные — пресмыкающиеся.
Некоторые живые организмы — животные. ----------------------------------------------- ?
7. Если одна из посылок частная, то заключение должно быть частным.
Все спекулянты подлежат наказанию. Некоторые люди — спекулянты. ------------------------------------------------ Некоторые люди подлежат наказанию.
Наиболее распространенные ошибки при умозаключении по категорическому силлогизму такие: 1. Заключение делается по I фигуре с меньшей отрицательной посылкой. Приведем два примера.
Все классные комнаты нуждаются в проветривании. Эта комната — не классная. ---------------------------------------- Эта комната не нуждается в проветривании.
Все студенты сдают экзамены. Смирнов не является студентом. ---------------------------------------- Смирнов не сдает экзамены.
Заключение не следует с необходимостью из посылок, так как вторая посылка должна быть утвердительной. 2. Заключение делается по II фигуре с двумя утвердительными посылками.
Все зебры полосатые. Это животное полосатое. -------------------------------- Это животное — зебра.
Заключение не следует с необходимостью из этих посылок, так как одна из посылок и заключение должны быть отрицательными суждениями.
Вопросы на зачет по логике. 1. Виды и правила определения. Виды и правила деления. Импликация. Необходимое и достаточное условия.
|
||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.25.4 (0.013 с.) |

 в неявных определениях просто на место Dfn подставляется контекст, или набор аксиом, или описание способа построения определяемого объекта. Бывают еще индуктивные неявные определения. Они характеризуются тем, что определяемый термин используется в выражении понятия, которое ему приписывается в качестве его смысла
в неявных определениях просто на место Dfn подставляется контекст, или набор аксиом, или описание способа построения определяемого объекта. Бывают еще индуктивные неявные определения. Они характеризуются тем, что определяемый термин используется в выражении понятия, которое ему приписывается в качестве его смысла Это правило часто нарушается, в результате, чего возникают логические ошибки в определении. Их типы:
Это правило часто нарушается, в результате, чего возникают логические ошибки в определении. Их типы:
 (в логике высказываний) и
(в логике высказываний) и 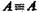 (в логике классов, в которой классы отождествляются с объемами понятий).
(в логике классов, в которой классы отождествляются с объемами понятий).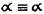 . Если в нее вместо
. Если в нее вместо  подставляются высказывания, то будет
подставляются высказывания, то будет 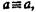 а если подставляются понятия, то будет
а если подставляются понятия, то будет 

 2) противоречащие (контрадикторные) суждения А и О, Е и /, а также единичные суждения «Это S есть Р» и «Это S не есть Р», которые являются отрицающими, так как если одно из них истинно, то другое обязательно ложно, поэтому их обозначают а и а.
2) противоречащие (контрадикторные) суждения А и О, Е и /, а также единичные суждения «Это S есть Р» и «Это S не есть Р», которые являются отрицающими, так как если одно из них истинно, то другое обязательно ложно, поэтому их обозначают а и а. непротиворечия, так как она относится только к противоречащим суждениям (а и не-а) и не распространяется на противные (контрарные) суждения. Поэтому формула
непротиворечия, так как она относится только к противоречащим суждениям (а и не-а) и не распространяется на противные (контрарные) суждения. Поэтому формула  неадекватно, не полностью представляет содержательный закон непротиворечия. Следуя традиции, мы сохраняем за формулой
неадекватно, не полностью представляет содержательный закон непротиворечия. Следуя традиции, мы сохраняем за формулой  название «закон непротиворечия», хотя оно значительно шире, чем формула. Если в мышлении (и речи) человека обнаружено формально-логическое противоречие, то такое мышление считается неправильным, а суждение, из которого вытекает противоречие, отрицается и считается ложным. Поэтому в полемике при опровержении мнения оппонента широко используется метод «приведения к абсурду».
название «закон непротиворечия», хотя оно значительно шире, чем формула. Если в мышлении (и речи) человека обнаружено формально-логическое противоречие, то такое мышление считается неправильным, а суждение, из которого вытекает противоречие, отрицается и считается ложным. Поэтому в полемике при опровержении мнения оппонента широко используется метод «приведения к абсурду». области определения пропозициональных переменных (т. е. переменных, обозначающих суждение и его отрицание:
области определения пропозициональных переменных (т. е. переменных, обозначающих суждение и его отрицание:  оказываются одними и теми же (берутся лишь противоречащие суждения), на основании закона де Моргана, т. е. формулы
оказываются одними и теми же (берутся лишь противоречащие суждения), на основании закона де Моргана, т. е. формулы 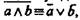 закона снятия двойного отрицания, т. е.
закона снятия двойного отрицания, т. е.  и закона коммуникативности дизъюнкции, т. е. формулы
и закона коммуникативности дизъюнкции, т. е. формулы  в двузначной классической логике путем элементарных эквивалентных преобразований из закона непротиворечия можно вывести закон исключенного третьего (и наоборот)
в двузначной классической логике путем элементарных эквивалентных преобразований из закона непротиворечия можно вывести закон исключенного третьего (и наоборот) 
 Понятия, входящие в состав силлогизма, называются терминами силлогизма. В приведенном примере терминами являются: Р («электропроводник») — больший термин, это предикат заключения; S («медь») — меньший термин, это субъект заключения; М («металл») — средний термин, служащий в посылках для связывания S и Р и отсутствующий в заключении (рис. 43).
Понятия, входящие в состав силлогизма, называются терминами силлогизма. В приведенном примере терминами являются: Р («электропроводник») — больший термин, это предикат заключения; S («медь») — меньший термин, это субъект заключения; М («металл») — средний термин, служащий в посылках для связывания S и Р и отсутствующий в заключении (рис. 43).


