
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка устойчивости верхней части колонныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Проверка устойчивости верхней части колонны в плоскости действия момента. Расчет на устойчивость внецентренно-сжатого элемента постоянного сечения в плоскости действия момента выполняем по формуле: N1/(φe*A0)≤Ry*γc, φe – коэффициент определяемый по табл. 74 СНиП II-23-81* и зависящий от условной гибкости mef x=η*mx, где η – коэффициент влияния формы сечения,определяемый по табл. 73 СНиП II-23-81*, mx=Mx/(N1*ρx) – относительный эксцентриситет. λx=lx2/ix=21600/291=74.2.
mx=765.853*103/(646.32*242)=4.90. Аf/Аw=5040/6640=0.76≈0.5. Коэффициент влияния формы сечения: η=(1,75-0,1*mx)-0,02*(5-mx)* η=(1,75-0,1*4.90)-0,02*(5-4.90)*2.53=1.26. mef x=1.26*4.90=6.15. По таблице 74 СНиП II-23-81* находим φe=0.173. σ=646.32/(0.173*240)=223.4 МПа < Ry=240 МПа. Недонапряжение: ∆=100*(240-223.4)/240=6.9 %. Проверка устойчивости верхней части колонны из плоскости действия момента. Расчет на устойчивость внецентренно-сжатых элементов постоянного сечения из плоскости действия момента выполняем по формуле: N1/(с*φy*A0)≤Ry*γc, где φy– коэффициент определяемый по табл. 72 СНиП II-23-81*. Определим коэффициенты с и φy. λy=ly2/iy=5400/63=86, по табл. 72 СНиП II-23-81* находим φy=0.640. Максимальный момент в средней трети расчетной длины стержня: Mx1/3=M2+(l2-ly2/3)*(M1-M2)/l2, Mx1/3=681.619+(7200-5400/3)*(-765.853-681.619)/7200=-404 кН*м. IMx1/3I>IМmax/2I=766/2=383 кН*м. Относительный эксцентриситет: mx=Mx1/3*A0/(N1*Wx), mx=-404*16720/(646.32*4045928)=2.58. При mx<5 коэффициент с, учитывающий влияние момента Мх при изгибно-крутильной форме, вычисляется по формуле: с=β/(1+α*mx), λy=86<λс=3.14*(E/Ry)0.5=3.14*(206000/240)0.5=92 => β=1, mx=2.58>1 => α=0,65+0,05*mx=0,65+0,05*2.58=0.78. c=1/(1+0.78*2.58)=0.33. Поскольку hw/tw=664/10=66.4<3.8*(E/Ry)0.5=3,8*(206000/240)0.5=111, то Aрасч=16720 мм2. σ=646.32/(0.33*0.640*16720)=182 МПа < Ry=240 МПа Недонапряжение: ∆=100*(240-182)/240=24.2 %. Подбор сечения нижней части колонны Выбор типа сечения нижней части колонны Сечение нижней части колонны сквозное, состоящее из двух ветвей, соединенных решеткой (рисунок 22). Высота сечения hн=1750 мм. Подкрановую ветвь колонны принимаем из горячекатаного двутавра с параллельными гранями полок по ГОСТ 26020-83, наружную – из составного сварного сечения из трех листов.
Рисунок 22. Сечение нижней части колонны Определим ориентировочное положение центра тяжести. Принимаем z0=57 мм, тогда расстояние между центрами тяжестей сечений ветвей: h0=h-z0, h0=1750-57=1693 мм. Положение центра тяжести найдем приближенно в предположении, что площади ветвей пропорциональны усилиям в них, тогда расстояние между центрами тяжести сечения подкрановой ветви и сечения всей колонны y1 и между центрами тяжести сечения наружной ветви и сечения всей колонны y2 равны:
y2=h0-y1. y1=2207.159*1693/(1986.137+2207.159)=891 мм; y2=1693-891=802 мм. Усилие в подкрановой ветви: Nв1=N3*y2/h0+M3/h0, Nв1=-3447.64*802/1693+(-1986.137)*103/1693=-2806.11 кН. Усилие в наружной ветви: Nв2=N4*y1/h0-M4/h0, Nв2=-3377.461*891/1693-2207.159*103/1693=-3081.44 кН. Требуемая площадь подкрановой ветви: Ав1=Nв1/(j*Ry), задаемся j=0.8; Ry=240 МПа. Ав1=2806.11*103/(0.8*240)=14615 мм2. Принимаем подкрановую ветвь – двутавр 60Б2 с параллельными гранями полок (ГОСТ 26020-83): Ав1=14730 мм2, ix1=49.2 мм, iy=243.9 мм, h=597 мм, b=230 мм, t=17.5 мм. Требуемая площадь наружной ветви: Ав2=Nв2/(j*Ry), задаемся j=0.737; Ry=240 МПа. Ав2=3081.44*103/(0.737*240)=17421 мм2, Для удобства прикрепления элементов решетки просвет между внутренними гранями полок принимаем таким же, как в подкрановой ветви (hвн=h-2*t=597-2*17.5=562 мм). Толщину стенки швеллера для удобства ее соединения встык с полкой надкрановой части колонны принимаем tw=18 мм; высота стенки из условия размещения сварных швов hw=650 мм. Тогда требуемая площадь полки: Af=(Aв2-tw*hw)/2, Af =(17421-18*650)/2=3960 мм2. Условие местной устойчивости полки швеллера: bсв/tf≤(0.36+0.1* Принимаем наружную ветвь – сварной швеллер с размерами: bf=220 мм, tf=18 мм (bсв/tf=12.2≤18), Af=3960 мм2, tw=18 мм, hw=650 мм, Aw=11700 мм2. Геометрические характеристики наружной ветви: Площадь сечениянаружной ветви: А в2=2*Аf+Аw, Ав2=2*3960+11700=19620 мм2. Расстояние между наружной гранью стенки швеллера и осью сечения швеллера: z0=[hw*tw*tw/2+2*Аf*(bf/2+tw)]/Ав2, z0=[650*18*18/2+2*3960*(220/2+18)]/19620=57 мм. Расстояние между осью стенкой швеллера и осью сечения швеллера: e=z0-0,5*tw, e=57-0,5*18=48 мм. Расстояние: c=tw+bf/2-z0, c=18+220/2-57=71 мм. Моменты инерции сечения наружной ветви относительно осей х2 и y: Ix2=2*tf*bf3/12+hw*tw*e2+2*bf*tf*c2, Iy=tw*hw3/12+2*tf*bf*((hвн+tw)/2)2. Ix2=2*18*2203/12+650*18*482+2*220*18*712=59504063 мм4. Iy=18*6503/12+2*18*220*((562+18)/2)2=1078009500 мм4. Радиусы инерции сечения наружной ветви относительно осeй х2 и y: ix2=(Ix2/Ав2)0,5, iy=(Iy/Ав2)0,5. ix2=(59504063/19620)0,5=55 мм, iy=(1078009500/19620)0,5=234 мм. Уточняем положение центра тяжести сечения колонны: h0=hн-z0=1750-57=1693 мм; y1=Ав2*h0/(Ав1+Ав2)=19620*1693/(14730+19620)=967 мм; y2=h0-y1=1693-967=726 мм. Уточняем усилия в ветвях колонны. Усилие в подкрановой ветви: Nв1=-3447.64*726/1693+(-1986.137)*103/1693=-2651.59 кН. Усилие в наружной ветви: Nв2=N4*y1/h0-M4/h0=-3377.461*967/1693-2207.159*103/1693=-3232.86 кН.
Рисунок 23. Сечение нижней части колонны
|
||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 796; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

 =λx*(Ry/E)0.5 и приведенного относительного эксцентриситета mеf определяемого по формуле:
=λx*(Ry/E)0.5 и приведенного относительного эксцентриситета mеf определяемого по формуле: <5
<5
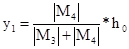 ,
,



