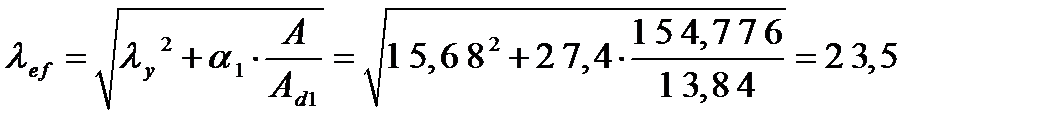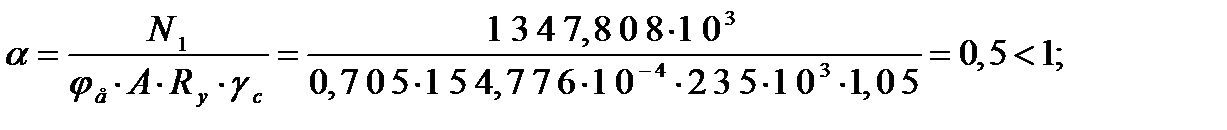Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка устойчивости подкрановой ветви колонны.Содержание книги Поиск на нашем сайте
40Б2 по ГОСТ 26021 Двутавры нормальные с параллельными гранями полок - Расчетная длина элемента lefx= 10150 мм; - Расчетная длина элемента lefy= 2337,5 мм; - Площадь A = 69,7 см 2= 69,7 / 0,01 = 6970 мм 2; - Момент инерции Jx= 18530 см 4= 18530 / 0,0001 = 185300000 мм 4; - Момент инерции Jy= 865 см 4= 865 / 0,0001 = 8650000 мм 4; - Момент сопротивления нетто Wx1= 935,7 см 3= 935,7 / 0,001 = 935700 мм 3; - Момент сопротивления нетто Wy1= 104,8 см 3= 104,8 / 0,001 = 104800 мм 3;
Радиус инерции: ix=; Jx/A=; 185300000/6970= 163,05019 мм.
Гибкость стержня относительно оси x: lx= lefx/ix= 10150/163,0502 = 62,25077.
Радиус инерции: iy=; Jy/A=; 8650000/6970= 35,2283 мм.
Гибкость стержня относительно оси y: ly= lefy/iy= 2337,5/35,2283 = 66,3529.
Гибкость: l = max(lx; ly) = max(62,25077;66,3529) = 66,3529.
Условная гибкость: l = l; Ry/E= 62,25077 ·; 235/210000= 2,08242.
Коэффициент продольного изгиба принимается по табл. Д.1 в зависимости от l f = 0,81281. a = N/(f A mkpRygc) = 1217000/(0,81281 · 6970 · 1 · 235 · 1,05) = 0,87059 < = 1 (87,05858 % от предельного значения) - условие выполнено (формула (7); п. 7.1.3).
Проверка по условию предельной гибкости сжатых элементов
По таблице 32 СП 16.13330.2010:
Тип элемента - 4. Основные колонны.
l = 62,25077 < = 180-60 a = 180-60 · 0,87059 = 127,7646 (48,72302 % от предельного значения) - условие выполнено.
Проверка устойчивости наружной ветви колонны.
Подберем сечения состоящее из 2 L 90x10 и листа 460x11 Геометрические характеристики:
Радиус инерции: ix=; Jx/A=; 201762000/8860= 150,9 мм.
Гибкость стержня относительно оси x: lx= lefx/ix= 10150/150,9 = 67,261.
Радиус инерции: iy=; Jy/A=; 6187120/8860= 26,426 мм.
Гибкость стержня относительно оси y: ly= lefy/iy= 2337,5/26,426 = 88,45.
Гибкость: l = max(lx; ly) = max(67,261; 88,45) = 88,45.
Условная гибкость: l = l; Ry/E= 88,45·; 235/210000= 2,96.
Коэффициент продольного изгиба принимается по табл. Д.1 в зависимости от l f = 0,568. a = N/(f A Rygc) = 1205200/(0,568 · 8860 · 235 · 1,05) = 0,97< = 1 (97 % от предельного значения) - условие выполнено (формула (7); п. 7.1.3).
Проверка по условию предельной гибкости сжатых элементов
По таблице 32 СП 16.13330.2010:
Тип элемента - 4. Основные колонны.
l = 88,45< = 180-60 a = 180-60 · 0,97 = 121,8 (72,619 % от предельного значения) - условие выполнено. Проверки устойчивости сечения в целом в плоскости рамы.
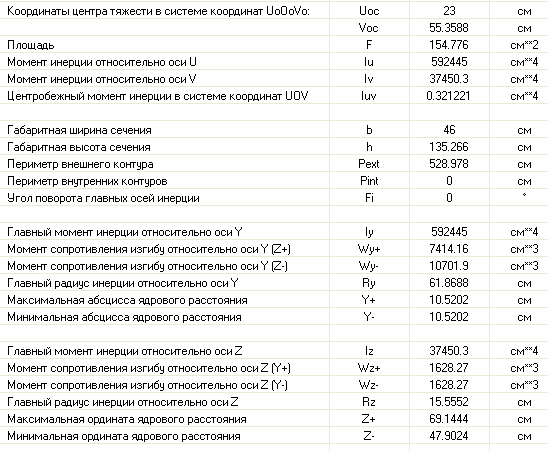
Геометрические характеристики сквозной колонны:
Расчет на сочетание нагрузок, догружающих подкрановую ветвь ( N1 = -1347.808 кН, М1 = -651.724 кНхм; ). Геометрические характеристики сечения:
Расстояние от главной оси сечения, перпендикулярной плоскости изгиба, до оси наиболее сжатой ветви, но не менее расстояния до оси стенки ветви: a = 125-(55,3588-2,01614) = 71,66 см. Относительный эксцентриситет приложения продольной силы:
Приведенная гибкость нижней части колонны:
где: α1 – коэффициент, принимаемый равным: Длина элемента решетки: d =; b 2+lb2=; 1,250 2+1,16875 2= 1,711 мм.
Аd1 =2∙6,92=13,84 см2 – площадь сечения решетки; λy – гибкость колонны без учета решетки,.
Условная приведенная гибкость нижней части колонны:
Коэффициент принимается по табл. Д.4 в зависимости от lefи m: fe= 0,705
Устойчивость нижней части колонны в плоскости рамы при загружении, подгружающем подкрановую ветвь, обеспечена. Проверка по условию предельной гибкости сжатых элементов
По таблице 32 СП 16.13330.2010: Тип элемента - 4. Основные колонны.
l = 15,68 < = 180-60 a = 180-60 · 0,5 = 150 (10 % от предельного значения) - условие выполнено.
|
||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |





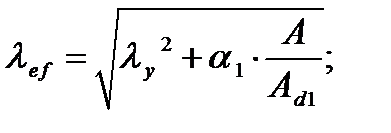
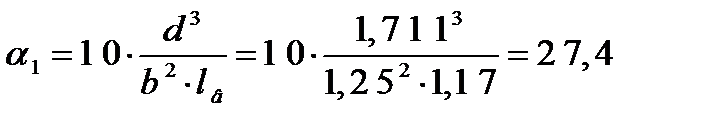 ;
;