Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подбор сечения нижней части колонныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нижняя часть колонны может выполняться сплошного или сквозного сечения. При высоте сечения колонны Колонна сквозного сечения При высоте сечения колонны На рис. 2.3 показан один из вариантов поперечного сечения внецентренно нагруженной колонны. Подкрановую ветвь колонны проектируют из прокатного двутавра. Наружную ветвь для удобства примыкания стеновых панелей компонуют из составного швеллера, (из двух равнобоких уголков и листа), либо выполняют из прокатного двутавра с параллельными гранями полок (по сортаменту ГОСТ 8239-89 или ГОСТ 26020-83). Колонна сквозного сечения при соединении ветвей с помощью уголковой решетки рассматривается как ферма с параллельными поясами. От действующих в колонне усилий M и N в ее ветвях возникают только продольные силы. Поперечная сила Q в сечениях колонны полностью воспринимается решеткой колонны. Несущая способность такой колонны может быть исчерпана в результате: - потери устойчивости какой-либо её ветвью (в плоскости или из плоскости рамы); - потери устойчивости колонны как единого стержня. Порядок расчета колонны сквозного сечения: а) определение расчетных усилий в ветвях колонны; б) подбор сечения подкрановой ветви колонны и проверка ее устойчивости из плоскости и в плоскости рамы; в) подбор сечения наружной ветви колонны и проверка ее устойчивости из плоскости и в плоскости рамы; г) расчет соединительной решетки ветвей колонны; д) проверка устойчивости колонны как единого стержня в плоскости рамы; е) проверка соотношений жесткостей (моментов инерции сечений) нижней и верхней частей колонны с полученными в результате статического расчета.
Рис. 2.3. К расчету колонны: а) конструктивная схема; б) сечение нижней части колонны а) Определение расчетных усилий в ветвях колонны Расчетные продольные усилия в наружной и подкрановой ветвях колонны ( В приведенном примере (табл. 1.10, 1.11) такими комбинациями усилий M и N являются: - для подкрановой ветви: - для наружной ветви: - для проверки устойчивости колонны как единого стержня
т. к. эта комбинация усилий дает максимальное значение суммы Поскольку сечение колонны несимметричное, необходимо определить положение центра тяжести сечения колонны (рис. 2.3).
Тогда расчетные значения усилий в ветвях колонны будут равны:
б) Подбор сечения подкрановой ветви колонны и проверка устойчивости принятого сечения Подкрановая ветвь колонны принимается из прокатного двутавра и рассчитывается на устойчивость как центрально сжатый стержень сначала из плоскости рамы (относительно оси y-y, рис. 2.3), а затем в плоскости рамы относительно оси Определяем ориентировочно требуемую площадь ветви колонны:
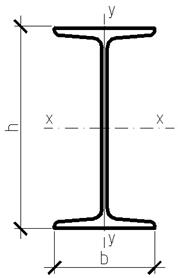
Рис. 2.4. Сечение подкрановой ветви колонны По требуемой площади поперечного сечения подкрановой ветви колонны подбираем соответствующий номер прокатного двутавра по таблицам 13, 14 Приложения и выписываем характеристики его сечения. Принимаем двутавр № 60: A = 138 см2, Ix = 78806 см4, Iу = 1725 см4, Wx = = 2560 см3, Wу = 182 см3, ix = 23,6 см, iy = 3,54 см.
Определяем гибкость принятого сечения подкрановой ветви колонны из плоскости рамы. Условная гибкость стержня Коэффициент устойчивости Предельно допустимая гибкость
Проверяем устойчивость подкрановой ветви колонны из плоскости рамы:
Устойчивость нижней части колонны зависит от назначаемого расстояния lв (рис. 2.3) между узлами присоединения элементов соединительной решетки к ветвям колонны. Тогда гибкость подкрановой ветви в плоскости рамы: Условная гибкость стержня Коэффициент устойчивости Предельно допустимая гибкость
Так как
Проверяем устойчивость подкрановой ветви колонны в плоскости рамы:
Проверки выполняются, однако сечение подобрано неэффективно – с запасом 35,3% прочности. Уменьшаем двутавр, принимаем двутавр № 50: A = 100 см2, Ix = 39727 см4, Iу = 1043 см4, ix = 19,9 см, iy = 3,23 см. Определяем гибкость принятого сечения подкрановой ветви колонны из плоскости рамы.
Условная гибкость стержня Коэффициент устойчивости
Проверяем устойчивость подкрановой ветви колонны из плоскости:
Проверка устойчивости принятого сечения двутавра в плоскости рамы.
Условная гибкость стержня Коэффициент устойчивости Проверяем устойчивость подкрановой ветви колонны в плоскости рамы:
Условия устойчивости подкрановой ветви колонны в плоскости и из плоскости рамы выполняется. в) Подбор сечения наружной ветви колонны Наружная ветвь колонны, как и подкрановая, рассчитывается как центрально сжатый стержень. Определяем ориентировочно требуемую площадь сечения ветви колонны.
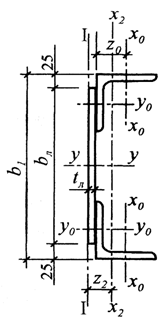
Наружная ветвь колонны принимается по сортаменту (т. 11, 12 Приложения) колонных двутавров с высотой сечения, равной принятому для подкрановой ветви. Порядок подбора сечения в этом случае аналогичен, как и для подкрановой ветви. Наружную ветвь колонны компонуем обычно из составного швеллера (рис. 1.6). Компонуем сечение наружной ветви колонны из листа по таблицам 16 а, 16 б Приложения и двух равнополочных уголков по таблице 17 Приложения (рис. 2.5) при условии, что их общая площадь сечения больше либо равна требуемой, определенной по формуле 2.33. Ширина листа bл принимается на 50 мм меньше высоты сечения двутавра подкрановой ветви.
Толщина листа tл принимается в пределах tл = (10…20) мм. Размеры листа подбирают так, чтобы площадь его сечения составила 50…60% требуемой площади ветви колонны. Для остальной части 40…50% требуемой площади сечения по сортаменту принимают два равнополочных уголка с возможно большей шириной полок (при минимальной их толщине). Выписываем из сортамента характеристики их сечения: площадь сечения – Ауг, момент инерции Jx и расстояние от обушка уголка до его центра тяжести
Рис. 2.5. Сечения наружной ветви колонны Принимаем лист с размерами сечения:
Определяем требуемую площадь поперечного сечения уголков:
Принимаем два равнополочных уголка 160х16: Aуг = 49,07 см2, Ix = 1175,19 см4, Определяем скомпонованную площадь сечения наружной ветви колонны:
Уточняем привязку оси Определяем моменты инерции сечения наружной ветви колонны относительно осей y и
Вычисляем радиусы инерции ветви колонны:
Определяем гибкости ветви колонны:
Проверяем устойчивость наружной ветви колонны: - из плоскости рамы
Коэффициент устойчивости - в плоскости рамы
Коэффициент устойчивости Проверки выполняются, однако сечение подобрано неэффективно с запасом 12,3% и 26,9% прочности. Уменьшаем толщину листа и сечение уголков. Принимаем лист с размерами сечения:
Принимаем два равнополочных уголка 160х14: Aуг = 43,57 см2, Ix = 1046,47 см4, z0 = 4,47 см. Определяем скомпонованную площадь сечения наружной ветви колонны:
Уточняем привязку оси x2 (рис. 1.4) наружной ветви колонны к её наружной грани:
Определяем моменты инерции сечения наружной ветви колонны относительно осей Y и X2::
Вычисляем радиусы инерции ветви колонны:
Определяем гибкости ветви колонны:
Проверяем устойчивость наружной ветви колонны: - из плоскости рамы
Принимаем - в плоскости рамы
Коэффициент устойчивости Условия выполняются, устойчивость наружной ветви колонны в плоскости и из плоскости рамы обеспечена.
г) Расчет соединительной решетки ветвей колонны Раскосы соединительной решетки воспринимают поперечную силу
Такая комбинация нагрузок обычно состоит из постоянной нагрузки и четырех переменных (снеговой, ветровой, а также вертикальной и боковой крановых). Расчет элементов соединительной решетки стержней составного сечения необходимо выполнить, как для элементов плоских ферм. Условная поперечная сила, приходящаяся на одну плоскость решетки:
Так как Для решетки (рис. 1.4.2. [1]) усилия в раскосе определяется по формуле:
Находим требуемую площадь сечения раскоса:
Исходя из требуемой площади раскоса, принимаем его сечение из равнополочного уголка. Из сортамента выписываем его площадь сечения Aр и радиус инерции imin (относительно оси у0 в сортаменте уголка). Принимаем равнополочный уголок 110х8: Ad = 17,20 см2, iy0 = 2,18 см. Определяем расчетную длину раскоса, гибкость раскоса и условную гибкость раскоса:
Коэффициент устойчивости Производим проверку устойчивости раскоса:
Проверка выполняется. Стойки соединительной решетки (рис. 2.3) рассчитываем на условную поперечную силу Определяем требуемый радиус инерции сечения стойки:
По значению требуемого радиуса инерции из сортамента выбираем равнобокий уголок при условии, что радиус инерции уголка
Принимаем равнополочный уголок № 50х5: А = 4,80 см; iy0 = 0,98 см.
Проверка выполняется. д) Проверка устойчивости нижней части колонны как единого стержня в плоскости рамы Определение геометрических характеристик всего сечения колонны (рис. 2.3): - площадь всего сечения колонны
- момент инерции сечения колонны относительно оси Х-Х
Момент инерции - радиус инерции сечения колонны
Находим гибкость стержня колонны относительно свободной оси Х-Х: (рис. 1.3)
Тогда приведенная гибкость стержня колонны с учетом податливости решетки по таблице 18 Приложения (табл. 1.4.2., [1]):
Определяем условную приведенную гибкость колонны:
Вычисляем относительный эксцентриситет для комбинации усилий, вызывающих наибольшее сжатие в одной из ветвей колонны. Обычно наиболее сжатой ветвью является наружная ветвь колонны (см. табл. 1.10, 1.11 Приложения). По этой комбинации усилий Mн и Nн производим определение относительного эксцентриситета mx и проверку устойчивости сечения колонны в целом. Относительный эксцентриситет для наружной ветви колонны находим по формуле:
Затем производим проверку устойчивости колонны как единого стержня в плоскости рамы:
Для
Условие устойчивости колонны как единого сжатого стержня в плоскости рамы выполнено.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.105.80 (0.012 с.) |

 ее обычно выполняют сплошного сечения, которое может быть либо симметричного вида – из составного двутавра, составленного из трех листов, либо несимметричного вида – рис. 1.6. Расчет нижней части колонны сплошного сечения производится аналогично приведенному выше для верхней части колонны.
ее обычно выполняют сплошного сечения, которое может быть либо симметричного вида – из составного двутавра, составленного из трех листов, либо несимметричного вида – рис. 1.6. Расчет нижней части колонны сплошного сечения производится аналогично приведенному выше для верхней части колонны.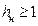 ее выполняют сквозного сечения, состоящей из двух ветвей, связанных между собой решеткой.
ее выполняют сквозного сечения, состоящей из двух ветвей, связанных между собой решеткой.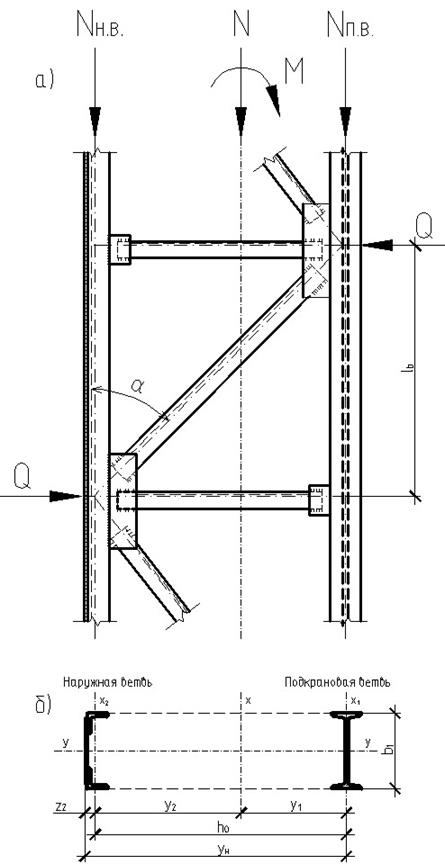
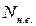 и
и  ) находим из полученных комбинаций усилий M и N в сечениях колонны, для которых значение суммы
) находим из полученных комбинаций усилий M и N в сечениях колонны, для которых значение суммы  наибольшим (см. табл.1.10, 1.11).
наибольшим (см. табл.1.10, 1.11).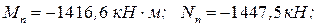
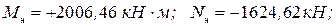

 .
.
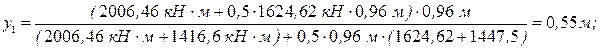
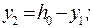
 -
-

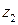 сначала принимается ориентировочно равным 3…4 см, а при сечении наружной ветви из прокатного двутавра – 10 см);
сначала принимается ориентировочно равным 3…4 см, а при сечении наружной ветви из прокатного двутавра – 10 см);
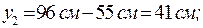

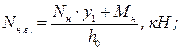
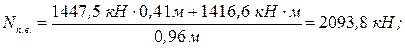
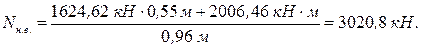
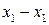 .
.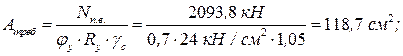
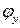 -
-
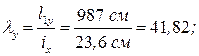
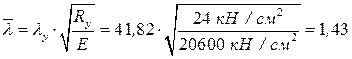 . Определяем тип кривой устойчивости по таблице 15 Приложения (т. 1.4.1, [1]) - «b».
. Определяем тип кривой устойчивости по таблице 15 Приложения (т. 1.4.1, [1]) - «b». определяется интерполяцией по таблице 11 Приложения (т. К.1, Приложения [1]). Для
определяется интерполяцией по таблице 11 Приложения (т. К.1, Приложения [1]). Для 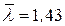 и типа кривой устойчивости «b», интерполируя
и типа кривой устойчивости «b», интерполируя 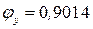 .
.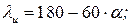
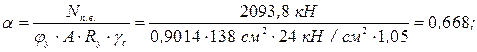
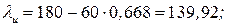
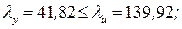
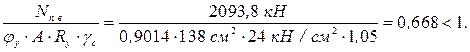

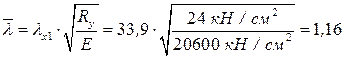 .
.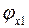 определяется интерполяцией по т. 11 Приложения (т. К.1, Приложения [1]). Для
определяется интерполяцией по т. 11 Приложения (т. К.1, Приложения [1]). Для 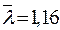 и типа кривой устойчивости «b», интерполируя
и типа кривой устойчивости «b», интерполируя  .
.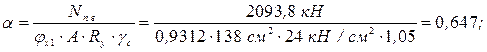
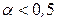 , принимаем
, принимаем 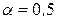 .
.
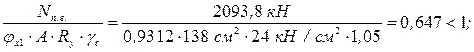
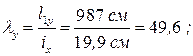
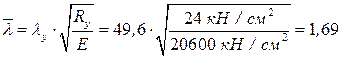 .
.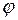 определяется интерполяцией по таблице 11 Приложения (т. К.1, Приложения [1]). Для
определяется интерполяцией по таблице 11 Приложения (т. К.1, Приложения [1]). Для  и типа кривой устойчивости «b» принимаем, интерполируя,
и типа кривой устойчивости «b» принимаем, интерполируя,  .
.
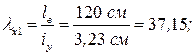
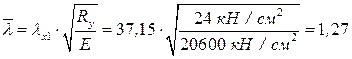 .
.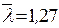 и типа кривой устойчивости «b» принимаем, интерполируя,
и типа кривой устойчивости «b» принимаем, интерполируя,  .
.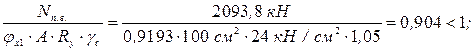

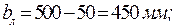
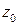 .
.

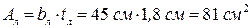
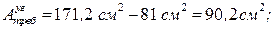
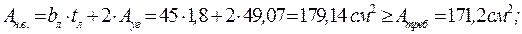

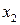 (рис. 2.5) наружной ветви колонны к её наружной грани:
(рис. 2.5) наружной ветви колонны к её наружной грани: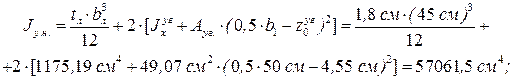
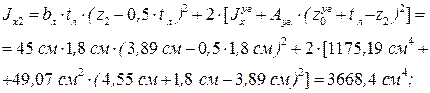
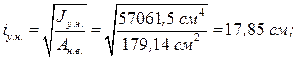
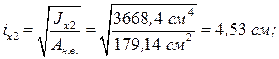


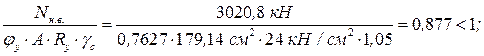
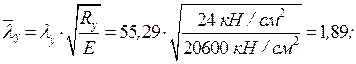
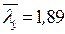 и типа кривой устойчивости «c» принимаем, интерполируя,
и типа кривой устойчивости «c» принимаем, интерполируя, 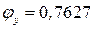 .
.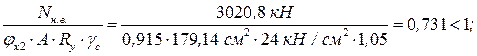

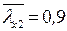 и типа кривой устойчивости «c» принимаем, интерполируя,
и типа кривой устойчивости «c» принимаем, интерполируя, 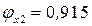 .
.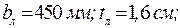
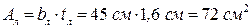
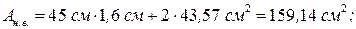

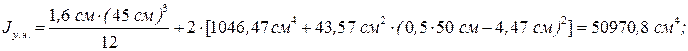
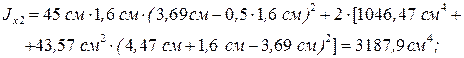




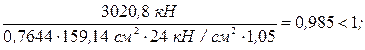
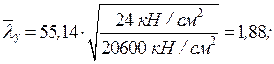
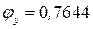 .
.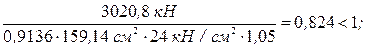
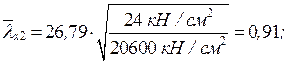
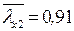 и типа кривой устойчивости «c» принимаем, интерполируя,
и типа кривой устойчивости «c» принимаем, интерполируя,  .
.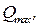 значение которой определяется по табл. 1.9 в сечении 1-1 колонны. Для этого выбираем комбинацию нагрузок, при которой поперечная сила в колонне будет максимальной.
значение которой определяется по табл. 1.9 в сечении 1-1 колонны. Для этого выбираем комбинацию нагрузок, при которой поперечная сила в колонне будет максимальной. -
-
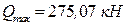 ;
;
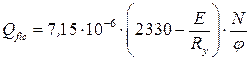
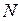 -
-
 ;
;
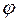 -
-
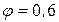 ;
;
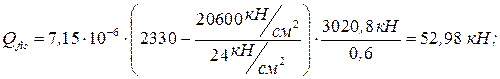
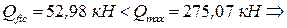 подбор элементов решетки выполняем по
подбор элементов решетки выполняем по 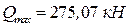 .
.
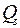 -
-
 ;
;
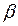 -
-
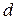 -
-
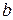 -
-
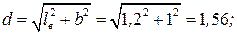

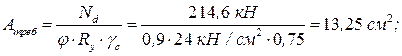
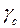 -
-
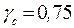 ;
;
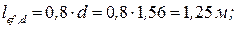

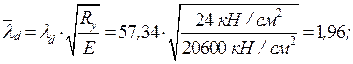
 и типа кривой устойчивости «c» принимаем, интерполируя,
и типа кривой устойчивости «c» принимаем, интерполируя, 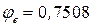 .
.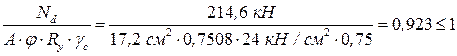
 .
.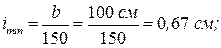


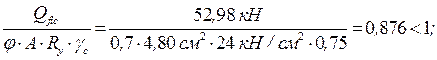
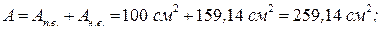

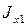 равняется моменту инерции подкрановой ветви
равняется моменту инерции подкрановой ветви 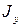 .
.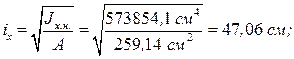
 -
-
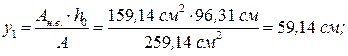
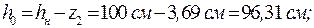
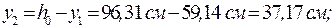

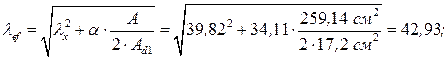
 -
-

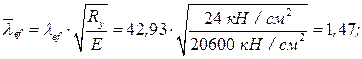
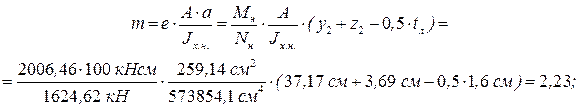
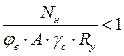
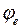 -
-
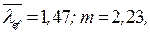 принимаем, интерполируя,
принимаем, интерполируя, 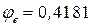 .
.