
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение в сети встречного распространенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Возможности сети встречного распространения, разработанной в [5-7], превосходят возможности однослойных сетей. Время же обучения по сравнению с обратным распространением может уменьшаться в сто раз. Встречное распространение не столь общо, как обратное распространение, но оно может давать решение в тех приложениях, где долгая обучающая процедура невозможна. Будет показано, что помимо преодоления ограничений других сетей встречное распространение обладает собственными интересными и полезными свойствами. Во встречном распространении объединены два хорошо известных алгоритма: самоорганизующаяся карта Кохонена [8] и звезда Гроссберга [2-4] (см. приложение Б). Их объединение ведет к свойствам, которых нет ни у одного из них в отдельности. Методы, которые подобно встречному распространению, объединяют различные сетевые парадигмы как строительные блоки, могут привести к сетям, более близким к мозгу по архитектуре, чем любые другие однородные структуры. Похоже, что в мозгу именно каскадные соединения модулей различной специализации позволяют выполнять требуемые вычисления. Сеть встречного распространения функционирует подобно столу справок, способному к обобщению. В процессе обучения входные векторы ассоциируются с соответствующими выходными векторами. Эти векторы могут быть двоичными, состоящими из нулей и единиц, или непрерывными. Когда сеть обучена, приложение входного вектора приводит к требуемому выходному вектору. Обобщающая способность сети позволяет получать правильный выход даже при приложении входного вектора, который является неполным или слегка неверным. Это позволяет использовать данную сеть для распознавания образов, восстановления образов и усиления сигналов. СТРУКТУРА СЕТИ На рис. 4.1 показана упрощенная версия прямого действия сети встречного распространения. На нем иллюстрируются функциональные свойства этой парадигмы. Полная двунаправленная сеть основана на тех же принципах, она обсуждается в этой главе позднее.
Рис. 4.1. Сеть с встречным распознаванием без обратных связей Нейроны слоя 0 (показанные кружками) служат лишь точками разветвления и не выполняют вычислений. Каждый нейрон слоя 0 соединен с каждым нейроном слоя 1 (называемого слоем Кохонена) отдельным весом w mn. Эти веса в целом рассматриваются как матрица весов W. Аналогично, каждый нейрон в слое Кохонена (слое 1) соединен с каждым нейроном в слое Гроссберга (слое 2) весом v np. Эти веса образуют матрицу весов V. Все это весьма напоминает другие сети, встречавшиеся в предыдущих главах, различие, однако, состоит в операциях, выполняемых нейронами Кохонена и Гроссберга.
Как и многие другие сети, встречное распространение функционирует в двух режимах: в нормальном режиме, при котором принимается входной вектор Х и выдается выходной вектор Y, и в режиме обучения, при котором подается входной вектор и веса корректируются, чтобы дать требуемый выходной вектор. НОРМАЛЬНОЕ ФУНКЦИОНИРОВАНИЕ Слои Кохоненна В своей простейшей форме слой Кохонена функционирует в духе «победитель забирает все», т. е. для данного входного вектора один и только один нейрон Кохонена выдает на выходе логическую единицу, все остальные выдают ноль. Нейроны Кохонена можно воспринимать как набор электрических лампочек, так что для любого входного вектора загорается одна из них. Ассоциированное с каждым нейроном Кохонена множество весов соединяет его с каждым входом. Например, на рис. 4.1 нейрон Кохонена К 1 имеет веса w 11, w 21, …, w m1, составляющие весовой вектор W 1. Они соединяются-через входной слой с входными сигналами х 1, x 2, …, x m, составляющими входной вектор X. Подобно нейронам большинства сетей выход NET каждого нейрона Кохонена является просто суммой взвешенных входов. Это может быть выражено следующим образом: NETj = w 1j x 1 + w 2j x 2 + … + w mj x m (4.1) где NETj – это выход NET нейрона Кохонена j,
или в векторной записи N = XW, (4.3) где N – вектор выходов NET слоя Кохонена. Нейрон Кохонена с максимальным значением NET является «победителем». Его выход равен единице, у остальных он равен нулю. Слой Гроссберга Слой Гроссберга функционирует в сходной манере. Его выход NET является взвешенной суммой выходов k 1, k 2,..., k n слоя Кохонена, образующих вектор К. Вектор соединяющих весов, обозначенный через V, состоит из весов v 11, v 21,..., v np. Тогда выход NET каждого нейрона Гроссберга есть
где NETj – выход j -го нейрона Гроссберга, или в векторной форме
Y = KV, (4.5) где Y – выходной вектор слоя Гроссберга, К – выходной вектор слоя Кохонена, V – матрица весов слоя Гроссберга. Если слой Кохонена функционирует таким образом, что лишь у одного нейрона величина NET равна единице, а у остальных равна нулю, то лишь один элемент вектора К отличен от нуля, и вычисления очень просты. Фактически каждый нейрон слоя Гроссберга лишь выдает величину веса, который связывает этот нейрон с единственным ненулевым нейроном Кохонена. ОБУЧЕНИЕ СЛОЯ КОХОНЕНА Слой Кохонена классифицирует входные векторы в группы схожих. Это достигается с помощью такой подстройки весов слоя Кохонена, что близкие входные векторы активируют один и тот же нейрон данного слоя. Затем задачей слоя Гроссберга является получение требуемых выходов. Обучение Кохонена является самообучением, протекающим без учителя. Поэтому трудно (и не нужно) предсказывать, какой именно нейрон Кохонена будет активироваться для заданного входного вектора. Необходимо лишь гарантировать, чтобы в результате обучения разделялись несхожие входные векторы. Предварительная обработка входных векторов Весьма желательно (хотя и не обязательно) нормализовать входные векторы перед тем, как предъявлять их сети. Это выполняется с помощью деления каждой компоненты входного вектора на длину вектора. Эта длина находится извлечением квадратного корня из суммы квадратов компонент вектора. В алгебраической записи
Это превращает входной вектор в единичный вектор с тем же самым направлением, т. е. в вектор единичной длины в n-мерном пространстве. Уравнение (4.6) обобщает хорошо известный случай двух измерений, когда длина вектора равна гипотенузе прямоугольного треугольника, образованного его х и у компонентами, как это следует из известной теоремы Пифагора. На рис. 4.2а такой двумерный вектор V представлен в координатах х-у, причем координата х равна четырем, а координата y – трем. Квадратный корень из суммы квадратов этих компонент равен пяти. Деление каждой компоненты V на пять дает вектор V с компонентами 4/5 и 3/5, где V ’ указывает в том же направлении, что и V, но имеет единичную длину. На рис. 4.26 показано несколько единичных векторов. Они оканчиваются в точках единичной окружности (окружности единичного радиуса), что имеет место, когда у сети лишь два входа. В случае трех входов векторы представлялись бы стрелками, оканчивающимися на поверхности единичной сферы. Эти представления могут быть перенесены на сети, имеющие произвольное число входов, где каждый входной вектор является стрелкой, оканчивающейся на поверхности единичной гиперсферы (полезной абстракцией, хотя и не допускающей непосредственной визуализации).
Рис. 4.2а. Единичный входной вектор
Рис. 4.26. Двумерные единичные векторы на единичной окружности При обучении слоя Кохонена на вход подается входной вектор и вычисляются его скалярные произведения с векторами весов, связанными со всеми нейронами Кохонена. Нейрон с максимальным значением скалярного произведения объявляется «победителем» и его веса подстраиваются. Так как скалярное произведение, используемое для вычисления величин NET, является мерой сходства между входным вектором и вектором весов, то процесс обучения состоит в выборе нейрона Кохонена с весовым вектором, наиболее близким к входному вектору, и дальнейшем приближении весового вектора к входному. Снова отметим, что процесс является самообучением, выполняемым без учителя. Сеть самоорганизуется таким образом, что данный нейрон Кохонена имеет максимальный выход для данного входного вектора. Уравнение, описывающее процесс обучения имеет следующий вид:
w н = w с + a(x – w с), (4.7) где w н – новое значение веса, соединяющего входную компоненту х с выигравшим нейроном; w с – предыдущее значение этого веса; a – коэффициент скорости обучения, который может варьироваться в процессе обучения. Каждый вес, связанный с выигравшим нейроном Кохонена, изменяется пропорционально разности между его величиной и величиной входа, к которому он присоединен. Направление изменения минимизирует разность между весом и его входом. На рис. 4.3 этот процесс показан геометрически в двумерном виде. Сначала находится вектор X – W с, для этого проводится отрезок из конца W в конец X. Затем этот вектор укорачивается умножением его на скалярную величину a, меньшую единицы, в результате чего получается вектор изменения δ. Окончательно новый весовой вектор W н является отрезком, направленным из начала координат в конец вектора δ. Отсюда можно видеть, что эффект обучения состоит во вращении весового вектора в направлении входного вектора без существенного изменения его длины.
Рис. 4.3. Вращение весового вектора в процессе обучения (Wн – вектор новых весовых коэффициентов, Wс – вектор старых весовых коэффициентов) Переменная к является коэффициентом скорости обучения, который вначале обычно равен ~ 0,7 и может постепенно уменьшаться в процессе обучения. Это позволяет делать большие начальные шаги для быстрого грубого обучения и меньшие шаги при подходе к окончательной величине. Если бы с каждым нейроном Кохонена ассоциировался один входной вектор, то слой Кохонена мог бы быть обучен с помощью одного вычисления на вес. Веса нейрона-победителя приравнивались бы к компонентам обучающего вектора (a = 1). Как правило, обучающее множество включает много сходных между собой входных векторов, и сеть должна быть обучена активировать один и тот же нейрон Кохонена для каждого из них. В этом случае веса.этого нейрона должны получаться усреднением входных векторов, которые должны его активировать. Постепенное уменьшение величины a уменьшает воздействие каждого обучающего шага, так что окончательное значение будет средней величиной от входных векторов, на которых происходит обучение. Таким образом, веса, ассоциированные с нейроном, примут значение вблизи «центра» входных векторов, для которых данный нейрон является «победителем».
|
||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.011 с.) |


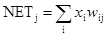 (4.2)
(4.2) , (4.4)
, (4.4) (4.6)
(4.6)





