
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уровни варьирования значений факторовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Минимальные и максимальные значения факторов приняты следующие:
Среднее значение фактора Среднее значение фактора определяется по формуле:
X10 = ______________________; X20 = ______________________; X30 = ______________________.
Интервалы варьирования фактора Интервал варьирования определяется по формуле:
dx1 = X10 – X1min = _________________________. dx2 = X20 – X2min = __________________________. dx3 = X30 – X3min = __________________________.
6. Корректность определения значений факторов
Нормированные значения факторов Нормированные значения определяются формулой:
Хн1 = _____________________; Хн2 = _____________________; Хн3= _____________________.
8. Матрица планирования полного факторного эксперимента Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен и равен 1.
Экспериментальные значения целевой функции
9. Дисперсия среднего арифметического для каждой строки матрицы эксперимента (каждого опыта) Дисперсия среднего арифметического определяется формулой:
где m – количество параллельных опытов в строке матриц.
Расчетное значение критерия Кохрена Критерий Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них, и определяется по формуле:
где S2max – наибольшая величина дисперсии результатов опыта; si – дисперсия i-го опыта$ N – общее число опытов в матрице. Максимальное значение дисперсии результатов опыта:
S2ymax= __________ = __________. Сумма всех построчных дисперсий:
Расчетное значение критерия Кохрена:
Gp=
В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N, где N – число опытов (количество строк в матрице планирования). Табличное значение критерия Кохрена Уровень значимости.
a = ______.
Степень числителя (f1):
f1= m –1= ________,
где m – количество параллельных опытов в строке матриц
Степень свободы знаменателя (f2):
f2 = N = ______,
где N – общее число опытов в матрице. Табличное значение критерия Кохрена
Gт = _________. Оценка однородности дисперсии результатов опыта.
Так как расчётное значение Gp, которое равно ________, меньше табличного значения Gт, которое равно 0,4251, то соблюдается условие:
Gт > Gp,
Следовательно с достоверностью 1 – a, т.е _______ все построчные дисперсии являются однородными.
Вид уравнения регрессии, принятого для построения модели функции отклика
Рекомендуется полиномиальная модель функции отклика
y = ______________________________________________________.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.186.233 (0.007 с.) |

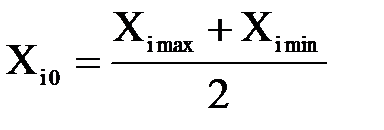 .
. .
.

 S2 y = ________________________________________________ = _____.
S2 y = ________________________________________________ = _____. _______.
_______.


