
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия интервального рядаСодержание книги Поиск на нашем сайте
Дисперсия – (определение). Дисперсия может быть рассчитана по формуле:
D =
где _________________________.
Расчетные значения приведены в таблице 7
Таблица 7 – Расчет дисперсии ряда
D =
Среднее квадратическое отклонение
Среднее квадратическое отклонение – (определение). Среднее квадратическое отклонение рассчитывается по формуле:
σ =
Коэффициент вариации Коэффициент вариации определяется по формуле:
δ =
где ____________________________.
Характеристики описательной статистики
Средствами программы Excel рассчитаны характеристики описательной статистики заданного ряда, числовые значения которых приведены на рисунке 5.
Рисунок 5 – Характеристики описательной статистики
Вывод. ________________________________________________________
Задача 2. Статистический анализ двумерной последовательности случайных величин Цель работы. Освоить компетенции выполнения статистического анализа двумерных данных, выявить зависимость (связь) между случайными величинами. Взаимосвязь может быть оценена следующими методами: 1) Визуальный метод 2) Корреляционный анализ 3) Регрессионный анализ
Исходные данные
В качестве исходных данных принято двух последовательных случайных величин: первая - _______________________________________________; вторая - ______________________________________________ Исходные данные представлены в таблице 1.
Таблица 1 – Исходные данные
Примем: в качестве аргумента Xi - __________________________; в качестве функции Yi - __________________________.
Визуальный анализ
Определение метода анализа
По данным таблицы 1 построен точечный график (рис. 1).
Рисунок 1 – Точечный график
Корреляционный анализ
Корреляционная зависимость – (определение). Корреляционный анализ выполнен с помощью пакета «Анализ данных» программы Excel, результаты которого показаны в таблице 2.
Таблица 2 - результаты корреляционного анализа
Вывод: _________________________________________________
Регрессионный анализ
Регрессионный анализ – (определение). Регрессионный анализ заданных последовательностей выполнен с помощью режима Регрессия пакета «Анализ данных» программы MS Excel. Сгенерируются результаты по регрессионной статистике, представленные в таблице 3.
Таблица 3- Результаты регрессионного анализа
Расчитанные в таблицах характеристики представляют собой: Дать описание приведенных в таблицах характеристик.
Регрессионные модели
Построение регрессионных моделей выполнено с помощью команды «Построение линии тренда» программы Excel. На нижеприведенных рисунках показаны различные регрессионные модели, описывающие связь между двумя заданными последовательностями случайных величин.
Рисунок 2 – Экспоненциальная модель
Рисунок 3 – Линейная модель
Рисунок 4 – Логарифмическая модель
Рисунок 5 – Полиномиальная модель
Рисунок 6 – Полиномиальная модель
В таблице 3 показаны сводные данные по всем построенным моделям.
Вывод: _______________________________________________
Заключение
________________________________________________________
Часть 2 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
1. Реалистичное содержание целевой функции В качестве целевой функции (функции отклика, зависимой переменной, реакции системы на воздействие факторов Xi) Y принята _______________:
Y = f(Х1, Х2, Х3).
2. Реалистичное содержание (сущность) факторов
В качестве факторов функции отклика Xi принимаются:
X1 - _______________________________; X2 - _______________________________; Х3 - _______________________________.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.199 (0.006 с.) |


 ____________.
____________. = _______ = _______.
= _______ = _______.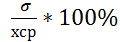 = ________= ______.
= ________= ______.




