
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 1. Статистический анализ одномерной последовательности случайных величинСодержание книги
Поиск на нашем сайте
Цель работы: приобрести компетенции статистического анализа одномерной последовательности случайных величин. Задание: 1. Подготовить исходные данные. 2. Построить вариационный, статистический, группированный ряды. 3. Построить гистограмму, полигон, кумуляту, огиву. 4. Определить относительные частоты последовательности. 5. Определить: среднее арифметическое (по вариационному ряду), средневзвешенное (по группированному ряду), моду, медиану, дисперсию (по группированному ряду); среднее квадратическое отклонение, коэффициент вариации. 6. Рассчитать в программе Excel характеристики описательной статистики для заданной последовательности случайных величин.
Исходные данные
В качестве исходных данных принята [ числовые характеристики из нефтегазовой сферы ] (табл. 1).
Таблицы 1- Наименование случайной величины, е.и.
Вариационный ряд Вариационный ряд – (определение) Для заданной последовательности случайных величин вариационный ряд показан в (таблица 2).
Таблица 2- Вариационный ряд для _____________________________
Характеристиками вариационного ряда: - максимальное значение ряда Хmax = ______; - минимальное значение ряда Xmin = ______; - размах ряда R = Xmax – Xmin = _________.
Статистического ряда
Статистический ряд - – (определение). Для заданной последовательности случайных величин вариационный ряд показан в таблице 3.
Таблица 3- Статистический ряд случайных величин, k
Построение группированного (интервального) ряда
Группированный ряд – (определение). Для построения группированного ряда принято t = ______ интервалов. Ширина интервалов оправляются по формуле:
rt = R/t + Δt,
где - R – размах вариационного ряда; t – количество интервалов; Δ – малая величина, позволяющая исключить повтор границ интервалов (рекомендуется назначить равной 0,1% от размаха интервала).
Таблица 4 – Значения границ интервалов
Интервальный ряд представлен в таблице 5.
Таблица 5 - Группированный ряд
Гистограмма Гистограмма - (определине). Гистограмма построена по средним значениям группированного ряда (рис. 1)
Рисунок 1 - Гистограмма
Полигон
Полигон – (определение). Полигон показан на рисунке 2.
Рисунок 2 - Полигон
Кумулята Кумулята – (определение). Кумулята показан на рисунке 3.
Рисунок 3 - Кумулята Огива
Огива – (определение). Огива показан на рисунке 4.
Рисунок 4 – Огива
Объем выборки
Объём выборки определяется по формуле (3):
N=
где: ______________.
Относительные частоты
Относительная частота определяется по формуле:
W = ni/n = ____________________ = _________,
где ________________.
Значения относительных частот приведены в таблице 6.
Таблица 6- Расчет относительный частот
11. Среднее арифметическое:
Среднее арифметическое ряда определяется по формуле:
X=
Средневзвешенное значение статистического ряда определяется по формуле:
X=
где _______________________________.
Мода
Мода – (определение). Мода может быть определена по группированному ряду и для заданного ряда случайных величин имеет значение:
M = __________.
Медиана
Медианой называется – (определение). Медиана для заданного ряда имеет значение:
Me = ______ = ______.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.54.188 (0.009 с.) |




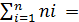 ___________________________.= _________,
___________________________.= _________,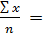 _______________ = ___________,
_______________ = ___________,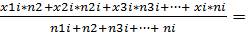 ______________________ = _____,
______________________ = _____,


