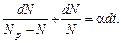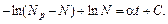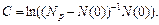Нелинейность математических моделей

В ряде случаев в научной и учебной литературе для упрощения ограничиваются преимущественно линейными моделями, хотя в наше время бурно развивается научный подход - «синергетическая экономика», - который опирается на существенную нелинейность экономических процессов, исследует время и изменения в нелинейной экономической теории.

В математическом аспекте понятие линейности является важным, поскольку из него следует принцип суперпозиции, означающий, что любая линейная композиция решений (например сумма их) также является решением задачи. Используя принцип суперпозиции, нетрудно, отыскав решение в любом частном случае, построить решение для более общей ситуации. Поэтому о качественных свойствах общего случая можно судить исходя из свойств частного - разница между двумя решениями имеет лишь количественный характер. Итак, в случае линейных моделей отзыв (реакция) объекта на изменение условий пропорционально величине этих изменений.

Для нелинейных явлений, математические модели которых не подчинены принципу суперпозиции, знания применительно к поведению части объекта еще не гарантируют знаний о поведении объекта в целом, а его отклик на изменение условий может качественно зависеть от количественной величины (объемов) этих изменений.

Отметим, что большинство реальных процессов и соответствующих (адекватных) им математических моделей являются нелинейными. Линейные же модели соответствуют достаточно частным случаям и, как правило, используются лишь как первое приближение к действительности. Например, модели популяций сразу же становятся нелинейными, если учитывать, что ограниченность доступных популяции ресурсов необходимо обязательно учитывать. Строя такие модели, считают, что:

1) существует «равновесная» численность популяции N_p, которую может обеспечить окружающая среда (с точки зрения сегодняшнего дня);

2) скорость изменения численности популяции пропорциональна этой численности, умноженной (в отличие от модели Мальтуса) на величину отклонения ее от равновесного значения численности, то есть:

(2.1)

Сомножитель в этом уравнении обеспечивает механизм «насыщения» численности - при N <N_p (N> N_p) скорость роста положительная (отрицательная) и стремится к нулю, если N ® N_p.

Представим уравнение (2.1) в виде:

Интегрируя это уравнение, получим:

Постоянную интегрирования можно получить из условия N (t = 0) =
= N (0), откуда

Таким образом, имеем:

или

Поведение функции N (t) описывается так называемой логистической кривой N (t) (рис. 2.2).

Рис. 2.2. Логистические кривые, соответствующие различным значением начальной численности N(0.)

При любом N(0) численность стремится к равновесному значению N_p и, что характерно, тем медленнее, чем ближе N(t) к N(0). Итак, равновесие, в отличие от классической модели, в данном случае является устойчивым. Отметим, что логистическая модель более реалистично отражает динамику популяции по сравнению с моделью Мальтуса, но сама она в случае необходимости становится нелинейной и поэтому более сложной. Отметим, что предположение о механизмах насыщения используются в формировании ряда моделей различных экономических объектов и процессов как на микро, так и на макроэкономическом уровнях.